备考2024年浙江中考数学一轮复习专题20.1三角形(2) 基础夯实
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 如图,AB=AD , 点B关于AC的对称点E恰好落在CD上.若∠BAD=a(0°<a<180°),则∠ACB的度数为( )
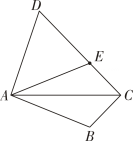 A、45° B、a﹣45° C、a D、90°﹣a2. △DEF和△GHK均为等边三角形,将它们按如图1、图2的方式放置在等边三角形ABC内,若求图1、图2中的阴影部分面积的和,则只需知道( )
A、45° B、a﹣45° C、a D、90°﹣a2. △DEF和△GHK均为等边三角形,将它们按如图1、图2的方式放置在等边三角形ABC内,若求图1、图2中的阴影部分面积的和,则只需知道( ) A、△BDE的面积 B、四边形BEFD的面积 C、△ABC面积 D、△DGH的面积3. 在△ABC中,它的三边分别为a,b,c,下列条件:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A:∠B:∠C=3:4:5;④a:b:c=1::;其中,能确定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个4. 如图1是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8cm(如图2),双翼的边缘AC=BD=60cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A、△BDE的面积 B、四边形BEFD的面积 C、△ABC面积 D、△DGH的面积3. 在△ABC中,它的三边分别为a,b,c,下列条件:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A:∠B:∠C=3:4:5;④a:b:c=1::;其中,能确定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个4. 如图1是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8cm(如图2),双翼的边缘AC=BD=60cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( ) A、60 8 B、60 8 C、64 D、685. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )
A、60 8 B、60 8 C、64 D、685. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )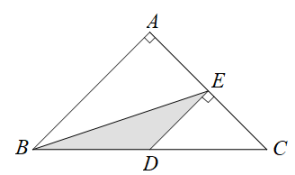 A、3 B、4 C、5 D、66. 下列几组数中,为勾股数的是( )A、 , , 1 B、3,4,6 C、5,12,13 D、0.9,1.2,1.57. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.在如图所示的弦图中,四边形ABCD和EFGH都是正方形,是四个全等的直角三角形.若 , 则正方形ABCD的边长是( )
A、3 B、4 C、5 D、66. 下列几组数中,为勾股数的是( )A、 , , 1 B、3,4,6 C、5,12,13 D、0.9,1.2,1.57. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.在如图所示的弦图中,四边形ABCD和EFGH都是正方形,是四个全等的直角三角形.若 , 则正方形ABCD的边长是( ) A、13 B、28 C、48 D、528. 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
A、13 B、28 C、48 D、528. 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( ) A、cm B、cm C、cm D、7cm9. 如图,在Rt△ABC中,∠A=90°,∠B=30°.动点P从点C出发,沿边CB,BA向点A运动.在点P运动过程中,△PAC可能成为的特殊三角形依次是( )
A、cm B、cm C、cm D、7cm9. 如图,在Rt△ABC中,∠A=90°,∠B=30°.动点P从点C出发,沿边CB,BA向点A运动.在点P运动过程中,△PAC可能成为的特殊三角形依次是( )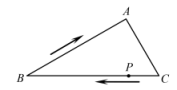 A、直角三角形→等边三角形→直角三角形→等边三角形→直角三角形 B、等腰三角形→直角三角形→等边三角形→直角三角形→等腰直角三角形 C、直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形 D、等腰直角三角形→等腰三角形→直角三角形→等腰直角三角形→直角三角形10. 如图,已知 , AB=4,AC=6,点P在内,将绕着点A逆时针方向旋转60°得到.则AE+PB+PC的最小值为( )
A、直角三角形→等边三角形→直角三角形→等边三角形→直角三角形 B、等腰三角形→直角三角形→等边三角形→直角三角形→等腰直角三角形 C、直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形 D、等腰直角三角形→等腰三角形→直角三角形→等腰直角三角形→直角三角形10. 如图,已知 , AB=4,AC=6,点P在内,将绕着点A逆时针方向旋转60°得到.则AE+PB+PC的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,Rt△ABC中,∠C=90°,AC=8,BC=6.有一动点P从点C开始沿C→B→A方向以2cm/s的速度运动到点A后停止运动,当运动时间为秒时,△ACP是等腰三角形.
 12. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连接OD,当α=°时,△AOD是直角三角形.
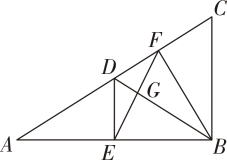
12. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连接OD,当α=°时,△AOD是直角三角形. 13. 如图,在Rt△ABC中,∠ABC=90°,∠A=30°,点D , E , F分别是线段AC , AB , DC的中点,下列结论:①△EFB为等边三角形.②S四边形DFBE=S△ABC . ③AE=2DF . ④AC=8DG . 其中正确的是 .
13. 如图,在Rt△ABC中,∠ABC=90°,∠A=30°,点D , E , F分别是线段AC , AB , DC的中点,下列结论:①△EFB为等边三角形.②S四边形DFBE=S△ABC . ③AE=2DF . ④AC=8DG . 其中正确的是 .
 14. 如图,等腰Rt△ABC的直角边长为 , D,E分别为边AB,AC上两个动点,且AE=BD,则CD+BE的最小值.
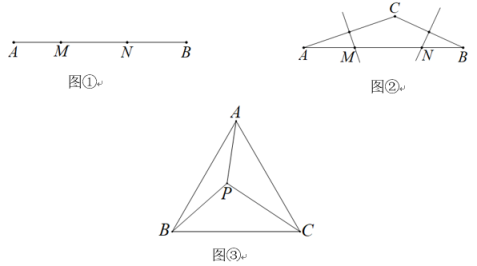
14. 如图,等腰Rt△ABC的直角边长为 , D,E分别为边AB,AC上两个动点,且AE=BD,则CD+BE的最小值.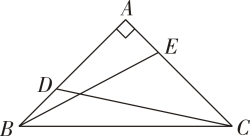 15. 如图所示,中, , , 点沿射线方向从点出发以的速度移动,点沿射线方向从点出发以的速度移动, , 同时出发, 秒后,的面积为.
15. 如图所示,中, , , 点沿射线方向从点出发以的速度移动,点沿射线方向从点出发以的速度移动, , 同时出发, 秒后,的面积为. 16. 如图是一个提供床底收纳支持的气压伸缩杆,除了AB是完全固定的钢架外,AD,BC,DE属于位置可变的定长钢架.如图1所示, , 伸缩杆PQ的两端分别固定在BC,CE两边上,其中.当伸缩杆PQ打开最大时,如图2所示,成 , 此时 , 则可变定长钢架CD的长度为.当伸缩杆完全收拢时, , 则此时床高(CD与AB之间的距离)为cm.
16. 如图是一个提供床底收纳支持的气压伸缩杆,除了AB是完全固定的钢架外,AD,BC,DE属于位置可变的定长钢架.如图1所示, , 伸缩杆PQ的两端分别固定在BC,CE两边上,其中.当伸缩杆PQ打开最大时,如图2所示,成 , 此时 , 则可变定长钢架CD的长度为.当伸缩杆完全收拢时, , 则此时床高(CD与AB之间的距离)为cm.
三、解答题(共5题,共32分)
-
17. 葛藤是一种刁钻的植物.它自己腰托不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是绕树盘旋上升的路段,总是沿着最短路线——盘旋前进的,难道植物也懂得数学吗?阅读以上信息,你能设计一种方法解决下列问题吗?
 (1)、如图,如果树干的周长(即底面圆的周长)为30cm,从点A绕一圈到点B,葛藤升高40cm,则它爬行路程是多少厘米?(2)、如果树干的周长(即底面圆的周长)为40cm,绕一圈爬行50cm,则爬行一圈升高多少厘米?如果爬行10圈到达树顶,则树干高多少厘米?18. 如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒(t≠0).
(1)、如图,如果树干的周长(即底面圆的周长)为30cm,从点A绕一圈到点B,葛藤升高40cm,则它爬行路程是多少厘米?(2)、如果树干的周长(即底面圆的周长)为40cm,绕一圈爬行50cm,则爬行一圈升高多少厘米?如果爬行10圈到达树顶,则树干高多少厘米?18. 如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒(t≠0). (1)、出发2秒后,求PQ的长;(2)、出发几秒钟后,直线PQ把△ABC的周长分成1:2的两部分;(3)、在点Q的运动过程中,是否存在时间t求能使△BCQ成为等腰三角形,如果有,请求出t,如果没有请说明理由.19. 如图,在△ABC中, , ∠ACB=90°,点P是边AB所在直线上的一个动点,连结CP , 将CP绕点C按逆时针方向旋转90°得到CD , 连结AD .
(1)、出发2秒后,求PQ的长;(2)、出发几秒钟后,直线PQ把△ABC的周长分成1:2的两部分;(3)、在点Q的运动过程中,是否存在时间t求能使△BCQ成为等腰三角形,如果有,请求出t,如果没有请说明理由.19. 如图,在△ABC中, , ∠ACB=90°,点P是边AB所在直线上的一个动点,连结CP , 将CP绕点C按逆时针方向旋转90°得到CD , 连结AD . (1)、如图1,当点P在AB的延长线上时,求证:AD⊥AB .(2)、如图2,若点P从点B运动到点A .
(1)、如图1,当点P在AB的延长线上时,求证:AD⊥AB .(2)、如图2,若点P从点B运动到点A .①△DPA的周长是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
②如图3,过点B作BA的垂线,与直线DC交于点N , 作点B关于直线DC的对称点Q , 直线NQ交直线直线AD于点M , 若∠NMD=60°,求BP的长.
20. 有两块腰长为的等腰直角白铁皮. (1)、按图1裁出一块正方形 , 四个顶点都在边上.求裁出正方形的边长.(2)、按图2裁出面积总和为的两块矩形铁皮,裁剪过程如下:
(1)、按图1裁出一块正方形 , 四个顶点都在边上.求裁出正方形的边长.(2)、按图2裁出面积总和为的两块矩形铁皮,裁剪过程如下:步骤1:在等腰直角白铁皮上裁下一块长宽不等的矩形 , 矩形的四个顶点都在的边上,留下两块等腰直角三角形零料,分别记为 , .
步骤2:取其中一块零料 , 从零料上裁下一块正方形 ,正方形的四个顶点都在零料边上.求裁下的正方形边长.
21. 如图,直线 , 一副三角尺按如图放置,其中点在直线上,点 , 均在直线上,且平分 . (1)、求的度数.(2)、如图 , 若将三角形绕点以每秒度的速度按逆时针方向旋转的对应点分别为 , , 设旋转时间为 .
(1)、求的度数.(2)、如图 , 若将三角形绕点以每秒度的速度按逆时针方向旋转的对应点分别为 , , 设旋转时间为 .在旋转过程中,若边 , 求的值.
若在三角形绕点旋转的同时,三角形绕点以每秒度的速度按顺时针方向旋转的对应点为 , 请直接写出当边时的值.
四、实践探究题(共5题,共40分)
-
22. 定义:若以三条线段 , , 为边能构成一个直角三角形,则称线段 , , 是勾股线段组.
 (1)、如图①,已知点M,N是线段AB上的点,线段AM,MN,NB是勾股线段组.若AB=12,AM=3,求MN的长;(2)、如图②,△ABC中,∠A=17°,∠B=28°,边AC,BC的垂直平分线分别交AB于点M,N,求证:线段AM,MN,NB是勾股线段组;(3)、如图③,在等边△ABC,P为△ABC内一点,线段AP,BP,CP构成勾股线段组,CP为此线段组的最长线段,求∠APB的度数.23. 定义:如果三角形有两个内角的差为60°,那么这样的三角形叫做“准等边三角形”.
(1)、如图①,已知点M,N是线段AB上的点,线段AM,MN,NB是勾股线段组.若AB=12,AM=3,求MN的长;(2)、如图②,△ABC中,∠A=17°,∠B=28°,边AC,BC的垂直平分线分别交AB于点M,N,求证:线段AM,MN,NB是勾股线段组;(3)、如图③,在等边△ABC,P为△ABC内一点,线段AP,BP,CP构成勾股线段组,CP为此线段组的最长线段,求∠APB的度数.23. 定义:如果三角形有两个内角的差为60°,那么这样的三角形叫做“准等边三角形”.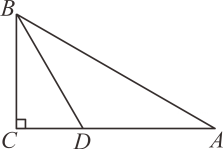 (1)、顶角为120°的等腰三角形(填“是”或“不是”)“准等边三角形”.(2)、已知△ABC是“准等边三角形”,其中∠A=35°,∠C>90°,求∠B的度数.(3)、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+ , 点D在AC边上,若△BCD是“准等边三角形”,求BD的长.24. 阅读材料:
(1)、顶角为120°的等腰三角形(填“是”或“不是”)“准等边三角形”.(2)、已知△ABC是“准等边三角形”,其中∠A=35°,∠C>90°,求∠B的度数.(3)、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+ , 点D在AC边上,若△BCD是“准等边三角形”,求BD的长.24. 阅读材料:⑴对于任意两个数a、b的大小比较,有下面的方法:
当a﹣b>0时,一定有a>b;
当a﹣b=0时,一定有a=b;
当a﹣b<0时,一定有a<b .
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
⑵对于比较两个正数a、b的大小时,我们还可以用它们的平方进行比较:
∵a2﹣b2=(a+b)(a﹣b),a+b>0
∴(a2﹣b2)与(a﹣b)的符号相同
当a2﹣b2>0时,a﹣b>0,得a>b
当a2﹣b2=0时,a﹣b=0,得a=b
当a2﹣b2<0时,a﹣b<0,得a<b
解决下列实际问题:
(1)、课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x , 每张B5纸的面积为y,且x>y , 张丽同学的用纸总面积为W1 , 李明同学的用纸总面积为W2 . 回答下列问题:①W1= 用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)、如图1所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,已知A、B到l的距离分别是3km、4km(即AC=3km , BE=4km),AB=xkm , 现设计两种方案:
方案一:如图2所示,AP⊥l于点P , 泵站修建在点P处,该方案中管道长度a1=AB+AP .
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P , 泵站修建在店P处,该方案中管道长度a2=AP+BP .
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
25. (1)、【思维启迪】
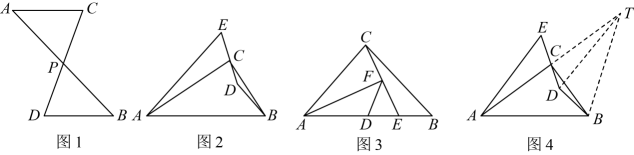
(1)、【思维启迪】如图1,点P是线段 , 的中点,则与的数量关系为 , 位置关系为;
(2)、【思维探索】如图2,在中, , 点D为内一点,连接 , , 延长到点E , 使 , 连接 , 若 , 请用等式表示 , , 之间的数量关系,并说明理由;
★小明思考良久后,根据这一条件,给出了如图4的辅助线:延长到T , 使得 , 连接 , , 请你根据小明给出的辅助线,继续猜想 , , 之间的数量关系,并说明理由.
(3)、如图3,在中, , , 点D为中点,点E在线段上(点E不与点B , 点D重合),连接 , 过点A作 , 连接 , 若 , , 请求出的长.26. 【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,AD是△ABC的中线,若AB=5,AC=3,求AD的取值范围.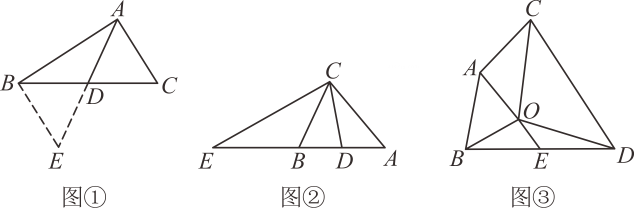 (1)、【探究方法】
(1)、【探究方法】小强所在的小组通过探究发现,延长AD至点E使ED=AD,连接BE.
可以证出△ADC≌△EDB,利用全等三角形的性质可将已知的边长与AD转化到到△ABE中,进而求出AD的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线AD延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
请你利用上面解答问题的思路方法,求出求AD的取值范围的过程.
(2)、【问题解决】如图②,CB是△AEC的中线,CD是△ABC的中线,且AB=AC,下列四个选项中:A.AC=BE B.CE=2CD C.∠BCD=∠BCE D.∠ACD=∠BCD.直接写出所有正确选项的序号是.
(3)、【问题拓展】如图③,在△ABO和△CDO中,OA=OB,OC=OD,∠AOB与∠COD互补,连接AC、BD,E是BD的中点,求证:OE=AC.