备考2024年浙江中考数学一轮复习专题19.1三角形(1) 基础夯实
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 三个内角的度数之比为3:4:5,那么是( )A、等腰三角形 B、锐角三角形 C、钝角三角形 D、直角三角形2. 如图,M,A,N是直线l上的三点,AM=3 , AN=5, P是直线l外一点,且∠PAN=60°, AP=1, 若动点Q从点M出发,向点N移动,移动到点N停止,在△APQ形状的变化过程中,依次出现的特殊三角形是( )
 A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形3. 如图,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列结论中①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④EF平分∠AEC,⑤BE+DF=EF.其中正确的结论是( )
A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形3. 如图,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列结论中①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④EF平分∠AEC,⑤BE+DF=EF.其中正确的结论是( )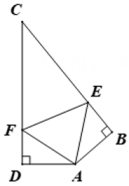 A、④⑤ B、①② C、③⑤ D、①②③4. 如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B , ∠B=4∠DAE , 那么∠C的度数为( )
A、④⑤ B、①② C、③⑤ D、①②③4. 如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B , ∠B=4∠DAE , 那么∠C的度数为( ) A、75° B、72° C、70° D、60°5. 将长方形纸片ABCD如图折叠,B , C两点恰好重合在AD边上的同一点P处,折痕分别是MH , NG , 若∠MPN=90°,PM=3,MN=5,分别记△PHM , △PNG , △PMN的面积为S1 , S2 , S3 , 则S1 , S2 , S3之间的数量关系是( )
A、75° B、72° C、70° D、60°5. 将长方形纸片ABCD如图折叠,B , C两点恰好重合在AD边上的同一点P处,折痕分别是MH , NG , 若∠MPN=90°,PM=3,MN=5,分别记△PHM , △PNG , △PMN的面积为S1 , S2 , S3 , 则S1 , S2 , S3之间的数量关系是( )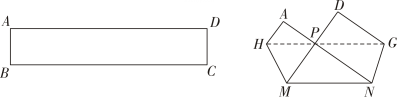 A、S3=S1+S2 B、3S3=2S1+2S2 C、S3=5S2-5S1 D、2S3=3S2-S16. 一个三角形的三个内角中,至少有( )A、一个锐角 B、两个锐角 C、一个钝角 D、一个直角7. 一个图形经过下列变换后得到新图形,不能全等的是( )A、平移 B、翻折 C、旋转 D、缩小8. 如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于( )
A、S3=S1+S2 B、3S3=2S1+2S2 C、S3=5S2-5S1 D、2S3=3S2-S16. 一个三角形的三个内角中,至少有( )A、一个锐角 B、两个锐角 C、一个钝角 D、一个直角7. 一个图形经过下列变换后得到新图形,不能全等的是( )A、平移 B、翻折 C、旋转 D、缩小8. 如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于( )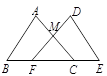 A、2∠B B、2∠ACB C、∠A+∠D D、∠B+∠ACB9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )
A、2∠B B、2∠ACB C、∠A+∠D D、∠B+∠ACB9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )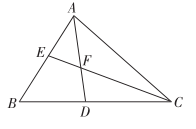
①;②;③若 , 则;④ .
A、1个 B、2个 C、3个 D、4个10. 如图,要测量池塘两岸相对的两点 , 间的距离,小明在池塘外取的垂线上的点 , , 使 . 再画出的垂线 , 使与 , 在一条直线上,这时测得的长就是的长.依据是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 已知三角形三条边分别为a+4,a+5,a+6,则a的取值范围是 .12. 如图,AD、CE是△ABC的中线,若△CDG的面积是1,则△ABC的面积为 .
 13. 造房子时屋顶常用三角结构,从数学角度来看,是应用了 ;而活动挂架则用了四边形的 .14. 一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 . (填序号)
13. 造房子时屋顶常用三角结构,从数学角度来看,是应用了 ;而活动挂架则用了四边形的 .14. 一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 . (填序号) 15. 如图,在边长为6的等边△ABC中,点E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为 .
15. 如图,在边长为6的等边△ABC中,点E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为 . 16. 如图, , , 添加一个条件 , 使得 .
16. 如图, , , 添加一个条件 , 使得 .
三、作图题(共6分)
-
17. 如图,在△ABC中,∠C=90°.
 (1)、点D在边AC上,且点D到∠B两边的距离相等,用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上清楚地标注点D);(2)、在第(1)题的条件下,如果BC=12,AC=5 ,求的值.
(1)、点D在边AC上,且点D到∠B两边的距离相等,用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上清楚地标注点D);(2)、在第(1)题的条件下,如果BC=12,AC=5 ,求的值.四、解答题(共6题,共48分)
-
18.
如图,△ABC中,AB=AC,∠C=70°,作AB的垂直平分线交AB于E,交AC于D,求∠DBC的度数.
 19. 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.
19. 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.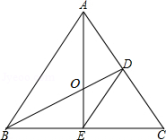 (1)、判断△CDE的形状,并说明理由.(2)、若AO=12,求OE的长.20. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,E,F分别是直线AC,AB上的动点,连结EF.
(1)、判断△CDE的形状,并说明理由.(2)、若AO=12,求OE的长.20. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,E,F分别是直线AC,AB上的动点,连结EF. (1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.21. 在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.
(1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.21. 在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB. (1)、求证:CD平分∠MCH;(2)、过点M作AB的垂线交CD的延长线于点E,
(1)、求证:CD平分∠MCH;(2)、过点M作AB的垂线交CD的延长线于点E,①求证:CM=EM;
②△AEM是什么三角形?证明你的猜想.
22. 小明利用一根3m长的竿子来测量路灯的高度.他的方法是这样的:在路灯前选一点 , 使m,并测得 , 然后把竖直的竿子(m)在的延长线上移动,使 , 此时量得m.根据这些数据,小明计算出了路灯的高度.你知道小明计算的路灯的高度是多少?为什么? 23. 将一副直角三角板和如图(1)放置,此时四点在同一条直线上,点A在边上,其中 , , .
23. 将一副直角三角板和如图(1)放置,此时四点在同一条直线上,点A在边上,其中 , , . (1)、求的度数;(2)、将图(1)中的三角板绕点A以每秒的速度,按顺时针方向旋转一定的角度后,记为三角板 , 设旋转的时间为t秒.
(1)、求的度数;(2)、将图(1)中的三角板绕点A以每秒的速度,按顺时针方向旋转一定的角度后,记为三角板 , 设旋转的时间为t秒.①当旋转至图(2)时,此时 , 求a的值;
②若在旋转过程中,三角板的某一边恰好与所在的直线平行,直接写出t的值.
五、实践探究题(共2题,共18分)
-
24.
 (1)、【问题发现】
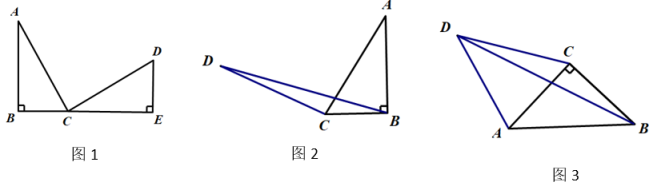
(1)、【问题发现】如图1,在△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=4,ED=3,则BE=.
(2)、【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=3,过点C作CD⊥AC,且CD=AC,求△BCD的面积.
(3)、【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为14且CD的长为7,求△BCD的面积.
25. 如图 (1)、如图1,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A,B,C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中;你发现线段AD与BE有什么数量关系?试说明你的结论(2)、【变式探究】如图2,在△ABC中,点D、E、F分别在边BC、AB、AC上,若∠B=∠FDE=∠C,那么∠BED与∠CDF有何关系,并加以说理;(3)、【拓展应用】如图3,在△ABC中,BA=BC,∠B=45°,点D、F分别是边BC、AB上的动点,且AF=2BD,以DF为腰向右做等腰△DEF,使得DE=DF,∠EDF=45°, 连接CE.
(1)、如图1,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A,B,C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中;你发现线段AD与BE有什么数量关系?试说明你的结论(2)、【变式探究】如图2,在△ABC中,点D、E、F分别在边BC、AB、AC上,若∠B=∠FDE=∠C,那么∠BED与∠CDF有何关系,并加以说理;(3)、【拓展应用】如图3,在△ABC中,BA=BC,∠B=45°,点D、F分别是边BC、AB上的动点,且AF=2BD,以DF为腰向右做等腰△DEF,使得DE=DF,∠EDF=45°, 连接CE.①试判断线段DC、BD、BF之间的数量关系,并说明理由;
②如图4,已知AC=2,点G是AC的中点,连接EA,EG,直接写出EA+EG的最小值.
-