备考2024年浙江中考数学一轮复习专题19.1三角形(1) 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
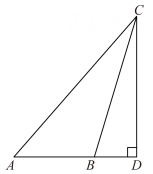 A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线2. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、83. 用尺规作一个角的角平分线,下列作法中错误的是( )A、
A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线2. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、83. 用尺规作一个角的角平分线,下列作法中错误的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知 ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
4. 已知 ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A、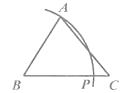 B、
B、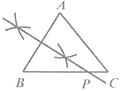 C、
C、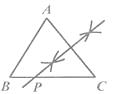 D、
D、 5. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
5. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )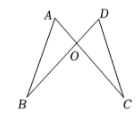 A、SSS B、SAS C、AAS D、HL6.
A、SSS B、SAS C、AAS D、HL6.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
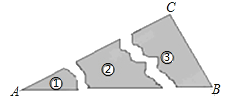 A、带①去 B、带②去 C、带③去 D、①②③都带去7. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
A、带①去 B、带②去 C、带③去 D、①②③都带去7. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ). A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 如图,在三角形ABC中,AB=11,AC=15,点M是BC的中点,AD是∠BAC的角平分线,MF∥AD,则FC=( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 如图,在三角形ABC中,AB=11,AC=15,点M是BC的中点,AD是∠BAC的角平分线,MF∥AD,则FC=( ) A、14 B、13 C、12 D、119. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( )
A、14 B、13 C、12 D、119. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( ) A、 B、 C、 D、10. 如图,点P,Q,R分别在等边△ABC的三边上,且AP=BQ=CR,过点P,Q,R分别作BC,CA,AB边的垂线,得到△DEF.若要求△DEF的面积,则只需知道( )
A、 B、 C、 D、10. 如图,点P,Q,R分别在等边△ABC的三边上,且AP=BQ=CR,过点P,Q,R分别作BC,CA,AB边的垂线,得到△DEF.若要求△DEF的面积,则只需知道( ) A、AB的长 B、AP的长 C、BP的长 D、DP的长
A、AB的长 B、AP的长 C、BP的长 D、DP的长二、填空题(每题3分,共24分)
-
11. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 .
 12. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。
12. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。 13. 已知 中, ,在同一平面内,若 ,则 的长为 .14. 在中, , 分别以A,B为圆心,大于线段长度一半的长为半径作弧,相交于点M,N,作直线 , 交直线于点D,点D恰好满足 , 则的度数是.15. 如图,在平面直角坐标系中, , ,P是x轴上动点,连结 ,将线段 绕点A逆时针旋转 得到线段 ,连结 ,取 中点为M. 的度数为 , 的最小值为.
13. 已知 中, ,在同一平面内,若 ,则 的长为 .14. 在中, , 分别以A,B为圆心,大于线段长度一半的长为半径作弧,相交于点M,N,作直线 , 交直线于点D,点D恰好满足 , 则的度数是.15. 如图,在平面直角坐标系中, , ,P是x轴上动点,连结 ,将线段 绕点A逆时针旋转 得到线段 ,连结 ,取 中点为M. 的度数为 , 的最小值为. 16. 已知△ABC中,∠BAC=90°,∠B=30°.用尺规画出射线AP(痕迹如图),则∠APB的度数为.
16. 已知△ABC中,∠BAC=90°,∠B=30°.用尺规画出射线AP(痕迹如图),则∠APB的度数为. 17. 如图,在△ABC中,AB=AC,∠A=36°,分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,再以点B为圆心,BC长为半径作弧,交直线MN于点E,则∠BEC的度数为.
17. 如图,在△ABC中,AB=AC,∠A=36°,分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,再以点B为圆心,BC长为半径作弧,交直线MN于点E,则∠BEC的度数为. 18. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 .
18. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 .
三、作图题(共10分)
-
19. 如图,为制作角度尺,将长为10,宽为4的矩形OABC分割成4×10的小正方形网格.在该矩形边上取点P,来表示∠POA的度数.阅读以下作图过程,并回答下列问题:
作法(如图)
结论
①在上取点 , 使.
,
点表示.
②以为圆心,8为半径作弧,与交于点
,
点表示.
③分别以 , 为圆心,大于长度一半的长为半径作弧,相交于点E,F,连结EF与BC相交于点.
…
④以为圆心,的长为半径作弧,与射线交于点 , 连结交于点.
…
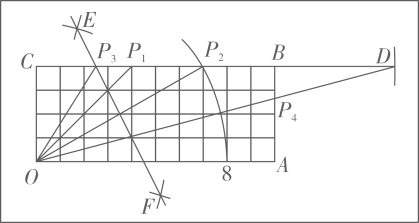 (1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).
(1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).四、解答题(共4题,共36分)
-
20. 已知:如图,在和中,在同一条直线上.下面四个条件:
①②;③;④
 (1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.21. 如图,是等边三角形,D是边AB上一点,以CD为边作E等边 , DE交AC于点F,连接AE,
(1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.21. 如图,是等边三角形,D是边AB上一点,以CD为边作E等边 , DE交AC于点F,连接AE,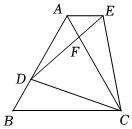 (1)、求证:≌(2)、若 , , 求CD的长.22. 问题:如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC。若∠BAE=90°,∠B=45°,求∠DAC的度数。
(1)、求证:≌(2)、若 , , 求CD的长.22. 问题:如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC。若∠BAE=90°,∠B=45°,求∠DAC的度数。答案:∠DAC=45°。
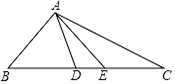
思考:
(1)、如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由。(2)、如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数。23. 如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D , 交OA于点E , 连结OB .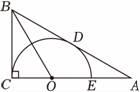 (1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.
(1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.五、实践探究题(共2题,共20分)
-
24.
 (1)、【提出问题】
(1)、【提出问题】如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)、【类比探究】如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)、【拓展延伸】如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
25.(1)、【阅读材料】如图①,四边形ABCD中, , 点E,F分别在上,若 , 求证:.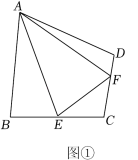 (2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)
(2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)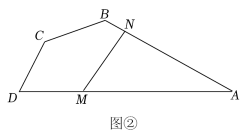
-