备考2024年浙江中考数学一轮复习专题18.1相交线与平行线 基础夯实
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 在同一平面内,有a,b,c三条直线,若a与b不平行,b与c不平行,则下列判断中,正确的是( )A、a与c一定平行 B、a与c一定不平行 C、a与c一定垂直 D、a与c可能相交,也可能平行2. 同一平面内互不重合的3条直线的交点的个数是( )A、可能是0,1,2 B、可能是0,2,3 C、可能是0,1,2或3 D、可能是1,可能是33. 下列图形中,与互为内错角的是( )A、
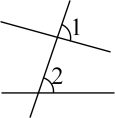 B、
B、 C、
C、 D、
D、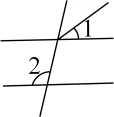 4. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、
4. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、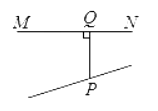 B、
B、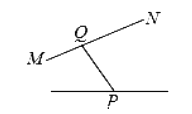 C、
C、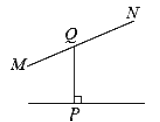 D、
D、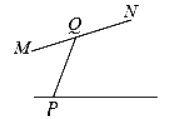 5. 如图,∠AOB的一边OA为一面平面镜,∠AOB=37°36',在OB上有一点E,从点E射出一束光线,经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
5. 如图,∠AOB的一边OA为一面平面镜,∠AOB=37°36',在OB上有一点E,从点E射出一束光线,经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( ) A、75°36' B、75°12' C、74°36' D、74°12'6. 如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )
A、75°36' B、75°12' C、74°36' D、74°12'6. 如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( ) A、∠1=∠2 B、∠3=∠4 C、∠2+∠4=180° D、∠1+∠4=180°7. 如图, , 平分 , 的反向延长线交的平分线于点M,则与的数量关系是( )
A、∠1=∠2 B、∠3=∠4 C、∠2+∠4=180° D、∠1+∠4=180°7. 如图, , 平分 , 的反向延长线交的平分线于点M,则与的数量关系是( ) A、 B、 C、 D、8. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、49. 要得知作业纸上两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图):
A、 B、 C、 D、8. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、49. 要得知作业纸上两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图):方案Ⅰ

1.作一直线EF,交AB,CD于点E,F;
2.测量∠AEF和∠CFE的大小;
3.计算180°-∠AEF-∠CFE即可.
方案Ⅱ

1.作一直线EF,交AB,CD于点E,F;
2.摆放三角板,使两直角边恰分别过点E,F;
3.测量∠AEG和∠CFG的大小;
4.计算90°-∠AEG-∠CFG即可.
关于方案Ⅰ、Ⅱ的可行性,下列选项正确的是( )
A、Ⅰ、Ⅱ都可行 B、Ⅰ可行、Ⅱ不可行 C、Ⅰ不可行、Ⅱ可行 D、Ⅰ、Ⅱ都不可行10. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )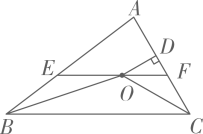 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共20分)
-
11. 如图,直线l截直线a,b所得的同位角有对,它们是;内错角有对,它们是;同旁内角有对,它们是;对顶角有对,它们是.
 12. 下列说法正确的有(填序号):.
12. 下列说法正确的有(填序号):.①同位角相等;
②在同一平面内,两条不相交的线段是平行线;
③在同一平面内,如果a//b,b//c,则a//c;
④在同一平面内,过直线外一点有且只有一条直线与已知直线平行.
13. 将一副三角尺和一张对边平行的纸条按如图所示的方式摆放,两块三角尺的一条直角边重合,含30°角的三角尺的斜边与纸条的一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是 14. 如图,直线AB,CD交于点O,∠AOC:∠COE=1:2.若∠BOD=28°,则∠COE等于度.
14. 如图,直线AB,CD交于点O,∠AOC:∠COE=1:2.若∠BOD=28°,则∠COE等于度.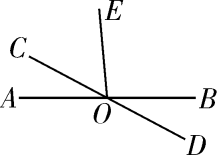 15. 如图消防云梯,其示意图如图1所示,其由救援台AB,延展臂BC(B在C的左侧)、伸展主臂CD,支撑臂EF构成,在作业过程中,救援台AB、车身GH及地面MN三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂BC与支摚臂EF所在直线互相垂直,且∠EFH=69°,则这时展角∠ABC= .
15. 如图消防云梯,其示意图如图1所示,其由救援台AB,延展臂BC(B在C的左侧)、伸展主臂CD,支撑臂EF构成,在作业过程中,救援台AB、车身GH及地面MN三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂BC与支摚臂EF所在直线互相垂直,且∠EFH=69°,则这时展角∠ABC= .
三、作图题(共2题,共12分)
-
16. 图①,②,③均为4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的端点均在格点上.(要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法)
 (1)、在图①中画出一条格点线段MN , 使MN∥AB .(2)、在图②中画出格点线段GH , 使GH⊥AB且GH=AB .(3)、在图③中作出AB的三等分点.17. 如图所示,已知直线l表示一段公路,点A表示学校,点B表示书店,点C表示市图书馆.
(1)、在图①中画出一条格点线段MN , 使MN∥AB .(2)、在图②中画出格点线段GH , 使GH⊥AB且GH=AB .(3)、在图③中作出AB的三等分点.17. 如图所示,已知直线l表示一段公路,点A表示学校,点B表示书店,点C表示市图书馆.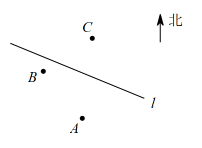 (1)、请画出学校A到书店B的最短路线.(2)、在公路l上找一个路口M , 使得AM+CM的值最小.(3)、现要从学校A向公路l修一条小路AD , 怎样修路才能使小路AD的长最短?请画出小路AD的路线,并说明作图依据.
(1)、请画出学校A到书店B的最短路线.(2)、在公路l上找一个路口M , 使得AM+CM的值最小.(3)、现要从学校A向公路l修一条小路AD , 怎样修路才能使小路AD的长最短?请画出小路AD的路线,并说明作图依据.四、解答题(共3题,共22分)
-
18. 如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
 19. 如图1,已知AC∥BD,点P是直线AC,BD间的一点,连结AB,AP,BP,过点P作直线MN∥AC.
19. 如图1,已知AC∥BD,点P是直线AC,BD间的一点,连结AB,AP,BP,过点P作直线MN∥AC. (1)、MN与BD的位置关系是什么?请说明理由.(2)、试说明∠APB=∠PBD+∠PA C.(3)、如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.20. 一副直角三角尺叠放如图1所示,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转∠α(∠α=∠BAD且0°<∠α<180°),使两块三角尺至少有一组边平行.
(1)、MN与BD的位置关系是什么?请说明理由.(2)、试说明∠APB=∠PBD+∠PA C.(3)、如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.20. 一副直角三角尺叠放如图1所示,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转∠α(∠α=∠BAD且0°<∠α<180°),使两块三角尺至少有一组边平行. (1)、如图2,当∠α=时,BC∥DE.(2)、请你分别在图3,图4的指定图上,各画一种符合要求的图形,标出∠α,并完成填空:
(1)、如图2,当∠α=时,BC∥DE.(2)、请你分别在图3,图4的指定图上,各画一种符合要求的图形,标出∠α,并完成填空:图3中,当∠α=时,∥;
图4中,当∠α=时,∥.
五、实践探究题(共4题,共36分)
-
21. 已知:如图是一个跳棋棋盘,游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角。跳动时,每-步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始角∠1跳到终点角∠3写出其中两种不同路径,
路径1:∠1∠9∠3.
路径2:∠1∠12∠6∠10∠3.

试一试:
(1)、从起始角∠1跳到终点角∠8;(2)、从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8?22. 小明完成暑假作业后在家复习,他看到七下课本12页例4:“如图1﹣13,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°.判断AB,CD是否平行,并说明理由.”,试着“玩”起数学来: (1)、【基础巩固】
(1)、【基础巩固】
条件和结论互换,改成了:“如图1﹣13,AP平分∠BAC,CP平分∠ACD,AB∥CD,则∠1+∠2=90°.”小明认为这个结论正确.你赞同他的想法吗?请说明理由.(2)、【尝试探究】
小明发现:若将其中一条角平分线改成AC的垂线,则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究:如图1,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2是CP与CD的夹角,
①若∠2=22°,求∠1的度数;
②试说明:2∠1﹣∠2=90°.
(3)、【拓展提高】
如图2,若AB∥CD,AP⊥AC,CP平分∠ACD,请直接写出∠1与∠2的等量关系.23. [感知]:如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:解:如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
 (1)、[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.(2)、[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.24. 【学习新知】射到平面镜上的光线入射光线和反射后的光线反射光线与平面镜所夹的角相等,如图1,是平面镜,若入射光线与水平镜面夹角为 , 反射光线与水平镜面夹角为 , 则 .
(1)、[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.(2)、[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.24. 【学习新知】射到平面镜上的光线入射光线和反射后的光线反射光线与平面镜所夹的角相等,如图1,是平面镜,若入射光线与水平镜面夹角为 , 反射光线与水平镜面夹角为 , 则 .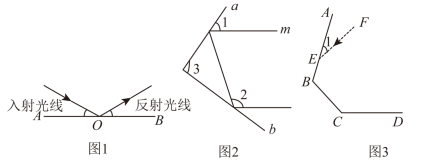 (1)、【初步应用】如图,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、【猜想验证】由(1),请你猜想:当两平面镜、的夹角 ▲ 时,可以使任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,请说明理由;(3)、【拓展探究】如图 , 有三块平面镜 , , , 入射光线与镜面的夹角 , 镜面、的夹角 , 已知入射光线从镜面开始反射,经过为正整数,次反射,当第次反射光线与入射光线平行时,请直接写出的度数.可用含有的代数式表示)
(1)、【初步应用】如图,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、【猜想验证】由(1),请你猜想:当两平面镜、的夹角 ▲ 时,可以使任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,请说明理由;(3)、【拓展探究】如图 , 有三块平面镜 , , , 入射光线与镜面的夹角 , 镜面、的夹角 , 已知入射光线从镜面开始反射,经过为正整数,次反射,当第次反射光线与入射光线平行时,请直接写出的度数.可用含有的代数式表示)