备考2024年浙江中考数学一轮复习专题18.2相交线与平行线 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共36分)
-
1. 如图,过直线外的点P作直线的平行线,下列作法错误的是( )
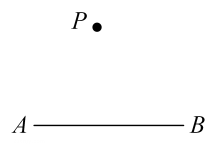 A、
A、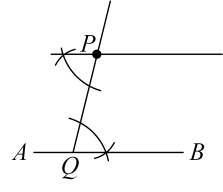 B、
B、 C、
C、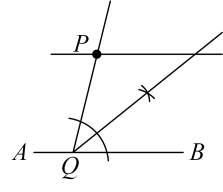 D、
D、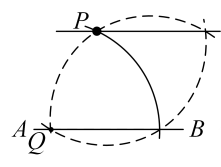 2. 如图:已知∠1=77°,∠2=103°,∠3=77°,则∠4的度数是( )
2. 如图:已知∠1=77°,∠2=103°,∠3=77°,则∠4的度数是( )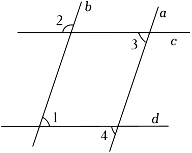 A、75° B、76° C、77° D、103°3. 如图,已知 , 则的度数是( )
A、75° B、76° C、77° D、103°3. 如图,已知 , 则的度数是( )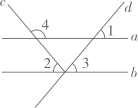 A、 B、 C、 D、4. 如图,把一块三角板 ABC 的直角顶点B放在直线 EF 上, ∠C=30° ,AC∥EF,则 ∠1= ( )
A、 B、 C、 D、4. 如图,把一块三角板 ABC 的直角顶点B放在直线 EF 上, ∠C=30° ,AC∥EF,则 ∠1= ( )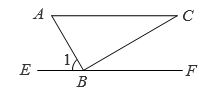 A、30° B、45° C、60° D、75°5. 如图,已知∠1=90° ,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A、30° B、45° C、60° D、75°5. 如图,已知∠1=90° ,为保证两条铁轨平行,添加的下列条件中,正确的是( )
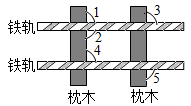 A、 B、 C、 D、6. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )
A、 B、 C、 D、6. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )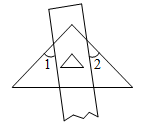 A、40° B、43° C、45° D、47°7. 某同学的作业如下框,其中※处填的依据是( )
A、40° B、43° C、45° D、47°7. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
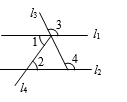 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补8. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补8. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )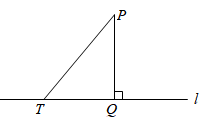 A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ9. 如图,AB∥CD , AF交CD于点E , ∠B=70°,则∠DEF的度数是( )
A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ9. 如图,AB∥CD , AF交CD于点E , ∠B=70°,则∠DEF的度数是( )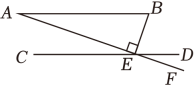 A、10° B、20° C、30° D、40°10. 点A为直线外一点,于点C, . 点P是直线上的动点,则线段长可能是( )A、1 B、3 C、5 D、711. 如图是一款教室护眼灯 , 用两根电线 , 吊在天花板上,已知 , 为保证护眼灯与天花板平行,添加下列条件中,正确的是( )
A、10° B、20° C、30° D、40°10. 点A为直线外一点,于点C, . 点P是直线上的动点,则线段长可能是( )A、1 B、3 C、5 D、711. 如图是一款教室护眼灯 , 用两根电线 , 吊在天花板上,已知 , 为保证护眼灯与天花板平行,添加下列条件中,正确的是( )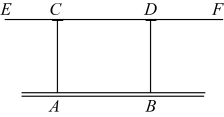 A、 B、 C、 D、12. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).
A、 B、 C、 D、12. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).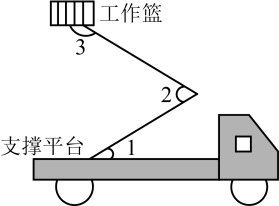 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共21分)
-
13. 如图,一条公路经两次转弯后,方向未变.第一次的拐角是 , 第二次的拐角是°.
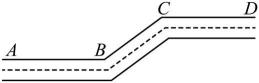 14. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
14. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .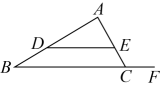 15. 根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为 , 光线n与光线k的夹角的度数为.则x与y之间的数量关系是.
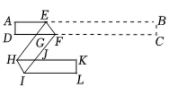
15. 根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为 , 光线n与光线k的夹角的度数为.则x与y之间的数量关系是. 16. 如图, 矩形纸条 中, , 把该纸条依次沿着互相平行的两条直线 , HI对折得到“ "形图案. 已知 , 要使点 , 点 分别在 和 的延长线上(不与 重合), 则 ; 的取值范围是.
16. 如图, 矩形纸条 中, , 把该纸条依次沿着互相平行的两条直线 , HI对折得到“ "形图案. 已知 , 要使点 , 点 分别在 和 的延长线上(不与 重合), 则 ; 的取值范围是.
 17. 小明利用折射定律 , ( , 为折射率,为入射角,为折射角)制作了一个测算液体折射率的装置.光线从点A按固定角度从空气射入液面,通过调节液面高度,使光线折射后恰好落到点C.已知 , 空气折射率为1,正方形ABCD的边长为36cm.如图1装入某款家用食用油时,恰好CF=15cm,该食用油的折射率为.如图2装入纯净水时,水的折射率为 , 通过度量CF=20cm(存在误差),问此次度量的误差为cm.
17. 小明利用折射定律 , ( , 为折射率,为入射角,为折射角)制作了一个测算液体折射率的装置.光线从点A按固定角度从空气射入液面,通过调节液面高度,使光线折射后恰好落到点C.已知 , 空气折射率为1,正方形ABCD的边长为36cm.如图1装入某款家用食用油时,恰好CF=15cm,该食用油的折射率为.如图2装入纯净水时,水的折射率为 , 通过度量CF=20cm(存在误差),问此次度量的误差为cm.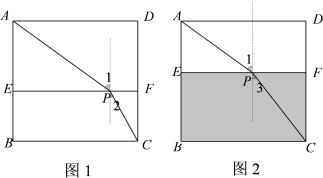 18. 纸带沿AB折叠的三种方法如图所示,有以下结论:①如图1,展开后测得∠1=∠2;②如图2,展开后测得∠1=∠2且∠3=∠4;③如图3,测得∠1=∠2.其中能判定纸带两条边a,b互相平行的是.(填序号).
18. 纸带沿AB折叠的三种方法如图所示,有以下结论:①如图1,展开后测得∠1=∠2;②如图2,展开后测得∠1=∠2且∠3=∠4;③如图3,测得∠1=∠2.其中能判定纸带两条边a,b互相平行的是.(填序号). 19. 图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m,EB=8m,EB'=8 m,在点A观测点F的仰角为45°
19. 图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m,EB=8m,EB'=8 m,在点A观测点F的仰角为45°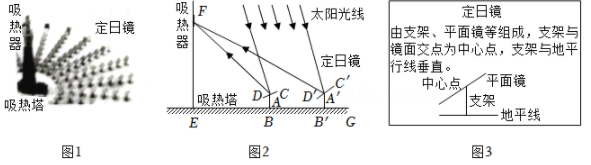 (1)、点F的高度EF为m.(2)、设∠DAB=α,∠D'A'B'=β,则α与β的数量关系是.
(1)、点F的高度EF为m.(2)、设∠DAB=α,∠D'A'B'=β,则α与β的数量关系是.三、作图题(共6分)
-
20. 如图,在4×5的正方形网格中,每个小正方形的边长为1,点A、B在格点上,点C是线段AB与格线的交点.利用网格和无刻度的直尺按下列要求画图.
 (1)、在图1中,过点B作AB的垂线.(2)、在图2中,过点C作AB的垂线.
(1)、在图1中,过点B作AB的垂线.(2)、在图2中,过点C作AB的垂线.四、解答题(共5题,共37分)
-
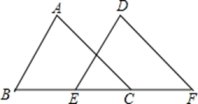
21. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
 22. 如图, 是 的角平分线,在 上取点 ,使 .
22. 如图, 是 的角平分线,在 上取点 ,使 .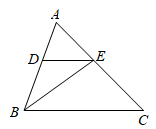 (1)、求证: .(2)、若 , ,求 的度数.23. 如图,已知 , , .
(1)、求证: .(2)、若 , ,求 的度数.23. 如图,已知 , , .

求证:
(1)、 ;(2)、 .24. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.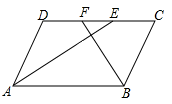
答案: .
(1)、探究:把“问题”中的条件“ ”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求 的值.25. 如图,为的直径,A为上一点,作的平分线交于点D,过点D作的切线,交的延长线于点E.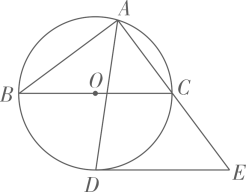 (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.五、实践探究题(共2题,共20分)
-
26. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.
【作业】如图①,直线 , 与的面积相等吗?为什么?
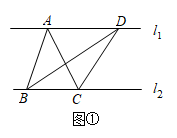
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .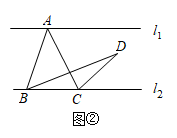
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .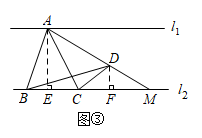
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .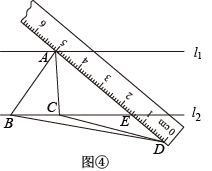 27. 根据以下素材,设计落地窗的遮阳篷.
27. 根据以下素材,设计落地窗的遮阳篷.素材1:如图1,小浩家的窗户朝南,窗户的高度 , 此地一年中的正午时刻,太阳光与地平面的最小夹角为 , 最大夹角为.如图2,小浩设计直角形遮阳篷 , 点C在的延长线上, , 它既能最大限度地使冬天温暖的阳光射入室内(太阳光与平行),又能最大限度地遮挡夏天炎热的阳光(太阳光与平行).
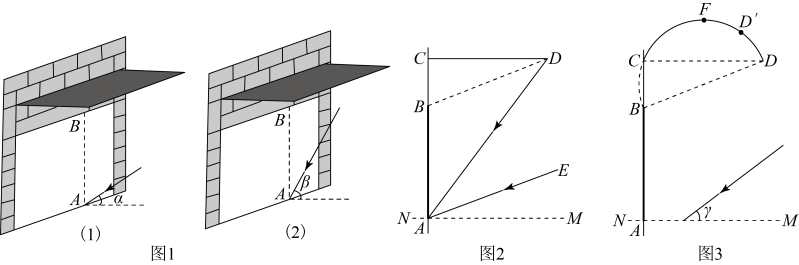
素材2:小浩查阅资料,计算出 , ( , , 如图2).
素材3:如图3,为了美观及实用性,小浩再设计出圆弧形可伸缩遮阳篷(劣弧延伸后经过点B,段可伸缩,F为的中点), , 的长保持不变.
(1)、【任务1】如图2,求 , 的长.(2)、【任务2】如图3,求劣弧的弓高.(3)、【任务3】如图3,若某时太阳光与地平面的夹角r的正切值 , 要最大限度地使阳光射入室内,求遮阳篷点D上升高度的最小值(点到的距离).
-