备考2024年浙江中考数学一轮复习专题17.2图形的初步 真题模拟集训
试卷更新日期：2024-03-02 类型：一轮复习
一、选择题（每题3分，共48分）
-
1. 如图所示，能用∠O，∠AOB，∠1三种方法表示同一个角的图形是（ ）A、
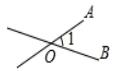B、
C、
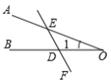D、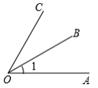
2. 将如图所示的长方体牛奶包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形可能是（ ）
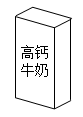A、
B、
C、
D、
3. 下列各图形中，经过折叠能围成一个立方体的为（ ）A、
B、
C、
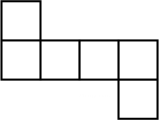D、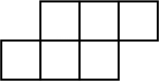
4. 在 的内部任取一点 ，作射线 ，那么有（ ）A、 B、 C、 D、5. 如图是脊柱侧弯的检测示意图，在体检时为方便测出Cobb角的大小，需将转化为与它相等的角，则图中与相等的角是（ ）
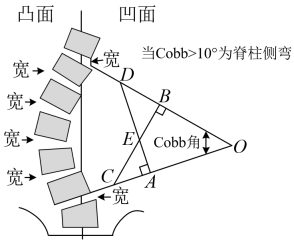A、 B、 C、 D、6. 小光准备从A地去往B地，打开导航、显示两地距离为37.7km，但导航提供的三条可选路线长却分别为45km，50km，51km（如图）.能解释这一现象的数学知识是（ ）
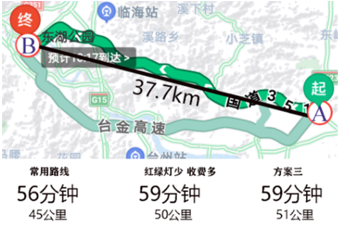A、两点之间，线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线7. 把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（ ）A、六边形 B、五边形 C、四边形 D、三角形8. 如图，直线相交于点O， ， 若 ， 则的度数为（ ）
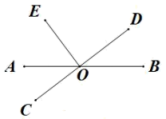A、 B、 C、 D、9. 如图1，点 ， ， 是数轴上从左到右排列的三个点，分别对应的数为-5，b，4，某同学将刻度尺如图2放置，使刻度尺上的数字0对齐数轴上的点A，发现点B对应刻度1.8cm，点C对齐刻度5.4cm．则数轴上点B所对应的数b为（ ）
A、3 B、-1 C、-2 D、-310. 如图，圆形挂钟分针针尖到圆心的距离为10cm，经过35分钟，分针针尖转过的弧长是（ ）
A、 πcm B、 πcm C、 πcm D、 πcm11. 小明从A处出发沿北偏东50°方向行走至B处，又从B处沿南偏东70°方向行走至C处，则∠ABC等于（ ）A、20° B、100° C、120° D、160°12. 如图是每个面都标注了字母的立方体表面展开图.在展开前，与标注字母 的面相对的面上的字母为（ ）
A、 B、 C、 D、13. 已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的.那么安放的位置是（ ）
A、① B、② C、③ D、④14. 如图，小聪用图1中的一副七巧板拼出如图2所示“鸟”，已知正方形ABCD的边长为4，则图2中E，F两点之间的距离为（ ）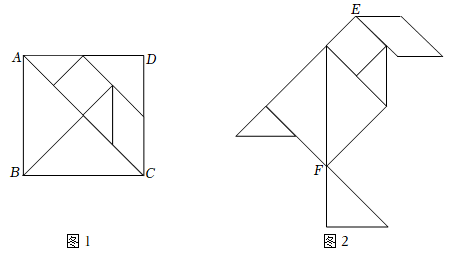
A、 B、2 C、 D、415. 七巧板是我国祖先的一项卓越创造，流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板，如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形，则这两个图形中，中国七巧板和日本七巧板能拼成的个数分别是（ ）
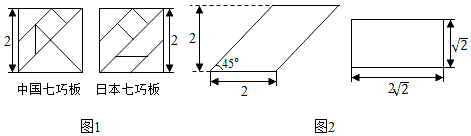A、1和1 B、1和2 C、2和1 D、2和216. 七巧板是我国祖先的一项卓越创造，下列四幅图是爱思考的小红同学用如图所示的七巧板拼成的，则这四个图形的周长从大到小排列正确（ )
A、乙>丙>甲>丁 B、乙>甲>丙>丁 C、两>乙>甲>丁 D、丙>乙>丁>甲二、填空题（每题4分，共28分）
-
17. 木工师傅用刨子可将木板刨平，如图，经过刨平的木板上的两个点，而且只能弹出一条墨线，其数学原理为.
18. 已知∠α和∠β互为补角，且∠β比∠α小30°，则∠β等于°19. 图1是一种矩形时钟，图2是时钟示意图，时钟数字2的刻度在矩形ABCD的对角线BD上，时钟中心在矩形ABCD对角线的交点O上.若 ，则BC长为cm（结果保留根号）.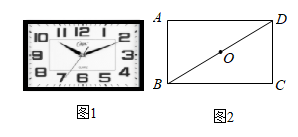
20. 将一个容积为360cm3的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．
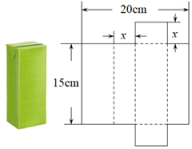21. 小明用图1中的一副七巧板拼出如图2所示的“火箭图”，若正方形ABCD的边长为4cm，则图2中M与N两点之间的距离为 cm．
22. 一个直棱柱的立体图如图所示，该几何体的表面积为cm2
23. 如图，一个立方体有盖盒子，棱长为8cm，当正方形PDCS合上时，点A与点P重合，点B与点S重合，此时，两个全等的长方形ADFE与长方形BCHG向内合上，且顶点E，G都落在AB边上，点E在点G的右侧， ．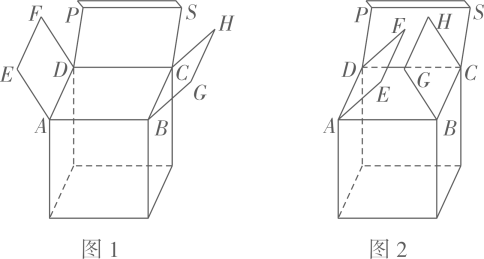
(1)、AE的长度是cm．(2)、长方形ADFE和长方形BCHG，从底面ABCD翻开的过程中，当且∠EAB最大时，∠EAB的余弦值为 ．三、作图题（共28分）
-
24. 将立方体纸盒沿某些棱剪开，且使六个面连在一起，然后铺平，可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是（填A或B）.
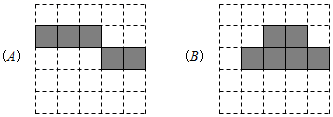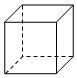
(2)、在以下方格图中，画一个与（1）中呈现的阴影部分不相似（包括不全等）的立方体表面展开图.（用阴影表示）
(3)、如图中的实线是立方体纸盒的剪裁线，请将其表面展开图画在右图的方格图中.（用阴影表示）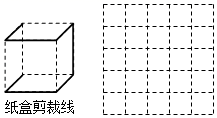
25. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）.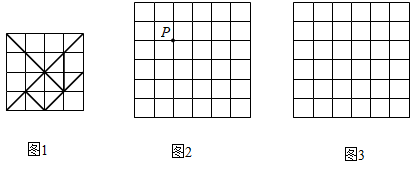
(1)、选一个四边形画在图2中，使点 为它的一个顶点，并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形，将它的各边长扩大到原来的 倍，画在图3中.四、实践探究题（共16分）
-
26. 综合与实践
主题：制作无盖正方体形纸盒
素材：一张正方形纸板．
步骤1：如图1，将正方形纸板的边长三等分，画出九个相同的小正方形，并剪去四个角上的小正方形；
步骤2：如图2，把剪好的纸板折成无盖正方体形纸盒．
猜想与证明：
(1)、直接写出纸板上与纸盒上的大小关系；(2)、证明（1）中你发现的结论．