广西崇左市钦州市名校2023-2024学年高一上学期期末教学质量监测数学试卷

试卷更新日期：2024-03-01 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，

1. 命题“存在一个五边形，它是轴对称图形”的否定是（）

A、存在无数个五边形，它是轴对称图形 B、存在一个五边形，它不是轴对称图形 C、任意一个五边形，它是轴对称图形 D、任意一个五边形，它不是轴对称图形

查看试题解析
2. 已知集合 $A = {x ∣ x^{2} - 2 x - 3 ⩽ 0} ， a = 1$ ，则（）

A、 $a \in A$ B、 $a \subseteq A$ C、 ${a} \in A$ D、 ${a} \cap A = A$

查看试题解析
3. 已知函数 $f (x) = {\begin{array}{l} - \frac{1}{x} ， x > 0 ， \\ x^{3} ， x ⩽ 0 ， \end{array}$ 则 $f (f (1)) =$ （）

A、0 B、1 C、2 D、-1

查看试题解析
4. 已知 $a = 2 ， b = l o g_{2} 5 ， c = 2^{\frac{1}{3}}$ ，则（）

A、 $b < c < a$ B、 $a < b < c$ C、 $c < a < b$ D、 $b < a < c$

查看试题解析
5. “ $3^{x} > 1$ ”是“ $\frac{1}{x} > 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 国家统计局发布的2018年至2022年我国城乡居民社会养老保险基金的收入和支出数据如图所示，则下列说法错误的是（）

A、2018年至2022年我国城乡居民社会养老保险基金收入逐年增加 B、2018年至2022年我国城乡居民社会产老保险基金支出逐年增加 C、2018年至2022年我国城乡居民社会养老保险基金收入数据的50%分位数为4852.9亿元 D、2018年至2022年我国城乡居民社会养老保险基金收入数据的40%分位数为4107.0亿元

查看试题解析
7. 已知 $a^{2} + b^{2} = a b + 4$ ，则 $a + b$ 的最大值为（）

A、2 B、4 C、8 D、 $2 \sqrt{2}$

查看试题解析
8. 把某种物体放在空气叫冷却，若该物体原来的温度是 ${θ_{1}}^{∘} C$ ，空气的温度是 ${θ_{0}}^{∘} C$ ，则 $t m i n$ 后该物体的温度 $θ^{∘} C$ 可由公式 $θ = θ_{0} + (θ_{1} - θ_{0}) e^{- \frac{t}{4}}$ 求得.若将温度分别为 $8 0^{∘} C$ 和 $6 0^{∘} C$ 的两块物体放入温度是 $2 0^{∘} C$ 的空气中冷却，要使得两块物体的温度之差不超过 $1 0^{∘} C$ ，则至少要经过（）（取： $l n 2 = 0.69$ ）

A、 $2.76 m i n$ B、4. $14 m i n$ C、 $5.52 m i n$ D、 $6.9 m i n$

查看试题解析

二、､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 已知 $a > 0$ ，且 $a \neq 1 ， a b = 1$ ，则函数 $y = a^{x}$ 与 $y = l o g_{x} x$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 已知 $a > b > c$ ，且 $a c < 0$ ，则（）

A、 $a^{2} > a c$ B、 $b c > c^{2}$ C、 $a^{2} > b^{2}$ D、 $\frac{1}{a} > \frac{1}{c}$

查看试题解析
11. 已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2}) (0 < x_{1} < x_{2})$ ，若幂函数 $f (x)$ 的图象经过点 $(9 ， 3)$ ，则（）

A、 $x_{1} + f (x_{1}) < x_{2} + f (x_{2})$ B、 $x_{1} - f (x_{1}) < x_{2} - f (x_{2})$ C、 $x_{1} f (x_{1}) < x_{2} f (x_{2})$ D、 $x_{2} f (x_{1}) < x_{1} f (x_{2})$

查看试题解析
12. 已知函数 $f (x) = a^{x^{2} + a} (a > 0$ 且 $a \neq 1)$ ，下列结论正确的是（）

A、 $f (x)$ 是偶函数 B、 $f (x)$ 的图象与直线 $y = 1$ 一定没有交点 C、若 $f (x)$ 的图象与直线 $y = a$ 有2个交点，则 $a$ 的取值范围是 $(0 ， 1)$ D、若 $f (x)$ 的图象与直线 $y = a$ 交于 $A ， B$ 两点，则线段 $A B$ 长度的取值范围是 $(0 ， 1)$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分，把答案填在答题卡中的横线上.

13. 函数 $y = \sqrt{x - 1} + 1$ 的定义域为.

查看试题解析
14. 某社区有60岁以上的居民800名，20岁至60岁的居民1800名，20岁以下的居民400名，该社区卫生室为了解该社区居民的身体健康状况，准备对该社区所有居民按年龄采用分层随机抽样的办法进行抽样调查，抽取了一个容量为150的样本，则样本中年龄在20岁以下的居民的人数为.

查看试题解析
15. 已知函数 $f (x) = l o g_{2} (a x^{2} + 2 x - 5 a)$ 在 $(2 ， + ∞)$ 上是增函数，则 $a$ 的取值范围是.

查看试题解析
16. 某单位举办演讲比赛，最终来自 $A ， B ， C ， D$ 四个部门共12人进入决赛，把 $A ， B ， C ， D$ 四个部门进入决赛的人数作为样本数据.已知样本方差为2.5，且样本数据互不相同，则样本数据中的最大值为.

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. 已知集合 $A = {- 1 ， 0 ， 1} ， B = {y ∣ y = 2^{x}}$ .

(1)、求 $A \cap B$ ；

(2)、求 $∁_{R} (A \cup B)$ .

查看试题解析
18. 已知函数 $f (x) = x + \frac{1}{x} (x > 0)$ ．

(1)、求 $f (x)$ 的最小值；

(2)、判断 $f (x)$ 在 $(1 ， + \infty)$ 上的单调性，并根据定义证明．

查看试题解析
19. 某果园为了更好地销售沃柑，需对其质量进行分析，以便做出合理的促销方案.现从果园内随机采摘200个沃柑进行称重，其质量（单位：克）分别在 $[95 ， 105) ， [105 ， 115) ， [115 ， 125) ， [125 ， 135) ， [135 ， 145) ， [145 ， 155]$ 中，其频率分布直方图如图所示.

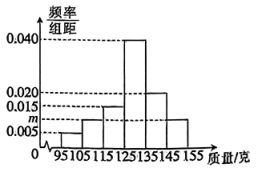(1)、求 $m$ 的值；

(2)、该果园准备将质量较大的 $20 %$ 的沃柑选为特级果，单独包装售卖，求被选为特级果的沃柑的质量至少为多少克.

查看试题解析
20. 已知函数 $f (x) = \frac{4}{2^{x} + 2}$ .

(1)、证明：若 $x_{1} + x_{2} = 2$ ，则 $f (x_{1}) + f (x_{2}) = 2$ .

(2)、求 $f (\frac{1}{3}) + f (\frac{2}{3}) + f (1) + f (\frac{4}{3}) + f (\frac{5}{3})$ 的值.

查看试题解析
21. 某果园占地约200公顷，拟种植某种果树，在相同种植条件下，该种果树每公顷最多可种植600棵，种植成本 $y$ （单位：万元）与果树数量 $x$ （单位：百棵）之间的关系如下表所示.
$x$
0
4
9
16
36
$y$
3
7
9
11
15
为了描述种植成本 $y$ 与果树数量 $x$ 之间的关系，现有以下三种模型供选择：① $y = b x + c$ ；② $y = b \sqrt{x} + c$ ；③ $y = b l o g_{a} x + c$ .

(1)、选出你认为最符合实际的函数模型，并写出相应的函数解析式.

(2)、已知该果园的年利润 $z$ （单位：万元）与 $x ， y$ 的关系式为 $z = 3 y - 0.1 x - 20$ ，则果树数量 $x$ 为多少时年利润最大？并求出年利润的最大值.

查看试题解析
22. 已知函数 $f (x) = 2 l o g_{a} (x + a) ， g (x) = l o g_{a} (3 x + a) ， a > 0$ 且 $a \neq 1$ .

(1)、若 $a = 3$ ，函数 $F (x) = f (x) - g (x)$ ，求 $F (x)$ 的定义域；

(2)、若 $\forall x \in (1 ， + ∞) ， f (x) > g (x)$ ，求 $a$ 的取值范围.

查看试题解析

$x$	0	4	9	16	36
$y$	3	7	9	11	15