广西桂林市2023-2024学年度高一上学期数学期末质量检测
试卷更新日期:2024-03-01 类型:期末考试
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 函数的定义域为( )A、 B、 C、 D、4. 不等式的解集为( )A、 B、 C、 D、5. 在同一坐标系中,函数y=( )x与y=log2x的图象大致是( )A、
 B、
B、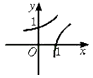 C、
C、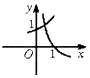 D、
D、 6. 三角形全等是三角形面积相等的( )A、充分但不必要条件 B、必要但不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知 , 则的大小关系为( )A、 B、 C、 D、8. 已知某物种年后的种群数量近似满足函数模型:( , 当时表示2023年初的种群数量).自2023年初起,经过年后 , 当该物种的种群数量不足2023年初的时,的最小值为(参考数据:)( )A、16 B、17 C、18 D、19
6. 三角形全等是三角形面积相等的( )A、充分但不必要条件 B、必要但不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知 , 则的大小关系为( )A、 B、 C、 D、8. 已知某物种年后的种群数量近似满足函数模型:( , 当时表示2023年初的种群数量).自2023年初起,经过年后 , 当该物种的种群数量不足2023年初的时,的最小值为(参考数据:)( )A、16 B、17 C、18 D、19二、多选题
-
9. 若 , 则( )A、 B、 C、 D、10. 已知函数 , 下列结论正确的是( )A、是奇函数 B、的图象不过原点 C、在区间上单调递增 D、在区间上单调递增11. 甲、乙两袋里有除颜色外完全相同的球.从甲袋中摸出一个红球的概率是 , 从乙袋中摸出一个红球的概率是 , 下列结论正确的是( )A、从甲袋中摸出一个球,不是红球的概率是 B、从乙袋中摸出一个球,不是红球的概率是 C、从两袋中各摸出一个球,2个球都是红球的概率为 D、从两袋中各摸出一个球,2个球都不是红球的概率为12. 下列区间上,函数有零点的是( )A、 B、 C、 D、
三、填空题
-
13. 某公司生产、、三种型号的新能源汽车,产量分别为1200辆、6000辆和2000辆.为检验该公司的产品质量,现用分层随机抽样的方法抽取46辆进行检验,则种型号的新能源车应抽取辆.14. 已知幂函数的图象经过点 , 则.15. 已知 , 则的最小值为.16. 一个样本容量为7的样本的平均数为5,方差为2.现样本加入新数据4,5,6,此时样本容量为10,方差为.
四、解答题
-
17. 已知集合 , .(1)、当时,求;(2)、若 , 求实数的取值范围.18. 2023年11月,首届全国学生(青年)运动会在广西举行.10月31日,学青会火炬传递在桂林举行,广西师范大学有5名教师参与了此次传递,其中男教师2名,女教师3名.现需要从这5名教师中任选2名教师去参加活动.(1)、写出试验“从这5名教师中任选2名教师”的样本空间;(2)、求选出的2名教师中至多有1名男教师的概率.19. 已知函数.(1)、判断在上的单调性,并用函数单调性的定义证明;(2)、求在上的值域.20. 在某校进行男生身高调查,随机抽取100名男生,测得他们的身高(单位:),并按照区间 , , , , 分组,得到如下的样本数据的频率分布直方图:
 (1)、估计该校一位男生的身高位于区间的概率及该校男生身高的分位数;(2)、估计该校男生的平均身高(同一组数据用该区间的中点值为代表).21. 疫情后全国各地纷纷布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力.某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:一工艺品在过去的一个月内(以30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表:
(1)、估计该校一位男生的身高位于区间的概率及该校男生身高的分位数;(2)、估计该校男生的平均身高(同一组数据用该区间的中点值为代表).21. 疫情后全国各地纷纷布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力.某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:一工艺品在过去的一个月内(以30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表:(天)
2
14
18
22
26
30
44
128
140
144
140
128
(1)、给出以下三个函数模型:①;②;③.请你根据上面的数据图表,从中选择最合适的一种函数模型来描述日销售量与时间的变化关系,并求出的解析式;(2)、已知第2天该工艺品的日销售收入为220元.求在过去的30天中,哪几天该工艺品的日销售收入不低于588元.22. 已知函数.(1)、当时,解不等式;(2)、若的最大值是 , 求的值;(3)、已知 , , 当的定义域为时,的值域为 , 求实数的取值范围.