广西壮族自治区三新学术联盟2023-2024学年高二上学期期末教学质量检测数学试题
试卷更新日期:2024-03-01 类型:期末考试
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 抛物线的焦点坐标是( )A、 B、 C、 D、2. 已知向量 , , 若 , 则z=( )A、﹣4 B、4 C、 D、3. 设P是椭圆上的动点,则P到该椭圆的两个焦点的距离之和为( )A、 B、 C、4 D、4. 已知等差数列的前5项之和为25, , 则公差为( )A、6 B、3 C、4 D、55. 已知两直线与的交点在圆的内部,则实数k的取值范围是( )A、 B、 C、 D、6. 正项等比数列的前n项和为 , , , 则等于( )A、9 B、72 C、70 D、487. 已知双曲线(),以双曲线C的右顶点A为圆心,b为半径作圆A , 圆A与双曲线C的一条渐近线交于M , N两点,若 , 则双曲线的离心率为( )A、 B、 C、 D、28. 如图所示空间直角坐标系A﹣xyz中,是正三棱柱的底面内一动点, , 直线PA和底面ABC所成的角为 , 则P点的坐标满足( )
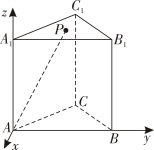 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 若圆M:与圆N:相交,则k的取值可能为( )A、 B、1 C、3.8 D、4.210. 关于x , y的方程表示的曲线可以是( )A、椭圆 B、双曲线 C、抛物线 D、圆11. 已知是等差数列,其前n项和为 , , 则下列结论一定正确的有( )A、 B、最小 C、 D、12. 如图,在长方体中,点P是底面内的动点,E , F , O , K分别为AB , BC , BD , 的中点,若 , 则下列说法正确的是( )
 A、的最大值为2 B、三棱锥P﹣ABD的体积不变,表面积改变 C、若平面 , 则 D、的最小值为
A、的最大值为2 B、三棱锥P﹣ABD的体积不变,表面积改变 C、若平面 , 则 D、的最小值为三、填空题:本题共4小题,每小题5分,共20分.
-
13. 若点在抛物线上,则该抛物线的方程为 .14. 已知空间向量 , , 则向量在向量上的投影向量的坐标是 .15. 如图所示是一系列有机物的结构简图,途中的“小黑点”表示原子,两黑点间的“短线”表示化学键,按图中结构第n个图的化学键和原子的个数之和为个.(用含n的代数式表示)
 16. 如图,棱长为1的正方体上有两个动点分别从顶点A , C同时出发,以相同的速度1分别向点B , D运动,最后同时到达,则在运动的过程中,两个动点间的最小距离为 .
16. 如图,棱长为1的正方体上有两个动点分别从顶点A , C同时出发,以相同的速度1分别向点B , D运动,最后同时到达,则在运动的过程中,两个动点间的最小距离为 .
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.
-
17. 在等比数列中,(1)、已知 , , 求前4项和;(2)、已知公比 , 前6项和 , 求 .18. 已知圆C经过 , 两点,且圆心C在直线上.(1)、求圆C的方程;(2)、过点的直线l与圆C交于P , Q两点,若 , 求直线l的方程.19. 已知的周长为 , 其中点 , .(1)、求点C的轨迹方程;(2)、设D为点A关于直线的对称点,求线段CD的长度的取值范围.20. 如图,O是圆柱下底面的圆心,该圆柱的轴截面是边长为4的正方形ABCD , P为线段AD上的动点,E , F为下底面上的两点,且 , , EF交AB于点G .
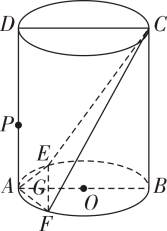 (1)、当时,证明:平面CEF;(2)、当为等边三角形时,求二面角的余弦值.
(1)、当时,证明:平面CEF;(2)、当为等边三角形时,求二面角的余弦值.