浙江省湖州市2023-2024学年高三上学期数学期末试卷

试卷更新日期：2024-03-01 类型：期末考试

进入出卷网下载

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $A = {x ∣ - 1 \leq x \leq 4} ， B = {x ∣ x < 3}$ ，则 $A \cup B =$ （）

A、 ${x ∣ - 1 \leq x < 3}$ B、 ${x ∣ - 1 \leq x \leq 4}$ C、 ${x ∣ x \leq 4}$ D、 ${x ∣ x < 3}$

查看试题解析
2. 已知复数 $z$ 满足 $(z - 1) i = 4 + 3 i$ （ $i$ 为虚数单位），则 $z + \bar{z} =$ （）

A、8 B、6 C、-6 D、-8

查看试题解析
3. 已知向量 $\vec{A B} = (\sqrt{3} ， 1) ， \vec{A C} = (2 \sqrt{3} ， - 2)$ ，则 $\vec{A B}$ 在 $\vec{A C}$ 上的投影向量是（）

A、 $(\frac{\sqrt{3}}{2} ， - \frac{1}{2})$ B、 $(\frac{\sqrt{3}}{2} ， \frac{1}{2})$ C、 $(- \frac{\sqrt{3}}{2} ， \frac{1}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， - \frac{1}{2})$

查看试题解析
4. 按从小到大顺序排列的两组数据：甲组： $27 ， 31 ， 37 ， m ， 42 ， 49$ ；乙组： $24 ， n ， 33 ， 44 ， 48 ， 52$ ，若这两组数据的第30百分位数､第50百分位数都分别对应相等，则 $m + n =$ （）

A、60 B、65 C、70 D、71

查看试题解析
5. 已知 $α \in (\frac{π}{2} ， π)$ ，且 $3 c o s 2 α - s i n α = 2$ ，则（）

A、 $c o s (π - α) = \frac{2}{3}$ B、 $t a n (π - α) = \frac{\sqrt{2}}{4}$ C、 $s i n (\frac{π}{2} - α) = \frac{\sqrt{5}}{3}$ D、 $c o s (\frac{π}{2} - α) = \frac{\sqrt{5}}{4}$

查看试题解析
6. 记 $S_{n}$ 是数列 ${a_{n}}$ 的前 $n$ 项和，设甲： ${a_{n}}$ 为等差数列；设乙： $S_{n} = \frac{n (a_{1} + a_{n})}{2}$ ，则（）

A、甲是乙的充分条件但不是必要条件 B、甲是乙的必要条件但不是充分条件 C、甲是乙的充要条件 D、甲既不是乙的充分条件也不是乙的必要条件

查看试题解析
7. 在正四棱锥 $P - A B C D$ 中，底面 $A B C D$ 的边长为 $2 ， △ P A C$ 为正三角形，点 $M ， N$ 分别在 $P B ， P D$ 上，且 $P M = 2 M B ， P N = 2 N D$ ，若过点 $A ， M ， N$ 的截面交 $P C$ 于点 $Q$ ，则四棱锥 $P - A M Q N$ 的体积是（）

A、 $\frac{2 \sqrt{6}}{3}$ B、 $\frac{4 \sqrt{6}}{3}$ C、 $\frac{2 \sqrt{6}}{9}$ D、 $\frac{4 \sqrt{6}}{9}$

查看试题解析
8. 已知函数 $f (x) = e^{x - 1} ， g (x) = a x^{2}$ ，若总存在两条不同的直线与函数 $y = f (x)$ ， $y = g (x)$ 图象均相切，则实数 $a$ 的取值范围是（）

A、 $(\frac{e}{4} ， + ∞)$ B、 $(\frac{e}{2} ， + ∞)$ C、 $(\frac{1}{e} ， + ∞)$ D、 $(\frac{2}{e} ， + ∞)$

查看试题解析

二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，至少有两个是符合题目要求的，全部选对的得5分，有选错的得0分，部分选对的得2分.

9. 下列结论中正确的是（）

A、在 $2 \times 2$ 列联表中，若每个数据 $a ， b ， c ， d$ 均变为原来的2倍，则 $χ^{2}$ 的值不变 $(χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)} ，其中 n = a + b + c + d)$ B、已知随机变量 $ξ$ 服从正态分布 $N (3 ， 4)$ ，若 $ξ = 2 η + 3$ ，则 $D (η) = 1$ C、在一组样本数据的散点图中，若所有样本点 $(x_{i} ， y_{i}) (i = 1 ， 2 ， \dots ， n)$ 都在直线 $y = 0.9 x + 1$ 上，则这组样本数据的样本相关系数为0.9 D、分别抛掷2枚相同的硬币，事件 $M$ 表示为“第1枚为正面”，事件 $N$ 表示为“两枚结果相同”，则事件 $M ， N$ 是相互独立事件

查看试题解析
10. 已知正数 $a ， b$ 满足 $a (a + b) = 1$ ，下列结论中正确的是（）

A、 $a^{2} + b^{2}$ 的最小值为 $2 \sqrt{2} - 2$ B、 $2 a + b$ 的最小值为2 C、 $\frac{1}{a} + \frac{1}{b}$ 的最小值为 $\frac{3 \sqrt{3}}{2}$ D、 $\sqrt{a} - \sqrt{b}$ 的最大值为1

查看试题解析
11. 纯音的数学模型是函数 $y = A s i n ω t$ ，但我们平时听到的乐音不止是一个音在响，而是许多个音的结合，称为复合音.复合音的产生是因为发声体在全段振动，产生频率为 $f$ 的基音的同时，其各部分，如二分之一､三分之一､四分之一部分也在振动，产生的频率恰好是全段振动频率的倍数，如 $2 f ， 3 f ， 4 f$ 等.这些音叫谐音，因为其振幅较小，我们一般不易单独听出来，所以我们听到的声音函数是 $y = s i n x + \frac{1}{2} s i n 2 x + \frac{1}{3} s i n 3 x + ⋯$ .记 $f_{n} (x) = s i n x + \frac{1}{2} s i n 2 x + \frac{1}{3} s i n 3 x + ⋯ + \frac{1}{n} s i n n x$ ，则下列结论中正确的是（）

A、 $x = π$ 为 $f_{2} (x)$ 的一条对称轴 B、 $f_{2} (x)$ 的周期为 $2 π$ C、 $f_{3} (x)$ 的最大值为 $\frac{2 \sqrt{2}}{3} + \frac{1}{2}$ D、 $f_{n} (x)$ 关于点 $(π ， 0)$ 中心对称

查看试题解析
12. 已知 $O$ 为坐标原点，点 $A (- 2 ， - 1)$ 在抛物线 $C ： x^{2} = - 2 p y$ 上，过点 $B (0 ， 1)$ 的直线交 $C$ 于 $P ， Q$ 两点，则下列结论中正确的是（）

A、 $C$ 的准线方程为 $y = 1$ B、直线 $A B$ 与 $C$ 相切 C、 $\vec{O P} \cdot \vec{O Q}$ 为定值3 D、 $| B P | \cdot | B Q | > | B A |^{2}$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分.

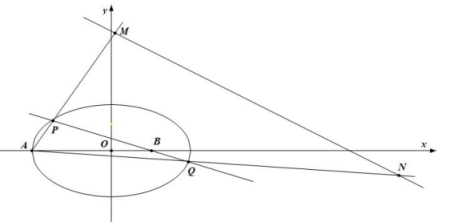
13. 已知 $(x - \frac{a}{x}) (1 - x)^{4}$ 的展开式中含 $x^{2}$ 项的系数为8，则实数 $a =$ .

查看试题解析
14. 已知圆 $C$ 的圆心在直线 $y = x + 1$ 上且与 $y$ 轴相切.请写出一个同时满足上述条件的圆的标准方程：.

查看试题解析
15. 已知一个圆台的上､下底面半径为 $a ， b (a < b)$ ，若球 $O$ 与该圆台的上､下底面及侧面均相切，且球 $O$ 与该圆台体积比为 $\frac{6}{13}$ ，则 $\frac{a}{b} =$ .

查看试题解析
16. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右顶点分别为 $A ， B$ ，点 $C$ 满足 $\vec{A C} = λ \vec{A B} (λ > 1)$ ，点 $P$ 为双曲线右支上任意一点（异于点 $B$ ），以 $A C$ 为直径的圆交直线 $A P$ 于点 $M$ ，直线 $B P$ 与直线 $C M$ 交于点 $N$ .若 $N$ 点的横坐标等于该圆的半径，则该双曲线的离心率是.

查看试题解析

四、解答题：本题共6小题，共70分，解答应写出必要的文字说明､证明过程及验算步骤.

17. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别是 $a ， b ， c$ ，已知 $a = \sqrt{3}$ ， $s i n B s i n C = \frac{3}{4} ， s i n A s i n (B - C) + s i n B s i n (C - A) = s i n C (s i n B - s i n C)$ .

(1)、求角 $A$ 的大小；

(2)、求 $△ A B C$ 的面积.

查看试题解析
18. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，数列 ${b_{n}}$ 为等差数列，且满足 $a_{1} = - 1 ， a_{2} + b_{3} = 0 ， S_{n} = 2 a_{n} + b_{n} (n \in N^{*})$ .

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、若数列 ${c_{n}}$ 满足 $c_{1} = b_{1}$ ，且 $c_{2 n} = c_{2 n - 1} + b_{1} ， c_{2 n + 1} = c_{2 n} + a_{n} (n \in N^{*})$ ，求数列 ${c_{n}}$ 的前 $2 n$ 项和 $T_{2 n}$ .

查看试题解析
19. 如图，在多面体 $A B C D E F$ 中，四边形 $A B C D$ 为平行四边形，且 $B D = \frac{1}{2} C D = 1 ， B D ⊥ C D . D E ⊥$ 平面 $A B C D$ ，且 $D E = \frac{1}{2} B F = \sqrt{3} ， D E$ $∥$ $B F$ .点 $H ， G$ 分别为线段 $D C ， E F$ 上的动点，满足 $D H = E G = λ (0 < λ < 2)$ .

(1)、证明：直线 $G H$ $∥$ 平面 $B C F$ ；

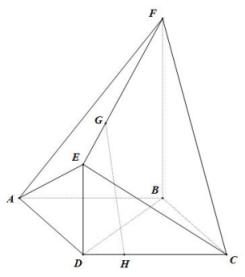(2)、是否存在 $λ$ ，使得直线 $G H$ 与平面 $A E F$ 所成角的正弦值为 $\frac{\sqrt{42}}{14}$ ？请说明理由.

查看试题解析
20. 杭州第19届亚运会，是继1990年北京亚运会､2010年广州亚运会之后，中国第三次举办亚洲最高规格的国际综合性体育赛事.2023年9月23日，杭州亚运会开幕式隆重举行.某电商平台亚运周边文创产品直播间，主播为当晚7点前登录该直播间的前 $N$ 名观众设置了两轮“庆亚运､送吉祥物”的抽奖活动.每轮抽奖都是由系统独立､随机地从这 $N$ 名观众中抽取15名幸运观众，抽中者平台会有亚运吉祥物玩偶赠送.而直播时这 $N$ 名观众始终在线，记两次抽奖中被抽中的幸运观众总人数为 $X$ （幸运观众总人数不重复计数，例如若某幸运观众两次都被抽中，但只记为1人）.

(1)、已知小杭是这前 $N$ 名观众中的一人，若小杭被抽中的概率为 $\frac{5}{9}$ ，求 $N$ 的值；

(2)、当 $P (X = 20)$ 取到最大值时，求 $N$ 的值.

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $A (- 3 ， 0)$ ，且离心率为 $\frac{\sqrt{6}}{3}$ .过点 $B (\frac{3}{2} ， 0)$ 的直线交 $C$ 于 $P ， Q$ 两点（异于点 $A$ ）.直线 $A P ， A Q$ 分别交直线 $x + 2 y - 9 = 0$ 于 $M ， N$ 两点.

(1)、求证：直线 $A P$ 与直线 $A Q$ 的斜率之积为定值；

(2)、求 $△ A M N$ 面积的最小值.

查看试题解析
22. 已知函数 $f (x) = l n a x + (a x - a - 1) e^{x - 1} - a x (a > 0)$ .

(1)、是否存在实数 $a$ ，使得函数 $f (x)$ 在定义域内单调递增；

(2)、若函数 $f (x)$ 存在极大值 $M$ ，极小值 $N$ ，证明： $M + N < - 4$ .（其中 $e \approx 2.71828$ 是自然对数的底数）

查看试题解析