广东省广州市天河区2023-2024学年高一(上)期末数学试卷
试卷更新日期:2024-03-01 类型:期末考试
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. =( )A、 B、 C、 D、2. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 已知克糖水中含有克糖 , 再添加克糖假设全部溶解 , 糖水变甜了将这一事实表示成一个不等式为( )A、 B、 C、 D、4. 已知点在角的终边上,则的值为( )A、 B、 C、 D、5. 如图中,中不属于函数 , , 中一个的是( )
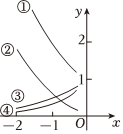 A、 B、 C、 D、6. 已知 , 若 , 则实数为( )A、或 B、或 C、或 D、7. 已知 , , , 则 , , 的大小关系正确的是( )A、 B、 C、 D、8. 定义在上的函数满足:是奇函数,且函数的图象与函数的交点为 , , , 则( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知 , 若 , 则实数为( )A、或 B、或 C、或 D、7. 已知 , , , 则 , , 的大小关系正确的是( )A、 B、 C、 D、8. 定义在上的函数满足:是奇函数,且函数的图象与函数的交点为 , , , 则( )A、 B、 C、 D、二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
-
9. 已知集合 , 则( )A、 B、 C、 D、10. 下列说法正确的是( )A、与的终边相同 B、若 , 则 C、若是第二象限角,则是第一象限角 D、已知某扇形的半径为 , 面积为 , 那么此扇形的弧长为11. 教材中用二分法求方程的近似解时,设函数来研究,通过计算列出了它的对应值表:
h分析表中数据,则下列说法正确的是( )
A、 B、方程有实数解 C、若精确度到 , 则近似解可取为 D、若精确度为 , 则近似解可取为12. 已知函数 , (m∈R,e为自然对数的底数),则( )A、函数至少有个零点 B、函数至多有个零点 C、当时,若 , 则 D、当时,方程恰有个不同实数根三、填空题:本题共4小题,每小题5分,共20分。
-
13. 命题“ , “的否定是 .14. 已知函数在上单调递增,若 , 则实数的取值范围为 .15. 已知指数函数和幂函数的图象都过点 , 若 , 则 .16. 立德学校为了表彰在体育运动会上表现优秀的班级,特制作了一批奖杯,奖杯的剖面图形如图所示,其中扇形的半径为 , , , , 则 用表示 , 据调研发现,当最长时,该奖杯比较美观,此时的值为 .

四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
17. 本小题分
已知集合 , , 全集 .
(1)、求;(2)、若 , 求实数的取值范围.18. 已知函数 .(1)、判断的奇偶性,并根据定义证明;(2)、判断函数在区间上单调性,并根据定义证明.19. 已知角是第二象限角,它的终边与单位圆交于点 .(1)、若 , 求的值;(2)、若 , 求的值.20. 某呼吸机生产企业本年度计划投资固定成本万元引进先进设备,用于生产救治新冠患者的无创呼吸机,每生产单位:百台另需投入成本万元 , 当年产量不足百台时,万元;当年产量不小于百台时,万元 , 据以往市场价格,每百台呼吸机的售价为万元,且依据疫情情况,预测该年度生产的无创呼吸机能全部售完.(1)、求年利润万元关于年产量百台的函数解析式;利润销售额一投入成本固定成本(2)、当年产量为多少时,年利润最大?并求出最大年利润.