广东省揭阳市2023-2024学年高一上学期期末教学质量监测数学试卷(含解析).doc
试卷更新日期:2024-03-01 类型:期末考试
一、单项选择题(本题共8道小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知条件 , 条件 , 则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 已知幂函数在区间上单调递减,则( )A、-1 B、3 C、1或-3 D、-1或34. 函数的零点一定位于下列哪个区间( )A、 B、 C、 D、5. 若 ,则 ( )A、 B、 C、 D、6. 已知是自然对数的底数,设 , 则的大小关系是( )A、 B、 C、 D、7. 鹅被人类称为美善天使,它不仅象征着忠诚、长久的爱情,同时它的生命力很顽强,因此也是坚强的代表.除此之外,天鹅还是高空飞翔冠军,飞行高度可达9千米,能飞越世界最高山峰“珠穆朗玛峰”.如图是两只天鹅面对面比心的图片,其中间部分可抽象为如图所示的轴对称的心型曲线.下列选项中,两个函数的图象拼接在一起后可大致表达出这条曲线的是( )
 A、及 B、及 C、及 D、及8. 已知函数 , 先将的图象上所有点的横坐标缩短到原来的(纵坐标不变),再将得到的图象上所有的点向右平移个单位长度,得到的图象关于轴对称,则的最小值为( )A、 B、 C、 D、
A、及 B、及 C、及 D、及8. 已知函数 , 先将的图象上所有点的横坐标缩短到原来的(纵坐标不变),再将得到的图象上所有的点向右平移个单位长度,得到的图象关于轴对称,则的最小值为( )A、 B、 C、 D、二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
-
9. 已知函数的定义域为 , 其图象如图所示,则下列说法中正确的( )
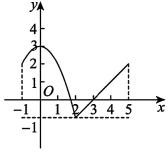 A、的单调递减区间为 B、的最大值为2 C、的最小值为-1 D、的单调递增区间为和10. 已知不等式的解集为 , 则下列结论正确的是( )A、 B、 C、 D、11. 下列说法正确的是( )A、如果 是第一象限的角,则 是第四象限的角 B、如果 是第一象限的角,且 则 C、若圆心角为 的扇形的弧长为 ,则该扇形面积为 D、若圆心角为 的扇形的弦长为 ,则该扇形弧长为12. 下列结论正确的有( )A、函数的最小值为2 B、函数且的图像恒过定点 C、的定义域为 , 则 D、的值域为 , 则
A、的单调递减区间为 B、的最大值为2 C、的最小值为-1 D、的单调递增区间为和10. 已知不等式的解集为 , 则下列结论正确的是( )A、 B、 C、 D、11. 下列说法正确的是( )A、如果 是第一象限的角,则 是第四象限的角 B、如果 是第一象限的角,且 则 C、若圆心角为 的扇形的弧长为 ,则该扇形面积为 D、若圆心角为 的扇形的弦长为 ,则该扇形弧长为12. 下列结论正确的有( )A、函数的最小值为2 B、函数且的图像恒过定点 C、的定义域为 , 则 D、的值域为 , 则三、填空题(本题共4小题,每小题5分,共20分)
-
13. 已知 , 则.14. 已知命题 , 若命题是假命题,则实数的取值范围是.15. 函数是定义在上的偶函数,并且当时, , 那么.16. 已知函数.若有2个零点,则实数的取值范围是.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
17.(1)、求值:;(2)、已知 , 求的值.18. 如图,在平面直角坐标系中,锐角和钝角的终边分别与单位圆交于两点.点的横坐标是 , 点的纵坐标是.
 (1)、求的值;(2)、求的值.19. 已知函数且的图象过点.(1)、求的值及的定义域;(2)、判断的奇偶性,并说明理由.20. 已知函数 .(1)、求 的最小正周期,并求 的最小值及取得最小值时 的集合;(2)、令 ,若 对于 恒成立,求实数 的取值范围.21. 研究表明,过量的碳排放会导致全球气候变暖等问题,因而减少碳排放具有深远的意义.为了响应国家节能减排的号召,2023年某企业计划引进新能源汽车生产设备.通过市场分析,全年投入固定成本2500万元,每生产(单位:百辆)新能源汽车需另投入成本(单位:万元),且 , 如果每辆车的售价为5万元,且假设全年内生产的车辆当年能全部销售完.(注:利润销售额-成本)(1)、求2023年的利润(万元)关于年产量(百辆)的函数关系式;(2)、当2023年的年产量为多少百辆时,企业所获利润最大?并求出最大利润.22. 已知定义域为的函数是奇函数.(1)、求实数的值.(2)、试判断的单调性,并用定义证明.(3)、解关于的不等式.
(1)、求的值;(2)、求的值.19. 已知函数且的图象过点.(1)、求的值及的定义域;(2)、判断的奇偶性,并说明理由.20. 已知函数 .(1)、求 的最小正周期,并求 的最小值及取得最小值时 的集合;(2)、令 ,若 对于 恒成立,求实数 的取值范围.21. 研究表明,过量的碳排放会导致全球气候变暖等问题,因而减少碳排放具有深远的意义.为了响应国家节能减排的号召,2023年某企业计划引进新能源汽车生产设备.通过市场分析,全年投入固定成本2500万元,每生产(单位:百辆)新能源汽车需另投入成本(单位:万元),且 , 如果每辆车的售价为5万元,且假设全年内生产的车辆当年能全部销售完.(注:利润销售额-成本)(1)、求2023年的利润(万元)关于年产量(百辆)的函数关系式;(2)、当2023年的年产量为多少百辆时,企业所获利润最大?并求出最大利润.22. 已知定义域为的函数是奇函数.(1)、求实数的值.(2)、试判断的单调性,并用定义证明.(3)、解关于的不等式.