广西百色市平果市2023-2024学年高二下学期数学开学考试试卷

试卷更新日期：2024-03-01 类型：开学考试

进入出卷网下载

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 在数列 ${a_{n}}$ 中，已知 $a_{n + 1} = a_{n} + \frac{1}{a_{n}}$ ，且 $a_{1} = 1$ ，则 $a_{4}$ 等于（）

A、2 B、 $\frac{5}{2}$ C、 $\frac{29}{10}$ D、29

查看试题解析
2. 已知两个向量 $\vec{a} = (1 ， 1 ， 2) ， \vec{b} = (1 ， 1 ， m)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则m的值为（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
3. 若方程 $\frac{x^{2}}{2 + m} - \frac{y^{2}}{2 - m} = 1$ 表示双曲线，则 $m$ 的取值范围是（）

A、 $- 2 < m < 2$ B、 $m > - 2$ C、 $m \geq 0$ D、 $m > 2$

查看试题解析
4. 已知等比数列 $\{a_{n}\}$ 的前 $n$ 项和为 $S_{n}$ ，且满足 $\frac{S_{8}}{S_{4}} = 17$ ，则公比 $q$ =（）

A、 $\frac{1}{2}$ B、 $\pm \frac{1}{2}$ C、2 D、 $\pm 2$

查看试题解析
5. 下列关于双曲线 $Γ$ ： $\frac{x^{2}}{6} - \frac{y^{2}}{3} = 1$ 的判断，正确的是（）

A、渐近线方程为 $x \pm 2 y = 0$ B、焦点坐标为 $(\pm 3 ， 0)$ C、实轴长为12 D、顶点坐标为 $(\pm 6 ， 0)$

查看试题解析
6. 已知 $⊙ O ： x^{2} + y^{2} = r^{2}$ ，直线 $l ： 2 x + 3 y = r^{2}$ ，若l与⊙O相离，则（）

A、点 $P (2 ， 3)$ 在l上 B、点 $P (2 ， 3)$ 在 $⊙ O$ 上 C、点 $P (2 ， 3)$ 在 $⊙ O$ 内 D、点 $P (2 ， 3)$ 在 $⊙ O$ 外

查看试题解析
7. 已知直线 $l_{1} ： (k - 3) x + (3 - k) y + 1 = 0$ 与 $l_{2} ： 2 (k - 3) x - 2 y + 3 = 0$ 垂直，则 $k$ 的值是（）

A、 $2$ 或 $3$ B、 $3$ C、 $2$ D、 $2$ 或 $- 3$

查看试题解析
8. 已知F为抛物线C：x²=8y的焦点，P为抛物线C上一点，点M的坐标为 $(- 4 ， 3)$ ，则 $△ P M F$ 周长的最小值是（）

A、 $5 + \sqrt{15}$ B、 $5 + \sqrt{17}$ C、9 D、 $5 + 3 \sqrt{2}$

查看试题解析

二、多选题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。

9. 设 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，且 $S_{n} = n + \frac{1}{2^{n}} - 1$ ，若数列 ${b_{n}}$ 满足： $b_{n} = n (1 - a_{n})$ ，且 $T_{n} = b_{1} + b_{2} + \dots + b_{n}$ ，则以下说法正确的是（）

A、数列 ${a_{n} - 1}$ 是等比数列 B、数列 ${b_{n}}$ 是递增数列 C、 $T_{n} = 2 - \frac{n + 2}{2^{n}}$ D、 $S_{n} ⩾ T_{n}$

查看试题解析
10. 已知在空间直角坐标系中，O为坐标原点，且 $A (1 ， 0 ， 2) ， B (- 1 ， 1 ， 1) ， C (3 ， 1 ， 2)$ ，则下列结论正确的是（）

A、 $| \vec{A B} | = 3$ B、 $(\vec{A B} + \vec{A C}) \cdot \vec{B C} = - 1$ C、 $\vec{A B} ⊥ \vec{A C}$ D、若 $\vec{O P} = \frac{1}{2} \vec{O A} + \frac{1}{3} \vec{O B} + \frac{1}{6} \vec{O C}$ ，则P ， A ， B ， C四点共面

查看试题解析
11. 如图，棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 为线段 $A_{1} B$ 上的动点（不含端点），则下列结论正确的是（）

A、直线 $D_{1} P$ 与 $A C$ 所成的角可能是 $\frac{π}{6}$ B、平面 $D_{1} A_{1} P ⊥$ 平面 $A_{1} A P$ C、三棱锥 $D_{1} - C D P$ 的体积为定值 D、平面 $A P D_{1}$ 截正方体所得的截面可能是等腰梯形

查看试题解析
12. 伟大的古希腊哲学家、百科式科学家阿基米德最早采用不断分割法求得椭圆的面积为椭圆的长半轴长和短半轴长乘积的 $π$ 倍，这种方法已具有积分计算的雏形．已知椭圆C的面积为 $6 π$ ，离心率为 $\frac{\sqrt{5}}{3}$ ， $F_{1} ， F_{2}$ 是椭圆C的两个焦点，P为椭圆C上的动点，则下列选项正确的有（）

A、椭圆C的标准方程可以为 $\frac{y^{2}}{9} + \frac{x^{2}}{4} = 1$ B、 $△ F_{1} P F_{2}$ 的周长为10 C、 $| P F_{1} | \cdot | P F_{2} | \leq 9$ D、 $c o s ∠ F_{1} P F_{2} \geq - \frac{1}{9}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分

13. 已知数列 ${a_{n}}$ 是等比数列，且 $a_{n} > 0$ ， $a_{3} a_{5} + 2 a_{4} a_{6} + a_{5} a_{7} = 25$ ，则 $a_{4} + a_{6} =$ ．

查看试题解析
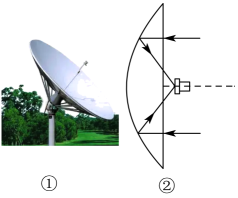
14. 已知直线 $l_{1} ： 4 x + 3 y - 1 = 0$ 与直线 $l_{2} ： 8 x + 6 y - 6 = 0$ ，则 $l_{1}$ 与 $l_{2}$ 之间的距离为.

查看试题解析
15. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ，点A在双曲线C上， $A F_{2} ⊥ F_{1} F_{2}$ ，直线 $A F_{1}$ 与双曲线C交于另一点B ， $\vec{F_{1} A} = 4 \vec{F_{1} B}$ ，则双曲线C的离心率为.

查看试题解析
16. 某学习小组研究一种卫星接收天线（如图①所示），发现其曲面与轴截面的交线为抛物线，在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线，经反射聚焦到焦点处（如图②所示）．已知接收天线的口径（直径）为 $2.4$ ，深度为 $0.4$ ，则该抛物线的焦点到顶点的距离为．

查看试题解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17. 已知圆 $C ： x^{2} + y^{2} - 4 x - 5 = 0$ ．

(1)、求直线 $y = 2 x$ 被圆截得弦长；

(2)、已知 $A (0 ， \sqrt{5})$ 为圆C上一点，求与圆C外切于点A ，且半径为6的圆 $M$ 的方程．

查看试题解析
18. 已知等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{5} - a_{1} = S_{4} = 30$ .

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ ；

(2)、若 ▲ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ .
在① $b_{n} = l o g_{2} a_{n + 1} + a_{n}$ ， ② $b_{n} = \frac{1}{(l o g_{2} a_{n} + 1) \cdot (l o g_{2} a_{n + 1} + 1)}$ ， ③ $b_{n} = n \cdot a_{n}$
这三个条件中任选一个补充在第（2）问中，并求解.注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
19. 已知曲线C是到两个定点 $A (- 2 ， 0)$ ， $B (2 ， 0)$ 的距离之比等于常数 $\sqrt{5}$ 的点组成的集合．

(1)、求曲线C的方程；

(2)、设过点B的直线l与C交于M，N两点；问在x轴上是否存在定点 $Q (t ， 0)$ ，使得 $\vec{Q M} \cdot \vec{Q N}$ 为定值？若存在，求出点Q的坐标及定值；若不存在，请说明理由．

查看试题解析
20. 四棱锥 $P - A B C D$ 底面为平行四边形，且 $∠ A B C = 6 0^{∘}$ ， $A B = 2$ ， $A D = 3$ ， $P A ⊥$ 平面 $A B C D$ ， $B M = \frac{1}{3} B C$ ．

(1)、点 $N$ 在棱 $P D$ 上，且 $\frac{P N}{N D} = \frac{1}{3}$ ，求证： $P B$ $∥$ 平面 $A M N$ ；

(2)、若异面直线 $A B$ 与 $P D$ 所成角的余弦值为 $\frac{\sqrt{3}}{4}$ ，求平面 $P A M$ 与平面 $P C D$ 所成锐二面角的余弦值．

查看试题解析
21. 已知数列 ${a_{n}}$ 的前n项和 $S_{n}$ ，且 $S_{n} = 2 a_{n} - 2 n - 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、令 $b_{n} = \frac{2 n + 1}{a_{n} + 2}$ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ .

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个焦点为 $F (1 ， 0)$ ，且离心率为 $\frac{1}{2}$ .

(1)、求 $C$ 的方程；

(2)、过 $F$ 作直线 $l$ 与 $C$ 交于 $M ， N$ 两点， $O$ 为坐标原点，若 $S_{△ O M N} = \frac{6 \sqrt{2}}{7}$ ，求 $l$ 的方程.

查看试题解析