广东省汕头市濠江区2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-01 类型：期末考试

进入出卷网下载

一、选择题（本大题10题，每小题3分，共30分．在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑）

1. $- 3$ 的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是（）

A、13×10⁵ B、1.3×10⁵ C、1.3×10⁶ D、1.3×10⁷

查看试题解析
3. 单项式-3mn²的系数是（）

A、9 B、-3 C、3 D、-9

查看试题解析
4. 如图所示的三棱柱的展开图不可能是（）

A、 B、 C、 D、

查看试题解析
5. 有理数 $a$ ， $b$ 在数轴上的位置如图所示，则下列说法正确的是（）

A、 $a + b < 0$ B、 $a - b > 0$ C、 $a b < 0$ D、 $| a | > | b |$

查看试题解析
6. 如图，钟表8时30分时，时针与分针所成的角的度数为（）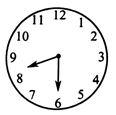

A、30° B、60° C、75° D、90°

查看试题解析
7. 若关于 $x$ 的方程 $a x + 3 x = 2$ 的解是 $x = 1$ ，则 $a$ 的值是（）

A、1 B、5 C、-1 D、-5

查看试题解析
8. 若 $3 a = 5 b$ ，则下列等式中一定成立的是（）

A、 $\frac{a}{3} = \frac{b}{5}$ B、 $3 a + 5 b = 0$ C、 $3 a - 3 b = 2 b$ D、 $3 (a + 1) = 5 (b + 1)$

查看试题解析
9. 中国古代问题：有甲、乙两个牧童，甲对乙说：“把你的羊给我一只，我的羊数就是你的羊数的2倍”.乙回答说：“最好还是把你的羊给我一只，我们羊数就一样了”.若设甲有x只羊，则下列方程正确的是（）

A、x+1=2（x﹣2） B、x+3=2（x﹣1） C、x+1=2（x﹣3） D、 $x - 1 = \frac{x + 1}{2} + 1$

查看试题解析
10. 已知 $x$ 满足 $| x - 4 | = 4 - x$ ，则 $x$ 不可能是（）

A、 $- 1$ B、0 C、5 D、4

查看试题解析

二、填空题（本大题6题，每小题3分，共18分．请将下列各题的正确答案填写在答题卡相应的位置上）

11. 一个角的度数是 $45 °$ ，则它的余角的度数为．

查看试题解析
12. 已知 $| x - 2 | + | y + 3 | = 0$ ，则 $x + y =$ ．

查看试题解析
13. 如图所示的网格是正方形网格， $∠ A B C$ $∠ D E F$ ．（填“ $>$ ”“ $=$ ”或“ $<$ ”）

查看试题解析
14. 点A在数轴上表示的数为 $a$ 、点 $B$ 先向右移动3个单位，又向左移动6个单位到达点A ，则点 $B$ 在数轴上表示的数为．

查看试题解析
15. 当 $x = 1$ 时， $k x + b$ 的值为6，则 $3 - k - b$ 的值是．

查看试题解析
16. 按下面的程序计算：若输入正整数x的值，输出结果是133，则满足条件的x的值是．

查看试题解析

三、解答题（本大题共9小题，满分72分．第17、18题各4分，第19、20题各6分，第21题8分，第22、23题各10分，第24、25题各12分．解答应写出文字说明、证明过程或演算步骤．）

17. 计算： ${(- 1)}^{10} \times 2 + {(- 2)}^{3} \div 4$ ．

查看试题解析
18. 解方程：8x＝﹣2（x+4）．

查看试题解析
19. 如图所示，在无阴影的方格中选出两个画出阴影，使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图．（填出两种答案）

查看试题解析
20. 从某一批次的袋装食品中抽取20袋，若每袋食品以500克为标准质量，分别用正、负数表示超过或不足的部分，记录如下：
与标准质量的差值（单位：克）
$- 20$
$- 5$
0
2
3
10
袋数
4
1
3
4
5
3

(1)、这20袋食品中质量最大的比质量最小的重多少克？

(2)、求这20袋食品一共有多少克？

查看试题解析
21. 【概念探究】在学习了有理数的乘方运算后．小芳对类似于 $(- 5) \div (- 5) \div (- 5) \div (- 5)$ 这样几个相同有理数（均不等于0）的除法运算产生了兴趣，决定探究学习．经过查阅资料，类比有理数的乘方运算，小芳知道这种除法运算叫做除方，并把 $(- 5) \div (- 5) \div (- 5) \div (- 5)$ 记作 ${(- 5)}_{4}$ ，读作“ $- 5$ 的4次商”．
【概念归纳】一般地，我们把 $n$ 个 $a$ （ $a \neq 0$ ）相除记作 $a_{n}$ ，读作“ $a$ 的 $n$ 次商”

(1)、【概念理解】直接写出结果： ${(- 1)}_{3} =$ ．

(2)、关于除方，下列说法正确的是：（填序号）
①任何非零数的2次商都等于1；②对于任何正整数 $n$ ， ${(- 1)}_{n} = - 1$ ；③ $3_{4} = 4_{3}$ ；
④负数的奇数次商结果是负数，负数的偶数次商结果是正数

(3)、【概念运用】经过探究，小芳发现有理数的除方运算可转化为乘方运算，例： $3_{4} = 3 \div 3 \div 3 \div 3$ $= 3 \times \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3} = {(\frac{1}{3})}^{2}$ ．仿照上面的算式，将下列运算结果直接写成乘方（幂）的形式：
${(- 5)}_{4} =$ ； ${(\frac{1}{3})}_{n} =$ ．

(4)、计算： $5_{2} \div {(- \frac{1}{3})}_{5} \times {(- \frac{1}{2})}_{3} + {(- \frac{1}{7})}_{3} \times \frac{1}{7}$ ．

查看试题解析
22. 如图，这是某新建的交通环岛的简化模型（因路段 $F G$ 还未完成施工，禁止车辆从 $F G$ 驶进或驶出环岛），试通车前环岛上没有车辆，试通车期间该交通环岛的进出机动车辆数如图所示，已知试通车期间从路口 $D E$ 驶入了 $x_{3}$ 辆机动车，图中箭头方向表示车辆的行驶方向，图中 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 分别表示该时段单位时间内通过路段 $A B$ ， $C D$ ， $E H$ 的所有机动车辆数．

(1)、若 $x_{3} = 10$ ，则
① $x_{1} =$ _▲_， $x_{2} =$ _▲_．（用含a ， b的代数式表示 $x_{1}$ ， $x_{2}$ ）
②当 $a = 6$ ， $b = 4$ 时，判断 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小．

(2)、若该时段内，通过路段 $A B$ ， $E H$ 的车辆数相同，且通过路段 $C D$ 的车辆比路段 $E H$ 的车辆少 $15$ 辆，分别求 $a$ ， $b$ 的值．

查看试题解析
23. 已知 $∠ A O B = 120 °$ ， $∠ C O D$ 在 $∠ A O B$ 内部．

图1 图2 图3

(1)、如图1，若 $∠ B O D = 30 °$ ， $∠ C O D = 60 °$ ，求 $∠ A O C$ 的度数；

(2)、如图2，在（1）的情况下，若 $O E$ 平分 $∠ B O C$ ，请说明： $∠ A O C = 2 ∠ D O E$ ；

(3)、如图3，若在 $∠ A O B$ 的外部分别作 $∠ A O C$ ， $∠ B O D$ 的余角 $∠ A O P$ ， $∠ B O Q$ ，试探究 $∠ A O P$ ， $∠ B O Q$ ， $∠ C O D$ 三者之间的数量关系，并说明理由．

查看试题解析
24. 如图，数轴上点 $A$ 表示的数为 $- 4$ ，点 $B$ 表示的数为16，点 $P$ 从点 $A$ 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点 $Q$ 从点 $B$ 出发，以每秒2个单位长度的速度向左匀速运动，设运动时间为 $t$ 秒（ $t > 0$ ）

(1)、A ， $B$ 两点间的距离等于，线段 $A B$ 的中点表示的数为；

(2)、求当 $t$ 为何值时， $P Q = \frac{1}{2} A B$ ？

(3)、若点 $M$ 为 $P Q$ 的中点，当点 $M$ 到原点距离为9时，求 $t$ 的值．

查看试题解析

与标准质量的差值（单位：克）	$- 20$	$- 5$	0	2	3	10
袋数	4	1	3	4	5	3