新疆乌鲁木齐市重点中学2023-2024学年九年级上学期数学月考考试试卷(12月)
试卷更新日期:2024-03-01 类型:月考试卷
一、选择题(本大题共9小题,每小题4分,共36分)每题所给的四个选项中只有一项是符合题目要求的,请将选项的代号字母填在答卷的相应位置处.
-
1. 下列图标中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知的半径是 , , 则点P在( )A、的内部 B、外部 C、上 D、不能确定3. 将抛物线 向左平移 个单位长度,再向下平移 个单位长度后,就得到抛物线( )A、 B、 C、 D、4. 如图, 是 的直径, 是弦,若 ,则 等于( )
2. 已知的半径是 , , 则点P在( )A、的内部 B、外部 C、上 D、不能确定3. 将抛物线 向左平移 个单位长度,再向下平移 个单位长度后,就得到抛物线( )A、 B、 C、 D、4. 如图, 是 的直径, 是弦,若 ,则 等于( )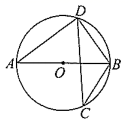 A、68° B、64° C、58° D、32°5. 已知a , b是方程的两个实数根,则的值为( )A、6 B、4 C、10 D、06. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )
A、68° B、64° C、58° D、32°5. 已知a , b是方程的两个实数根,则的值为( )A、6 B、4 C、10 D、06. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )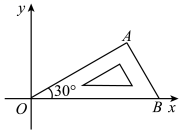 A、 B、 C、 D、7. 已知二次函数 , 下列关于其图象的结论中,错误的是( )A、开口向上 B、关于直线对称 C、当时,y随x的增大而增大 D、与x轴有交点8. 如图,过点作的切线 , , 切点分别是 , , 连接 . 过上一点作的切线,交 , 于点 , . 若 , 的周长为4,则的长为( )
A、 B、 C、 D、7. 已知二次函数 , 下列关于其图象的结论中,错误的是( )A、开口向上 B、关于直线对称 C、当时,y随x的增大而增大 D、与x轴有交点8. 如图,过点作的切线 , , 切点分别是 , , 连接 . 过上一点作的切线,交 , 于点 , . 若 , 的周长为4,则的长为( )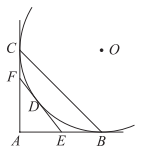 A、2 B、 C、4 D、9. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
A、2 B、 C、4 D、9. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题4分,共24分)把答案直接填在答题卡的相应位置处.
-
10. 某种水果的原价为15元/箱,经过连续两次增长后的售价为30元/箱.设平均每次增长的百分率为x , 根据题意列方程是 .11. 在一个不透明的布袋中装有30个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.4左右,则布袋中白球可能有个.12. 用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .13. 如图,点A在双曲线上,轴于B , 且的面积 , 则.
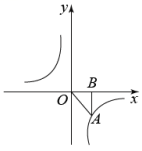 14. 如图,的直径垂直弦于点E , , , 则.
14. 如图,的直径垂直弦于点E , , , 则.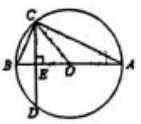 15. 二次函数的部分图象如图所示,对称轴为 , 图象过点A , 且 , 以下结论:①;②关于x的不等式的解集为:;③;④(m为任意实数);⑤若点 , 在此函数图象上,则.其中错误的结论是.
15. 二次函数的部分图象如图所示,对称轴为 , 图象过点A , 且 , 以下结论:①;②关于x的不等式的解集为:;③;④(m为任意实数);⑤若点 , 在此函数图象上,则.其中错误的结论是.
三、解答题(本大题共8小题,共90分)解答时应在答题卡的相应位置处写出文字说明、证明过程或演算过程.
-
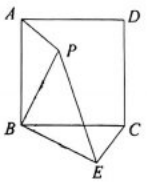
16. 解方程:(1)、;(2)、17. 关于x的一元二次方程有两个不相等的实数根.(1)、求m的取值范围;(2)、若方程有一个根为 , 求m的值和另一根.18. 如图,P是正方形内一点,绕着点B旋转后能到达的位置,若.求线段的长.
 19. 已知:二次函数中的x和y满足下表:
19. 已知:二次函数中的x和y满足下表:x
…
0
1
2
3
4
5
…
y
…
3
0
0
m
8
…
(1)、m的值为.(2)、求出这个二次函数的解析式;(3)、当时,则y的取值范围为.20. 如图,一次函数图象与x轴,y轴分别相交于A、B两点,与反比例函数的图象相交于点E、F , 已知点 , 点.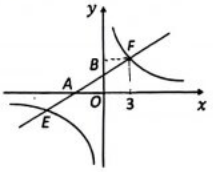 (1)、求一次函数和反比例函数的表达式;(2)、结合该图象直接写出满足不等式的解集.21. 为弘扬中华传统文化,“诵读经典,传承文明”,某学校近期举办了“国学经典诵读赛”,诵读的篇目分成四种类型:A.蒙学今诵;B.爱国传承;C.励志劝勉;D.愚公移山,每种类型的篇目数相同,参赛者需从这四种类型中随机抽取一种诵读类型.(1)、小颖参加了这次大赛,她恰好抽中“B.爱国传承”的概率是;(2)、小红和小迪也参加了这次大赛,请用画树状图或列表法求他们抽中同一种类型篇目的概率.
(1)、求一次函数和反比例函数的表达式;(2)、结合该图象直接写出满足不等式的解集.21. 为弘扬中华传统文化,“诵读经典,传承文明”,某学校近期举办了“国学经典诵读赛”,诵读的篇目分成四种类型:A.蒙学今诵;B.爱国传承;C.励志劝勉;D.愚公移山,每种类型的篇目数相同,参赛者需从这四种类型中随机抽取一种诵读类型.(1)、小颖参加了这次大赛,她恰好抽中“B.爱国传承”的概率是;(2)、小红和小迪也参加了这次大赛,请用画树状图或列表法求他们抽中同一种类型篇目的概率.
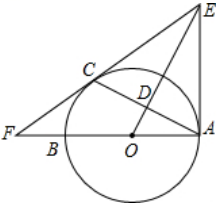
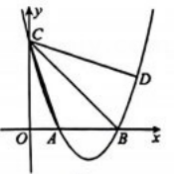 图2
图2 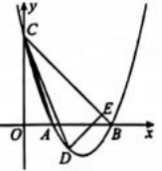 备用图
备用图