安徽省宿州市砀山县2023-2024学年七年级上学期数学月考考试试卷
试卷更新日期:2024-03-01 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 下列数中,是正整数的是( )A、 B、0 C、2023 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列方程中,是一元一次方程的是( )A、 B、 C、 D、4. 下列各图中表示线段 ,射线 的是( )A、
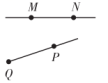
B、
B、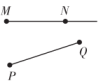
C、
C、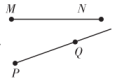
D、
D、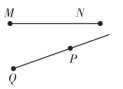
5. 下列等式变形,错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图是一个正方体的展开图,在原正方体中,与“梦”字所在面相对的面上的汉字是( )
5. 下列等式变形,错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图是一个正方体的展开图,在原正方体中,与“梦”字所在面相对的面上的汉字是( )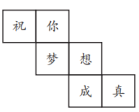 A、你 B、想 C、成 D、真7. 在下列现象中,体现了基本事实“两点确定一条直线”的有( )
A、你 B、想 C、成 D、真7. 在下列现象中,体现了基本事实“两点确定一条直线”的有( )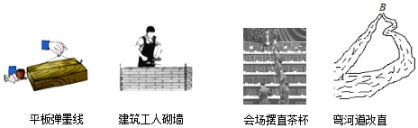 A、1个 B、2个 C、3个 D、4个8. 已知关于的方程的解是 , 则的值为( )A、 B、2 C、 D、69. 如图, , , 平分 , 则的度数是( )
A、1个 B、2个 C、3个 D、4个8. 已知关于的方程的解是 , 则的值为( )A、 B、2 C、 D、69. 如图, , , 平分 , 则的度数是( )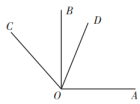 A、 B、 C、 D、10. 如图是一组有规律的图案,它们是由边长相同的灰白两种颜色的小正方形组成的,按照这样的规律,若组成的图案中有2025个灰色小正方形,则这个图案是( )
A、 B、 C、 D、10. 如图是一组有规律的图案,它们是由边长相同的灰白两种颜色的小正方形组成的,按照这样的规律,若组成的图案中有2025个灰色小正方形,则这个图案是( ) A、第505个 B、第506个 C、第507个 D、第508个
A、第505个 B、第506个 C、第507个 D、第508个二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 近四年来,安徽粮食综合生产能力稳定在800亿斤以上,800亿用科学记数法表示为 .12. 在半径为6cm的圆中,60°的圆心角所对的扇形面积等于cm2(结果保留π).13. 已知 , 则代数式 .14. 我们定义 , 如 , 若 , 则.
三、(本大题共2小题,每小题8分,满分16分)
-
15. 计算: .16. 解方程: .
四、(本大题共2小题,每小题8分,满分16分)
-
17. 先化简,再求值: , 其中 , .18. 如图,平面上有四个点A、B、C、D , 根据下列语句画图.
 (1)、画直线、直线交于点;(2)、画线段、线段交于点;(3)、作射线.
(1)、画直线、直线交于点;(2)、画线段、线段交于点;(3)、作射线.五、(本大题共2小题,每小题10分,满分20分)
-
19. 某中学七年级数学课外兴趣小组在探究:“边形共有多少条对角线”这一问题时,设计了如下表格:
多边形的边数
4
5
6
…
n
从多边形一个顶点出发可引起的对角线条数
1
2
3
…
____▲____
多边形对角线的总条数
2
5
9
…
▲
 (1)、请在表格中的横线上填上相应的结果;(2)、求十二边形总共有多少条对角线;(3)、过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为2016吗?若能,请求出这个多边形的边数;若不能,请说明理由.20. 某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用围网在水库中围成了如图所示的①、②、③三块长方形区域,其中区域①的一边长DF为a米,区域③长方形的长BC为b米,BC是其宽FC的4倍.
(1)、请在表格中的横线上填上相应的结果;(2)、求十二边形总共有多少条对角线;(3)、过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为2016吗?若能,请求出这个多边形的边数;若不能,请说明理由.20. 某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用围网在水库中围成了如图所示的①、②、③三块长方形区域,其中区域①的一边长DF为a米,区域③长方形的长BC为b米,BC是其宽FC的4倍.
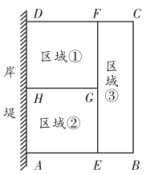 (1)、宽FC的长度为米;围成养殖场围网的总长度为米;(2)、当 , 时,求围网的总长度.
(1)、宽FC的长度为米;围成养殖场围网的总长度为米;(2)、当 , 时,求围网的总长度.六、(本题满分12分)
-
21. 如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=2cm.
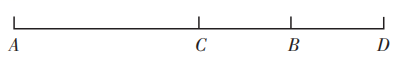 (1)、求AC的长(2)、若点E在直线AD上,且EA=3cm,求BE的长
(1)、求AC的长(2)、若点E在直线AD上,且EA=3cm,求BE的长七、(本题满分12分)
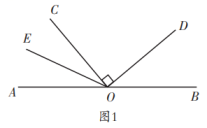 图2
图2