安徽省淮南市潘集区2023-2024学年八年级上学期数学第二次月考考试试卷

试卷更新日期：2024-03-01 类型：月考试卷

进入出卷网下载

一、选择题（本题共10小题，每小题3分，满分30分）

1. 下列运算正确的是（）

A、 $a^{8} \div a^{4} = a^{2}$ B、 $a^{2} \cdot a^{2} = a^{4}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 $(2 a)^{3} = 6 a^{3}$

查看试题解析
2. ${(\frac{1}{8})}^{101} \cdot 8^{100} =$ （）

A、 $\frac{1}{4}$ B、 $\frac{1}{8}$ C、4 D、8

查看试题解析
3. 要使 $(x^{2} + a x + 5) (x - b)$ 展开式中 $x^{2}$ 项的系数与常数项相等，都等于10，则a的值等于（）

A、 $- 6$ B、6 C、8 D、 $- 8$

查看试题解析
4. 长为9，7，5，3的四根木条，选其中三根组成三角形，有几种选法？（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
5. 在 $△ A B C$ 中，已知 $∠ A B C = 66 °$ ， $∠ A C B = 54 °$ ， BE是AC上的高，CF是AB上的高，H是BE和CF的交点， $∠ E H F$ 的度数是（）

A、 $50 °$ B、 $40 °$ C、 $130 °$ D、 $120 °$

查看试题解析
6. 如图，若△ABC≌△ADE，则下列结论中一定成立的是（）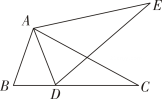

A、AC＝DE B、∠BAD＝∠CAE C、AB＝AE D、∠ABC＝∠AED

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = 8$ ， $A C = 6$ ， O为 $△ A B C$ 角平分线的交点，若 $△ A B O$ 的面积为20，则 $△ A C O$ 的面积为是（）

A、12 B、15 C、16 D、18

查看试题解析
8. 点 $P (5 ， - 4)$ 关于y轴的对称点的坐标是（）

A、 $(- 5 ， - 4)$ B、 $(5 ， 4)$ C、 $(- 5 ， 4)$ D、 $(5 ， - 4)$

查看试题解析
9. 如图，将长方形纸片ABCD ，沿折痕MV折叠，B分别落在 $A_{1}$ ， $B_{1}$ 的位置， $A_{1} B_{1}$ 交AD于点E ，若 $∠ B N M = 65 °$ ，以下结论：① $∠ B_{1} N C = 50 °$ ；② $∠ A_{1} M E = 50 °$ ；③ $A_{1} M ∥ B_{1} N$ ；④ $∠ D E B_{1} = 40 °$ ．正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图所示， $∠ A O B = 60 °$ ，点P是 $∠ A O B$ 内一定点，并且 $O P = 2$ ，点M、N分别是射线OA ， OB上异于点O的动点，当 $△ P M N$ 的周长取最小值时，点O到线段MN的距离为（）

A、1 B、2 C、4 D、1.5

查看试题解析

二、填空题（本题共6小题，每小题3分，满分18分）

11. 根据如图所示的计算程序计算变量y的值，若输入 $m = 3$ ， $n = 2$ 时，则输出y的值是．

查看试题解析
12. 计算： $- 5 x y (3 x^{2} - y^{2}) =$ ．

查看试题解析
13. 如图， $△ A B C$ 的两边AB ， AC的垂直平分线分别交BC于D、B ，若 $∠ B A C + ∠ D A E = 150 °$ ，则 $∠ B A C$ 的度数为．

查看试题解析
14. 与点 $(2 ， - 7)$ 关于y轴对称的点的坐标为，关于 $y = - 1$ 对称的点的坐标为．

查看试题解析
15. 如图，四边形ABCD中， $∠ A = 90 °$ ， $A D = 3$ ，连接BD ， $B D ⊥ C D$ ， $∠ A D B = ∠ C$ ，若P是BC边上一动点，则DP长的最小值为．

查看试题解析
16. 如图，在等腰直角三角形ABC中， $∠ C = 90 °$ ， $A C = B C = 4$ ，点D是AB的中点，E ， F分别在AC边与CB边上运动，且满足 $A E = C F$ ， $∠ E D F = 90 °$ ；当点E运动到与点C的距离为1时，则 $△ D E F$ 的面积为．

查看试题解析

三、解答题（共52分）

17. 计算

(1)、 $(2 x + 3 y) (x - y)$

(2)、 $(3 x^{2} y - 6 x y) \div 6 x y$

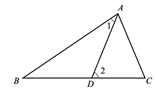
查看试题解析
18. 先化简．再求值： $(2 x + 1) (2 x - 1) - (x - 2)^{2} - (3 x^{3} + x^{2} - x) \div x$ ，其中 $x = - \frac{1}{3}$ ．

查看试题解析
19. 已知：如图所示，在△ABC中，D是BC边上一点，∠1=∠B，∠2=∠C，∠BAC=75°，求∠DAC的度数.

查看试题解析
20. 如图，点B ， F ， C ， E在同一直线上，AC ， DF相交于点M ， $∠ B = ∠ E$ ， $A B = D E$ ， $B F = C E$ ，求证： $∠ A C B = ∠ D F E$ ．

查看试题解析
21. 在如图的正方形网格中，每一个小正方形的边长为1；格点三角形ABC（顶点是网格线交点的三角形）的顶点A、C的坐标分别是 $(- 4 ， 6)$ ， $(- 1 ， 4)$ ．

(1)、请在图中的网格平面内建立平面直角坐标系；

(2)、请画出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(3)、请在y轴上求作一点P ，使 $△ P B_{1} C$ 的周长最小，并直接写出点P的坐标．

查看试题解析
22. 如图，在等边三角形ABC中，点P ， Q分别在AC ， BC上，且 $A P = C Q$ ， AQ与BP交于点M ，在BP上取一点N ，使 $M N = M Q$ ，连接NQ ．求证： $△ M N Q$ 是等边三角形．

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C$ ，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作 $△ A D E$ ，使 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接CE ．

(1)、如图1，当点D在线段CB上，且 $∠ B A C = 90 °$ 时，证明 $∠ D C E = 90 °$ ；

(2)、设 $∠ B A C = α$ ， $∠ D C E = β$ ．
①如图2，当点D在线段CB上， $∠ B A C \neq 90 °$ 时，请你直接写出 $α$ 与 $β$ 之间的数量关系；（无需证明）
②如图3，当点D在线段CB的延长线上， $∠ B A C \neq 90$ 时，写出此时 $α$ 与 $β$ 之间的数量关系并证明．

查看试题解析