安徽省宿州市砀山重点中学2023-2024学年八年级上学期数学月考考试试卷
试卷更新日期:2024-03-01 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分,每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的)
-
1. 实数0.618, , 0, , 中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个2. 二次根式中a的取值范围是( )A、 B、 C、 D、3. 下列各组数中,是勾股数的是( )A、0.3,0.4,0.5 B、1, , C、8,15,17 D、5,10,134. 已知二元一次方程组则的值是( )A、 B、 C、 D、95. 已知点与点关于y轴对称,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列计算正确的是( )A、 B、 C、 D、7. 某学校规定学生的学期综合成绩满分为100分,将平时成绩、期中成绩、期末成绩按的比例计算综合成绩.小欢同学本学期的三项成绩(百分制)分别为95分、90分、85分.则小欢同学本学期的综合成绩是( )A、87分 B、89分 C、90分 D、92分8. 2023年9月26日,第十四届中国(合肥)国际园林博览会正式开幕,吉祥物“小喜”因其灵动可爱的形象受到了大家的喜爱.为了提高销量,某店家推出了吉祥物套装礼盒,一个套装礼盒里包含1个吉祥物玩偶和2个钥匙扣.已知一个玩偶的进价为60元,一个钥匙扣的进价为20元,该店家计划用5000元购进一批玩偶和钥匙扣,使得刚好配套.设购进x个玩偶,y个钥匙扣,则下列方程组正确的是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,已知点A在y轴上,轴于点C , 点A关于直线的对称点D恰好在上,点E与点O关于直线对称,且 , 则的度数为( )
 A、 B、 C、 D、10. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点P在线段上,轴于点C , 则周长的最小值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点P在线段上,轴于点C , 则周长的最小值为( )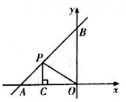 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若点在x轴上,则a的值为.12. 如果最简二次根式与是同类二次根式,那么x的值为.13. 若一次函数的图象向下平移3个单位长度后经过点 , 则平移后的一次函数表达式是.14. 若a , b都是实数,且满足 , 我们就称点为“和谐点”..(1)、若点是“和谐点”,则c的值是.(2)、已知以关于x , y的方程组的解为坐标的点是“和谐点”,则m的值为.
三、(本大题共2小题,每小题8分,满分16分)
-
15. 计算:.16. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
 (1)、作出关于y轴对称的;(2)、求的面积.
(1)、作出关于y轴对称的;(2)、求的面积.四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图在四边形ABCD中,AB=BC=2,CD=3,DA=1,且∠B=90°,求∠DAB的度数.
 18. 2023年10月26日,神舟十七号载人飞船与空间站组合体完成自主快速交会对接,神舟十七号发射取得圆满成功,极大地激发了学生们学习航空航天知识的热情.某学校在此背景下组织了一次“航空航天知识”系列活动.下面是八年级甲、乙两个班各项目的成绩(单位:分).
18. 2023年10月26日,神舟十七号载人飞船与空间站组合体完成自主快速交会对接,神舟十七号发射取得圆满成功,极大地激发了学生们学习航空航天知识的热情.某学校在此背景下组织了一次“航空航天知识”系列活动.下面是八年级甲、乙两个班各项目的成绩(单位:分).知识竞赛
演讲比赛
手抄报
甲
85
91
88
乙
90
84
87
(1)、如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲,乙两班谁将获胜;(2)、如果将知识竞赛、演讲比赛、手抄报按的比例确定最后成绩,请通过计算说明甲、乙两班谁将获胜.五、(本大题共2小题,每小题10分,满分20分)
-
19. 已知a , b , c是的三边长.(1)、化简:;(2)、若 , 求的周长.20. 如图,已知直线经过点和点 , 点C在线段上,将沿折叠后,点O恰好落在边上点D处.
 (1)、求直线的表达式;(2)、求的面积.
(1)、求直线的表达式;(2)、求的面积.六、(本题满分12分)
-
21. 阅读探索:
材料一:解方程组时,采用了一种“换元法”的解法,解法如下:
解:设 , , 原方程组可化为解得
即解得
材料二:解方程组时,采用了一种“整体代换”的解法,解法如下
解:将方程②变形为③,把方程①代入③得, , 则;把代入①得, , 所以方程组的解为
根据上述材料,解决下列问题:
(1)、运用换元法解关于a , b的方程组(2)、若关于x , y的方程组的解为求关于m , n的方程组的解;(3)、已知x , y , z满足试求z的值.七、(本题满分12分)
-
22. 某汽车销售公司计划购进一批新能源汽车进行试销售,据了解1辆甲型新能源汽车、3辆乙型新能源汽车的进价共计55万元;4辆甲型新能源汽车、2辆乙型新能源汽车的进价共计120万元.(1)、求甲、乙两种型号的新能源汽车每辆的进价分别为多少万元?(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的新能源汽车均购买),通过计算求出该公司全部的购买方案;(3)、若该汽车销售公司销售1辆甲型新能源汽车可获利9000元,销售1辆乙型新能源汽车可获利4000元,在(2)的购买方案中,若每种方案中的新能源汽车均全部售出,请问哪种方案获利最大,最大利润为多少?
八、(本题满分14分)
-
23. 如图1,已知直线与y轴交于点A , 与x轴交于点 , 直线以每秒1个单位长度的速度沿y轴正方向平移,平移时交线段于点D , 交线段于点C , 当点C与点B重合时结束运动.
 (1)、求k的值;(2)、若直线的函数关系式为 , P是直线上一点,当时,求点P的坐标;(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为.当时,求t的值.
(1)、求k的值;(2)、若直线的函数关系式为 , P是直线上一点,当时,求点P的坐标;(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为.当时,求t的值.
-
-