江西省丰城重点中学2023-2024学年九年级上学期数学月考考试试卷(12月)
试卷更新日期:2024-03-01 类型:月考试卷
一、选择题
-
1. |﹣3|的绝对值为( )A、﹣3 B、0 C、3 D、±32. 如图,几何体的主视图是( )
 A、
A、 B、
B、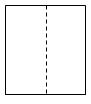 C、
C、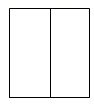 D、
D、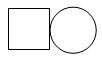 3. 新冠疫情防控形势下,学校要求学生每日测量体温.某同学连续一周的体温情况如表所示,则该同学这一周的体温数据的众数和中位数分别是( )
3. 新冠疫情防控形势下,学校要求学生每日测量体温.某同学连续一周的体温情况如表所示,则该同学这一周的体温数据的众数和中位数分别是( )日期
星期一
星期二
星期三
星期四
星期五
星期六
星期天
体温(℃)
36.3
36.7
36.2
36.3
36.2
36.4
36.3
A、36.3和36.2 B、36.2和36.3 C、36.3和36.3 D、36.2和36.14. 二次函数y=ax2+bx+c的图象如图所示,下列说法错误的是( ) A、a<0,b>0 B、b2﹣4ac>0 C、方程ax2+bx+c=0的解是x1=5,x2=﹣1 D、不等式ax2+bx+c>0的解集是0<x<55. 不等式组的解集在以下数轴表示中正确的是( )A、
A、a<0,b>0 B、b2﹣4ac>0 C、方程ax2+bx+c=0的解是x1=5,x2=﹣1 D、不等式ax2+bx+c>0的解集是0<x<55. 不等式组的解集在以下数轴表示中正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
6. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )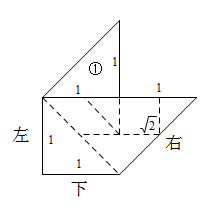 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 因式分解:m2﹣3m= .8. 已知一次函数y=ax-1,若y随x的增大而减小,则它的图象不经过第象限.9. “一带一路”涉及沿线65个国家,总涉及人口约4500000000人,将4500000000用科学记数法表示为 .10. 已知方程的两根,那么的值是 .11. 社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示,经分析可以推断盒子里个数比较多的是(填“黑球”或“白球”).
 12. 如图,腰长为22的等腰ABC中,顶角∠A=45°,D为腰AB上的一个动点,将ACD沿CD折叠,点A落在点E处,当CE与ABC的某一条腰垂直时,BD的长为 .
12. 如图,腰长为22的等腰ABC中,顶角∠A=45°,D为腰AB上的一个动点,将ACD沿CD折叠,点A落在点E处,当CE与ABC的某一条腰垂直时,BD的长为 .
三、解答题(本大题5小题,每小题6分,共30分)
-
13.(1)、;(2)、如图,在中, , , , 将绕点A逆时针旋转得到 , 并使点落在边上,连接 , 求的长.
 14. 先化简,再求值: , 其中是方程的解.15. 如图,在下列的正方形网格中,的顶点A , B , C均在格点上,请仅用无刻度直尺按下列要求作图(保留作图痕迹).
14. 先化简,再求值: , 其中是方程的解.15. 如图,在下列的正方形网格中,的顶点A , B , C均在格点上,请仅用无刻度直尺按下列要求作图(保留作图痕迹). (1)、在图1中,在边上找一点P , 连接 , 使;(2)、在图2中,在边上找一点Q , 连接 , 使 .16. 如图,一次函数与反比例函数的图象交于 , 两点.
(1)、在图1中,在边上找一点P , 连接 , 使;(2)、在图2中,在边上找一点Q , 连接 , 使 .16. 如图,一次函数与反比例函数的图象交于 , 两点. (1)、求一次函数的解析式;(2)、求的面积.17. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
(1)、求一次函数的解析式;(2)、求的面积.17. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.
(1)、求证: .(2)、若 , , 求阴影部分的面积.四、(本大题3小题,每小题8分,共24分)
-
18. 2022年北京冬季奥运会吉祥物冰墩墩大受欢迎.某商店第一次用4000元购进某款冰墩墩纪念章,很快卖完.第二次又用3000购进该款纪念章,但这次每个纪念章是第一次进价的1.2倍,数量比第一次少了30个.(1)、求第一次每个纪念章的进价是多少元?(2)、若第二次进货后按80元/个的价格出售,恰好销售完一半时,根据市场情况,商店决定对剩余的纪念章按同一标准一次性打折销售,但要求这次的利润不少于600元,问最低可打几折?19. 如图1是一个长方体形家用冰箱,长宽高分别为0.5米,0.5米,1.7米,在搬运上楼的过程中,由于楼梯狭窄,完全靠一名搬运师傅背上楼.
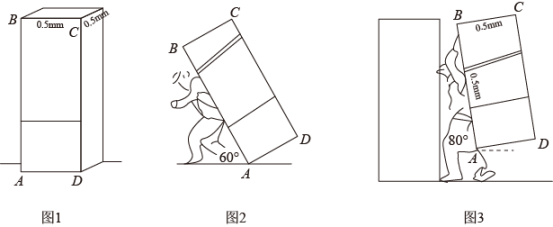 (1)、如图2,为便于搬运师傅起身,冰箱通常与地面成60°角,求此时点D与地面的高度;(2)、如图3,在搬运过程中,冰箱与水平面成80°夹角,最低点A与地面高度为0.3米,门的高度为2米,假如最高点C与门高相同时,刚好可以搬进去.若他保持冰箱与平面夹角不变,他要下蹲几厘米(结果保留整数)才刚好进门?(sin80°≈0.98,cos80°≈0.16,tan80°≈5.67)20. 某校开展课后延时服务,计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组,由于师资等条件的限制,每人只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题:
(1)、如图2,为便于搬运师傅起身,冰箱通常与地面成60°角,求此时点D与地面的高度;(2)、如图3,在搬运过程中,冰箱与水平面成80°夹角,最低点A与地面高度为0.3米,门的高度为2米,假如最高点C与门高相同时,刚好可以搬进去.若他保持冰箱与平面夹角不变,他要下蹲几厘米(结果保留整数)才刚好进门?(sin80°≈0.98,cos80°≈0.16,tan80°≈5.67)20. 某校开展课后延时服务,计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组,由于师资等条件的限制,每人只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题: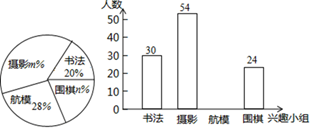 (1)、求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、求扇形统计图中,“摄影”对应扇形圆心角的度数;(4)、若该校共有1200名学生参加课后延时服务,试估计该校选择“围棋”课外兴趣小组的学生有多少人?
(1)、求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、求扇形统计图中,“摄影”对应扇形圆心角的度数;(4)、若该校共有1200名学生参加课后延时服务,试估计该校选择“围棋”课外兴趣小组的学生有多少人?五、(本大题2小题,每小题9分,共18分)
-
21. 二次函数的图象交轴于原点及点 .
 (1)、感知特例:
(1)、感知特例:当时,如图1,抛物线上的点 , , , , 分别关于点中心对称的点为 , , , , , 如下表:
…
( ▲ , ▲)
…
…
…
①补全表格:A ( ▲ , ▲)
②请在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
(2)、形成概念:
我们发现形如(1)中的图象上的点和抛物线上的点关于点中心对称,则称是的“孔像抛物线”.例如,当时,图2中的抛物线是抛物线的“孔像抛物线”.
探究问题①当时,若抛物线与它的“孔像抛物线”的函数值都随着的增大而减小,则的取值范围为 ▲;
②若二次函数及它的“孔像抛物线”与直线有且只有三个交点,求的值.
22. 综合与实践如图1,已知点G在正方形ABCD的对角线AC 上,GE⊥BC , 垂足为E , GF⊥CD , 垂足为F .
 (1)、【证明与推断】
(1)、【证明与推断】①四边形CEGF的形状是 ▲;
②的值为 ▲;
(2)、【探究与证明】在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)、【拓展与运用】如图3,在(2)的条件下,正方形CEGF 在旋转过程中,当B、E、F三点共线时,探究AG和GE的位置关系,并说明理由.
六、解答题(本小题12分)
-
23. 如图,平面直角坐标系中,O是坐标原点,直线经过点 , 与x轴交于点A , 与y轴交于点B.线段平行于x轴,交直线于点D , 连接 , .
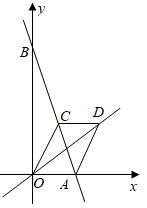 (1)、填空: . 点A的坐标是;(2)、求证:四边形是平行四边形;(3)、动点P从点O出发,沿对角线以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.
(1)、填空: . 点A的坐标是;(2)、求证:四边形是平行四边形;(3)、动点P从点O出发,沿对角线以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.①当时,求的面积
②当点P , Q运动至四边形为矩形时,请求出此时t的值.