江西省南昌市重点学校2023-2024学年九年级上学期月考数学试题
试卷更新日期:2024-03-01 类型:月考试卷
一、选择题(本题共6小题,每小题3分,共18分)
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 如图,△ 内接于⊙O, 是⊙O的直径,∠ .则∠ 的度数是 ( )
 A、36° B、33° C、30° D、27°3. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、4. 如图是三个反比例函数 , , 的图象,由此观察得到 , , 的大小关系为( )
A、36° B、33° C、30° D、27°3. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、4. 如图是三个反比例函数 , , 的图象,由此观察得到 , , 的大小关系为( ) A、 B、 C、 D、5. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则 的长为( )
A、 B、 C、 D、5. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则 的长为( )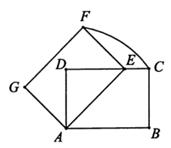 A、 B、 C、 D、π6. 如图,抛物线与轴交于点 , 其对称轴为直线 , 结合图象分析下列结论:
A、 B、 C、 D、π6. 如图,抛物线与轴交于点 , 其对称轴为直线 , 结合图象分析下列结论:①;②当时,y随x的增大而增大;③一元二次方程的两根分别为 , ;④若 , 为方程的两个根,则且;⑤ , 其中正确的结论有( )个
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本题共6小题,每小题3分,共18分)
-
7. 抛物线 的顶点坐标是.8. 如图,正比例函数与反比例函数的图象相交于A,C两点,过A作x轴的垂线交x轴于B,连接BC,若的面积为3,则k的值为 .
 9. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 .
9. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 . 10. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .11. 如图,在中, , , , 则的内切圆半径 .
10. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .11. 如图,在中, , , , 则的内切圆半径 . 12. 如图,已知是等腰直角三角形, , 将线段AC绕点A逆时针旋转得到 , 连接 , . 当是等腰三角形(不含等腰直角三角形)时, .
12. 如图,已知是等腰直角三角形, , 将线段AC绕点A逆时针旋转得到 , 连接 , . 当是等腰三角形(不含等腰直角三角形)时, .
三、解答题(本大题共5小题,每小题6分,共30分)
-
13.(1)、解下列方程: .(2)、如图,的半径 , 于点C, , 求的长.
 14. 按要求画图:①仅用无刻度的直尺;②保留必要的画图痕迹.
14. 按要求画图:①仅用无刻度的直尺;②保留必要的画图痕迹.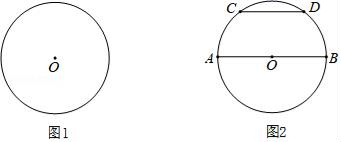 (1)、如图1,画出⊙O的一个内接矩形;(2)、如图2,AB是⊙O的直径,CD是⊙O的弦,且CD∥AB,画出⊙O的一个内接正方形.15. 已知关于x的一元二次方程.(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰的一边长 , 另两边长b、c恰好是这个方程的两个根,求k的值.16. 为了迎接明年南昌五中七十周年校庆,政教处组织开展“校史知识竞赛”,某班准备从甲、乙2名女生和丙、丁2名男生中任选2人代表班级参加比赛.(1)、如果已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是 .(2)、用列表法或树状图法表示出所选代表的所有可能结果,并求出所选代表恰好为1名女生和1名男生的概率.17. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)、如图1,画出⊙O的一个内接矩形;(2)、如图2,AB是⊙O的直径,CD是⊙O的弦,且CD∥AB,画出⊙O的一个内接正方形.15. 已知关于x的一元二次方程.(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰的一边长 , 另两边长b、c恰好是这个方程的两个根,求k的值.16. 为了迎接明年南昌五中七十周年校庆,政教处组织开展“校史知识竞赛”,某班准备从甲、乙2名女生和丙、丁2名男生中任选2人代表班级参加比赛.(1)、如果已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是 .(2)、用列表法或树状图法表示出所选代表的所有可能结果,并求出所选代表恰好为1名女生和1名男生的概率.17. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题: (1)、求y与的函数表达式;(2)、大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?(3)、若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?
(1)、求y与的函数表达式;(2)、大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?(3)、若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?四、解答题(本题共3小题,每小题8分,共24分)
-
18. 某中学积极推进校园文学创作,倡导每名学生每学期向校报编辑部至少投1篇稿件.学期末,学校对七、八年级的学生投稿情况进行调查.
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生,统计每人在本学期投稿的篇数,制作了频数分布表.
投稿篇数(篇)
1
2
3
4
5
七年级频数(人)
7
10
15
12
6
八年级频数(人)
2
10
13
21
4
(1)、【数据的描述与分析】
求扇形统计图中圆心角的度数,并补全频数直方图. (2)、根据频数分布表分别计算有关统计量:
(2)、根据频数分布表分别计算有关统计量:统计量
中位数
众数
平均数
方差
七年级
3
3
八年级
直接写出表格中 ▲ , ▲ , 并求出 .
(3)、【数据的应用与评价】
从中位数、众数、平均数、方差中,任选两个统计量,对七、八年级学生的投稿情况进行比较,并做出评价.19. 有这样一个问题:探究函数的图象与性质.小丽根据学习函数的经验,对函数的图象与性质进行了探究.
下面是小丽的探究过程,请补充完整:
(1)、函数的自变量x的取值范围是 .(2)、如图,在平面直角坐标系xOy中,画出了函数的部分图象,用描点法将这个函数的图象补充完整; (3)、对于上面的函数 , 下列四个结论:
(3)、对于上面的函数 , 下列四个结论:①函数图象关于y轴对称;函数既有最大值,也有最小值;
③当时,y随x的增大而增大,当时,y随x的增大而减小;
④函数图象与x轴有2个公共点.
所有正确结论的序号是 .
(4)、结合函数图象,解决问题:若关于x的方程有4个不相等的实数根,则k的取值范围是 .
20.(1)、知识重现:如图1,我们已经分三种情况探究了一条弧所对的圆周角和它所对的圆心角的数量关系.
图1
①直接写出和的数量关系 ▲ .
②任选一种情况进行证明.
(2)、迁移应用:如图2,已知内接于 , 直线DE是切线,切点为A,求证: .
图2
五、解答题(本题共两小题,每小题9分,共18分)
-
21. 如图,线段AB经过的圆心O,交于A、C两点, , AD为的弦,连接BD, , 连接DO并延长交于点E,连接BE交于点M.
 (1)、求证:直线BD是的切线;(2)、求封闭图形BCD的面积;(3)、求线段BM的长.22. 2023年杭州亚运会吉祥物一经开售,就深受大家的喜爱,某商店以每件45元的价格购进某款亚运会吉祥物,以每件68元的价格出售,经统计,2023年5月份的销售量为256件,2023年7月份的销售量为400件.(1)、求该款吉祥物2023年5月份到7月份销售量的月平均增长率.(2)、从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该款吉祥物每降价1元,月销售量就会增加20件.设该款吉祥物每件降价m元(m为正整数),当m为多少时,月销售利润能达到8400元?(3)、在(2)的条件下,设该款吉祥物每月销售利润为w元,当m为多少时,月销售利润最大?最大利润是多少元?
(1)、求证:直线BD是的切线;(2)、求封闭图形BCD的面积;(3)、求线段BM的长.22. 2023年杭州亚运会吉祥物一经开售,就深受大家的喜爱,某商店以每件45元的价格购进某款亚运会吉祥物,以每件68元的价格出售,经统计,2023年5月份的销售量为256件,2023年7月份的销售量为400件.(1)、求该款吉祥物2023年5月份到7月份销售量的月平均增长率.(2)、从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该款吉祥物每降价1元,月销售量就会增加20件.设该款吉祥物每件降价m元(m为正整数),当m为多少时,月销售利润能达到8400元?(3)、在(2)的条件下,设该款吉祥物每月销售利润为w元,当m为多少时,月销售利润最大?最大利润是多少元?六、解答题(本题共1题,共12分)
-
23. 如图1,中, , , 为内一点,将绕点按逆时针方向旋转角得到 , 点 , 的对应点分别为点 , , 且 , , 三点在同一直线上.
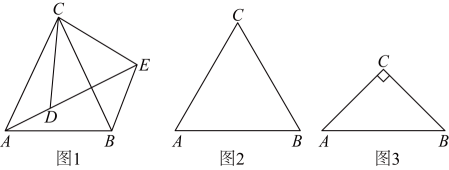 (1)、填空:;(用含α的代数式表示)(2)、如图2,若 , 请补全图形,再过点作于点 , 然后探究线段 , , 之间的数量关系,并证明你的结论;(3)、如图3,若 , , 求四边形面积的最大值.
(1)、填空:;(用含α的代数式表示)(2)、如图2,若 , 请补全图形,再过点作于点 , 然后探究线段 , , 之间的数量关系,并证明你的结论;(3)、如图3,若 , , 求四边形面积的最大值.