【培优卷】2024年浙教版数学七年级下册第2章二元一次方程组单元测试

试卷更新日期：2024-03-01 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如果方程组 ${\begin{cases} a x - b y =13 \\ 4x-5y=41 \end{cases}$ 与 ${\begin{cases} a x + b y =3 \\ 2x+3y=-7 \end{cases}$ 有相同的解，则a，b的值是（）

A、 ${\begin{cases} a = 2 \\ b = 1 \end{cases}$ B、 ${\begin{cases} a = 2 \\ b = - 3 \end{cases}$ C、 ${\begin{cases} a = \frac{5}{2} \\ b = 1 \end{cases}$ D、 ${\begin{cases} a = 4 \\ b = - 5 \end{cases}$

查看试题解析
2. 已知关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = 21 \\ a_{2} x + b_{2} y = 12 \end{array}$ 的解是 ${\begin{array}{l} x = 3 \\ y = 6 \end{array}$ ，则关于 $m$ 和 $n$ 的方程组 ${\begin{array}{l} a_{1} (2 m + n) + b_{1} (m - n) = 21 \\ a_{2} (2 m + n) + b_{2} (m - n) = 12 \end{array}$ 的解是（）

A、 ${\begin{array}{l} m = 3 \\ n = 6 \end{array}$ B、 ${\begin{array}{l} m = 3 \\ n = - 3 \end{array}$ C、 ${\begin{array}{l} m = 2 \\ n = 3 \end{array}$ D、 ${\begin{array}{l} m = 2 \\ n = - 3 \end{array}$

查看试题解析
3. 如图，将9个不同的数填在3×3的方格中，使得每行、每列、每条对角线上的三个数字之和均相等，以下方程组符合题意的是（）．

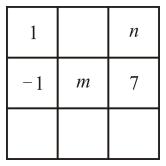A、 ${\begin{array}{l} 1 + n = - 1 + m + 7 \\ m + n = 7 + n \end{array}$ B、 ${\begin{array}{l} m + n = 1 - 1 \\ 1 + m = n + 7 \end{array}$ C、 ${\begin{array}{l} 1 + n = - 1 + m + 7 \\ 1 + m = n + 7 \end{array}$ D、 ${\begin{array}{l} m + n = 1 - 1 \\ m + n = 7 + n \end{array}$

查看试题解析
4. 已知关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{cases}$ ，则下列结论中正确的是（）
①当a=5时，方程组的解是 ${\begin{cases} x = 10 \\ y = 20 \end{cases}$
②当x，y的值互为相反数时，a=20．
③不存在一个实数a使得x=y．
④若2^2a-3y=2⁷ ，则a=2．

A、①②④ B、①②③ C、②③④ D、②③

查看试题解析
5. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，不同的截法有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
6. 公式s=s₀+vt表示的是路程s与时间t之间的关系（其中s_0，v都是不等于零的常数），且当t=5时，s=260；当t=7时，s=340，则s_0，v的值分别是（）

A、s₀=60，v=40 B、s₀=-60，v=40 C、s₀=60，v=-40 D、s₀=-60，v=-40

查看试题解析
7. 如图，在周长为60的大长方形ABCD中放入六个相同的小长方形，若每个小长方形的面积为S，长为x，宽为y，则（）

A、当x=2时，S=20 B、当y=2时，S=20 C、当x=2y时，S=10 D、当x=4y时，S=10

查看试题解析
8. 小虎、大壮和明明三人玩飞镖游戏，各投5支镖，规定在同一环内得分相同，中靶和得分情况如图，则大壮的得分是（）

A、20 B、22 C、23 D、25

查看试题解析
9. 计算机的某种运算程序如图：

已知输入3时输出的运算结果是5，输入4时输出的运算结果是7．若输入的数是x（x≠0）时输出的运算结果为P ，输入的数是3x时输出的运算结果为Q ，则（）

A、P：Q＝3 B、Q：P＝3 C、（Q﹣1）：（P﹣1）＝3 D、（Q+1）：（P+1）＝3

查看试题解析
10. 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费=第一阶梯电费+第二阶梯电费）.规定：每月用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费. 如图是张磊家2021年9月和10月所交电费的收据，则该市规定的第一阶梯电价和第二阶梯电价分别为每度（）
代收电费收据

2021年9月

电表号

1205

户名

张磊

月份

9月

用电量

220度

金额

112元

代收电费收据

2021年10月

电表号

1205

户名

张磊

月份

10月

用电量

265度

金额

139元

A、0.5元，0.6元 B、0.4元，0.5元 C、0.3元，0.4元 D、0.6元，0.7元

查看试题解析

二、填空题（每题4分，共24分

11. 若关于x，y的方程组 ${\begin{array}{l} 3 x + y = k - 6 \\ x + 3 y = 2 \end{array}$ 的解满足 $x + y > 0$ ，则 $k$ 的取值范围是.

查看试题解析
12. 如图，射线OC的端点O在直线AB上，已∠1比∠2的2倍多10°，设∠1=x°，∠2=y°，则列出关于x，y的方程组是：.

查看试题解析
13. 在长方形ABCD中，放入六个形状、大小相同的小长方形，所标尺寸如图所示，则图中阴影部分的面积为cm².

查看试题解析
14. 冰墩墩和雪容融到校门外文具店买文件，冰墩墩购铅笔2支，练习本2本，圆珠笔1支，共付9元钱；雪容融购同样铅笔1支，练习本4本，圆珠笔2支，共付12元钱，若小明去购买与她们一样的铅笔1支、练习本2本、圆珠笔1支，他需付元钱.

查看试题解析
15. 已知关于x，y的方程组 $\{\begin{matrix} x + 2 y = k ， \\ 2 x + 3 y = 3 k - 1 ， \end{matrix}$ 有以下结论：
①当k=0时，方程组的解为 $\{\begin{matrix} x = - 2 ， \\ y = 1 ； \end{matrix}$ ②方程组的解可表示为 $\{\begin{matrix} x = 3 k - 2 ， \\ y = 1 - k ； \end{matrix}$ ③不论k取什么实数，x+3y的值始终不变.
其中正确的是（填序号）.

查看试题解析
16. 某校七年级有甲、乙、丙三个班，甲班比乙班多4名女姓，乙班比丙班多1名女姓．如果把甲班的第一组调到乙班，乙班的第一组调到丙班，丙班的第一组调到甲班，那么三个班的女生人数恰好相等．已知丙班第一组共有2名女生，则甲班第一组有名女生，乙班第一组有名女生．

查看试题解析

三、解答题（共8题，共66分）

17. 阅读材料：小明在解二元一次方程组 ${\begin{array}{l} a + b - 1 = 0 ① \\ 4 (a + b) - b = 5 ② \end{array}$ 时采用了一种“整体代换”的解法：
解：由①，得： $a + b = 1$ ③

将③代入②得， $4 \times 1 - b = 5$ ，即 $b = - 1$ ，

把 $b = - 1$ 代入③，得 $a = 2$ ．

∴方程组的解为 ${\begin{array}{l} a = 2 \\ b = - 1 \end{array}$ ．

请你模仿小明的方法，解决下列问题：

(1)、若 $2 x + y = 3$ ，则 $6 x + 3 y =$ 　　．

(2)、解方程 ${\begin{array}{l} x - 2 y + 4 = 0 \\ 2 x - 4 y + 3 y = 1 \end{array}$ ；

(3)、已知关于x、y的方程组 ${\begin{array}{l} 3 x^{2} - 2 x y + 9 y^{2} = 47 \\ 2 x^{2} - x y + 6 y^{2} = 36 \end{array}$ ，求 $x^{2} + 3 y^{2}$ 的值．

查看试题解析
18. 为提高病人免疫力，某医院精选甲、乙两种食物为病人配制营养餐．已知每克甲种食物中铁的含量是蛋白质的2倍，每克乙种食物中铁的含量是蛋白质的 $\frac{4}{7}$ ．

(1)、设每克甲种食物中含蛋白质x个单位，每克乙种食物中含蛋白质y个单位，请用含x ， y的式子填表：

每克甲种食物
每克乙种食物
蛋白质的含量/单位
x
y
铁的含量/单位
▲
▲

(2)、如果病人每餐需要175个单位的蛋白质和200个单位的铁，每餐需要甲、乙两种食物分别为140克，150克，求每克甲种食物中含蛋白质、铁各多少个单位．

查看试题解析

19. 声音在空气中传播的速度随温度的变化而变化，科学家已测得一定温度下声音传播的速度如下表．如果用

v

表示声音在空气中的传播速度，

t

表示温度，则

v

，

t

满足公式：

v = a t + b

（

a

，

b

为已知数）．

温度 $(℃)$	$- 20$	$- 10$	$0$	$10$	$20$
声音传播速度（米/秒）	$324$	$330$	$336$	$342$	$348$

(1)、求

a

，

b

的值．

(2)、若温度是

80 ℃

时，求声音在空气中的传播速度．

查看试题解析

20. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．

(1)、求每台A型电脑和B型电脑的销售利润：

(2)、商场计划在暑假期间，对A型电脑按成本价提高20%后标价，又以9折（即按标价的90%）优惠卖出，结果每台电脑仍可获利90元，则每台A型电脑的成本是多少元？

查看试题解析

21. 水是生命之源，“节约用水，人人有责”．为了加强公民的节水意识，合理利用水资源，我市居民生活用水按阶梯式水价计费，下表是该市居民“一户一表”生活用水及阶梯计费价格表的部分信息（注：水费按月份结算，

m^{3}

表示立方米）

每户每月用水量 $(m^{3})$	自来水销售价格（元 $/ m^{3}$ ）	污水处理价格（元 $/ m^{3}$ ）
不超出 $6 m^{3}$ 部分	$a$	1.10
超出 $6 m^{3}$ 不超出 $10 m^{3}$ 的部分	$b$	1.10
超出 $10 m^{3}$ 的部分	7.00	1.10

（注：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费用）．

已知2023年三月份，小红家用水 $8 m^{3}$ ，交水费32.8元，小智家用水 $10 m^{3}$ ，交水费44元．

(1)、请你根据以上信息，求表中a，b的值：

(2)、由于七月份正值夏天，小红家预计用水

15 m^{3}

，求小红家七月份预计应缴水费多少元？

(3)、若小智家四、五月份共用水

20 m^{3}

，其中四月份的用水量低于五月份的用水量，共缴水费89元，则小智家四、五月份的用水量各是多少？

查看试题解析

22. 如图，A，B两地有公路和铁路相连，在这条路上有一家食品厂，它到B地的距离是到A地的2倍，这家厂从A地购买原料，制成食品卖到B地．已知公路运价为1.5元/（公里·吨），铁路运价为1元/（公里·吨），这两次运输（第一次：A地→食品厂第二次：食品厂→B地）共支付公路运费15600元，铁路运费20600元．

(1)、这家食品厂到A地的距离是多少公里？

(2)、此次购进了多少吨原料？制成了多少吨食品

(3)、这家食品厂准备再新进一批原料，加工成食品后全部卖出，已知买进的原料每吨5000元，卖出的食品每吨10000元，保持原料产出食品的效率不变，如果希望获得利润不少于1122940元，则至少要购进多少吨原料？（注：利润＝销售款－原料费－运输费）

查看试题解析
23. 我市某包装生产企业承接了一批上海世博会的礼品盒制作业务，为了确保质量，该企业进行试生产．他们购得规格是 $170 c m \times 40 c m$ 的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材．如图甲，（单位： $c m$ ）

(1)、列出方程（组），求出图甲中a与b的值；

(2)、在试生产阶段，若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图乙的竖式与横式两种礼品盒．
①两种裁法共产生A型板材 ▲ 张，B型板材 ▲ 张；
②已知①中的A型板材和B型板材恰好做成竖式有盖礼品盒x个，横式无盖礼品盒的y个，求x、y的值．

查看试题解析
24. 【方法体验】已知方程组 ${\begin{matrix} 2018 x - 2017 y = 20 ， ① \\ 2019 x + 2018 y = 500. ② \end{matrix}$ 求4037x＋y的值．小明同学发现解此方程组代入求值很麻烦!后来他将两个方程直接相加便迅速解决了问题．请你体验一下这种快捷思路，写出具体解题过程：
【方法迁移】根据上面的体验，填空：

已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 则3x＋y－z＝．

【探究升级】已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 求－2x＋y＋4z的值．小明凑出

“－2x＋y＋4z＝2•（x＋2y＋3z）＋（－1）•（4x＋3y＋2z）＝20－15＝5”，虽然问题获得解决，但他觉得凑数字很辛苦!他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设－2x＋y＋4z＝m•（x＋2y＋3z）＋n•（4x＋3y＋2z），对照方程两边各项的系数可列出方程组 ${\begin{matrix} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{matrix}$ ，它的解就是你凑的数!

根据丁老师的提示，填空：

2x＋5y＋8z＝（x＋2y＋3z）＋（4x＋3y＋2z）

【巩固运用】已知2a－b＋kc＝4，且a＋3b＋2c＝－2，当k为时，8a＋3b－2c为定值，此定值是．（直接写出结果）

查看试题解析

电表号	1205
户名	张磊
月份	9月
用电量	220度
金额	112元

	每克甲种食物	每克乙种食物
蛋白质的含量/单位	x	y
铁的含量/单位	▲	▲

【培优卷】2024年浙教版数学七年级下册第2章二元一次方程组 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分

三、解答题（共8题，共66分）

【培优卷】2024年浙教版数学七年级下册第2章二元一次方程组单元测试