2024年高考物理二轮专题复习：动能定理及应用
试卷更新日期：2024-02-26 类型：二轮复习
一、选择题
-
1. 如图所示，小球滑离水平桌面到落地前，它的动能、重力势能、机械能E、速率v随下降高度h的变化关系，不计空气阻力，取水平地面为零势能面，正确的是（ ）
A、
B、
C、
D、
2.如图所示，虚线为某点电荷电场的等势面，现有两个比荷(即电荷量与质量之比)相同的带电粒子(不计重力)以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动，则可判断( )
A、两个粒子电性相同 B、经过b、d两点时，两粒子的加速度相同 C、经过b、d两点时，两粒子的速率相同 D、经过c、e两点时，两粒子的速率相同3. 从地面竖直向上抛出一物体，在运动过程中除受到重力外，还受到一大小恒定、方向始终与运动方向相反的空气阻力F阻的作用。距地面高度h在0至3 m以内时，物体上升、下落过程中动能Ek随h的变化如图所示。重力加速度取10m/s2 ， 该物体运动过程受到的空气阻力F阻为（ ）
A、0.5N B、1 N C、1.5 N D、2 N4. 如图所示，用长的轻质杆连着质量的小球在竖直平面内做圆周运动，。下列说法中正确的是（ ）
A、若小球恰能在竖直平面内做圆周运动，则其在最高点速率为 B、小球通过最高点时，小球受到杆的作用力不可能为零 C、小球通过最低点时受到轻杆的拉力 D、若小球以通过最高点，此时小球受到杆向下力的作用5. 如图所示，带正电小球静止在水平面上A点，BC为竖直放置的圆弧，圆弧与水平面相切，今在空间内加上水平向左的匀强电场。已知：电场力大小等于重力，均为10N，圆弧半径为0.3m，AB间距离为0.1m，不计空气和摩擦阻力。小球从静止出发到再次回到水平面的过程中（ ）
A、从B到C速率一直增加 B、动能最大值为1J C、距水平面的最大高度为0.1m D、再次回到水平面时与A点相距1.3m6. 质量为m=2kg的物体沿水平面向右做直线运动，t=0时刻受到一个水平向左的恒力F，如图甲所示，此后物体的v﹣t图象如图乙所示，取水平向右为正方向，g=10m/s2 ， 则（ ）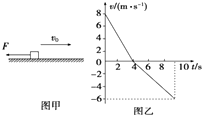
A、物体与水平面间的动摩擦因数为μ=0.5 B、10s末恒力F的功率为6W C、10s末物体恰好回到计时起点位置 D、10s内物体克服摩擦力做功34J7. 传送带是物料搬运系统机械化和自动化传送用具。如图，传送带靠静摩擦力把货箱从低处匀速送往高处，下列说法中正确的是（ ）
A、货箱与传送带间无相对滑动，静摩擦力不做功 B、货箱所受静摩擦力方向沿传送带向下 C、增大传送带斜面倾角，货箱受静摩擦力变大 D、货箱越重则越不容易相对传送带滑动8. 如图，倾斜的传送带以恒定的速率 沿顺时针方向匀速转动，一小物块从传送带上端A滑上传送带，滑上时速度大小为 、方向平行于传送带向下。若 ，物块与传送带间的动摩擦因数一定，不计空气阻力，则关于物块离开传送带时的位置和速率v，下列判断一定错误的是（ ）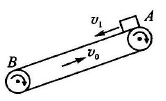
A、从上端A离开， B、从上端A离开， C、从下端B离开， D、从下端B离开，9. 如图所示，与水平面成角的传送带以的速度顺时针运行，质量为的小物块以初速度从底部滑上传送带，物块恰好能到达传送带顶端。已知物块与传送带间的动摩擦因数为 ， 取重力加速度。下列说法正确的是（ ）
A、传送带从底端到顶端的长度为1m B、物体在传送带上向上运动的时间为0.5s C、物块在传送带上留下的划痕长度为1.25m D、物体在传送带上向上运动过程中与传送带摩擦产生的热量为3.75J二、多项选择题
-
10. 如图所示，在竖直平面内有一“U”形槽，其底部BC是一段圆弧，两侧都与光滑斜槽相切，相切处B、C位于同一水平面上。一小物体从右侧斜槽上距BC所在水平面高度为2h的A处由静止开始下滑，经圆弧槽再滑上左侧斜槽，最高能到达距BC所在水平面高度为h的D处，接着小物体再向下滑回。若不考虑空气阻力，则（ ）
A、小物体恰好滑回到B处时速度为零 B、小物体第二次滑过圆弧槽时克服摩擦力做的功小于 C、小物体能滑回到B处之上，但最高点要比D处低 D、小物体最终一定会停止在圆弧槽的最低点11. 在大型物流货场，广泛的应用着传送带搬运货物。如图甲所示，与水平面倾斜的传送带以恒定速率运动，皮带始终是绷紧的，将m=1kg的货物放在传送带上的A处，经过1.2s到达传送带的B端。用速度传感器测得货物与传送带的速度v随时间t变化图像如图乙所示，已知重力加速度g=10m/s2。由v—t图可知（ ）
A、A，B两点的距离为2.4m B、货物与传送带的动摩擦因数为0.5 C、货物从A运动到B过程中，传送带对货物做功大小为12.8J D、货物从A运动到B过程中，货物与传送带摩擦产生的热量为4.8J12. 水平面上质量为m=10kg的物体受到的水平拉力F随位移s变化的规律如图所示，物体匀速运动一段时间后，拉力逐渐减小，当s=7.5m时拉力减为零，物体也恰好停下．取g=10m/s2 ， 下列结论正确的是（ ）
A、物体与水平面间的动摩擦因数为0.12 B、合外力对物体所做的功约为﹣40J C、物体匀速运动时的速度为2m/s D、物体运动的时间为0.4s13. 如图所示，某超市两辆相同的购物车质量均为m，相距L沿直线排列，静置于水平地面上。为节省收纳空间，工人猛推一下第一辆车并立即松手，第一辆车运动距离L后与第二辆车相碰并相互嵌套结为一体，两辆车一起运动了L距离后恰好停靠在墙边。若购物车运动时受到的摩擦力恒为车重的k倍，重力加速度为g，则（ ）
A、两购物车在整个过程中克服摩擦力做功之和为 B、两购物车碰撞后瞬间的速度大小为 C、两购物车碰撞时的能量损失为 D、工人给第一辆购物车的水平冲量大小为14. 如图，固定光滑长斜面倾角为37°，下端有一固定挡板。两小物块A、B放在斜面上，质量均为m，用与斜面平行的轻弹簧连接。一跨过轻小定滑轮的轻绳左端与B相连，右端与水平地面上的电动玩具小车相连。系统静止时，滑轮左侧轻绳与斜面平行，右侧轻绳竖直，长度为L且绳中无弹力，当小车缓慢向右运动上距离时A恰好不离开挡板．已知重力加速度大小为g，sin37o=0.6，cos37o=0.8。下列说法正确的是（ ）
A、弹簧的劲度系数为 B、当弹簧恢复原长时，物体B沿斜面向上移动了 C、若小车从图示位置以的速度向右匀速运动，小车位移大小为时；轻绳对B做的功为 D、当小车缓慢向右运动距离时，若轻绳突然断开，则此时B的加速度为1.2g，方向沿斜面向下三、非选择题
-
15. 如图甲所示，是一台质谱仪的简化结构模型。大量质量为 、电荷量为 的 粒子（即 核），从容器A下方飘入电势差为 的加速电场中，其初速度可视为0。若偏转电场不加电压， 粒子经加速后，将沿偏转电场的中轴线（图中虚线路径）出射后紧跟着马上垂直屏的方向射入一垂直纸面向外的匀强磁场中，经磁场偏转后击中屏。现在偏转电场两极间加上如图乙所示随时间变化的电压，其中 远大于粒子经过偏转电场的时间。偏转电场两板间宽度 ，两极板正对区域可视为匀强电场，正对区域以外的电场忽略不计。不计粒子所受重力和阻力，求：
(1)、 粒子出加速电场时速度 的大小；(2)、为使 粒子经偏转电场后能全部进入偏转磁场，偏转电场极板长度的取值范围；(3)、当偏转电场极板长度 时，若容器 中除了题干中已知的 粒子外，还存在另一种粒子氚核 ，为使两种粒子均能击中屏且击中屏的位置没有重叠，则偏转磁场的磁感应强度不能超过多少？16. 如图，一轻弹簧原长为2R，其一端固定在倾角为37°的固定直轨道AC的底端A处，另一端位于直轨道上B处，弹簧处于自然状态，直轨道与一半径为 的光滑圆弧轨道相切于C点，AC=7R，A、B、C、D均在同一竖直面内。质量为m的小物块P自C点由静止开始下滑，最低到达E点（未画出），随后P沿轨道被弹回，最高点到达F点，AF=4R，已知P与直轨道间的动摩擦因数 ，重力加速度大小为g。（取 ， ）
(1)、求P第一次运动到B点时速度的大小。(2)、求P运动到E点时弹簧的弹性势能。(3)、改变物块P的质量，将P推至E点，从静止开始释放。已知P自圆弧轨道的最高点D处水平飞出后，恰好通过G点。G点在C点左下方，与C点水平相距 、竖直相距R，求P运动到D点时速度的大小和改变后P的质量。17. 如图所示，在平面直角坐标系xOy中，第I象限存在沿y轴负方向的水平匀强电场，在x轴下侧平面内某处固定着一点电荷（设匀强电场与点电荷电场以x轴为界互不影响），一质量为m，电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ=60°角射入第IV象限，此后在点电荷作用下做匀速圆周运动，最后从y轴负半轴上的P点垂直于y轴射出，OP=3R．不计粒子重力，静电力常量为k，求：
(1)、M、N两点间的电势差UMN；(2)、固定x轴下侧平面内的点电荷电量Q；(3)、匀强电场的电场强度E大小．18. 如图所示，质量为m的工件，从高h的光滑曲面上由静止下滑，水平向右进入传送带，传送带以v0= 的速度匀速逆时针运动，传送带长L，工件与传送带之间的动摩擦因数μ= 。求：
(1)、工件离开传送带时的速度；(2)、工件在传送带上运动过程中产生的内能。19. 一质量为8.00×104 kg的太空飞船从其飞行轨道返回地面．飞船在离地面高度1.60×105 m处以7.5×103 m/s的速度进入大气层，逐渐减慢至速度为100m/s时下落到地面．取地面为重力势能零点，在飞船下落过程中，重力加速度可视为常量，大小取为9.8m/s2 ． （结果保留2位有效数字）
(1)、分别求出该飞船着地前瞬间的机械能和它进入大气层时的机械能；(2)、求飞船从离地面高度600m处至着地前瞬间的过程中克服阻力所做的功，已知飞船在该处的速度大小是其进入大气层时速度大小的2.0%．
20. 航空公司装卸货物时常因抛掷而造成物品损环，为解决这个问题，某同学设计了如图所示的缓冲转运装置。装置A上表面由光滑曲面和粗糙水平面组成，装置A紧靠飞机，转运车B紧靠A。已知包裹与装置A、转运车B水平上表面的动摩擦因数均为1=0.2，装置A与水平地面间的动摩擦因数2=0.1，最大静摩擦力大小等于滑动摩擦力，不计转运车B与水平地面间的摩擦。A、B的质量均为M=40kg，A、B水平上表面的长度均为L=4m。包裹可视为质点，将其由装置A的光滑曲面某高度h处静止释放，包裹与B的右挡板碰撞损失的机械能可忽略。重力加速度g取10m/s2。
(1)、要使包裹在装置A上运动时A不动，则包裹的质量最大不超过多少kg；(2)、若包裹质量m1=50kg，从高度h=0.2m处静止释放，包裹最终没有滑出装置A，求转运车B最终匀速运动时的动量；(3)、若包裹质量m2=10kg，为使包裹能停在转运车B上，则该包裹静止释放时的高度h应满足的条件。21. 如图所示，水平面右端放一质量m = 0.1kg小物块，使小物块以v0 = 4m/s的初速度向左运动，运动d = 1m后将弹簧压至最紧，反弹回出发点物块速度大小v1 = 2m/s。若水平面与一长L = 3m的水平传送带平滑连接，传送带以v2 = 10m/s的速度顺时针匀速转动。传送带右端又与一竖直平面内的光滑圆轨道的底端平滑连接，圆轨道半径R = 0.8m。当小物块进入圆轨道时会触发闭合装置将圆轨道封闭。（取g = 10 m/s2 ， sin53˚=0.8，cos53˚=0.6）求：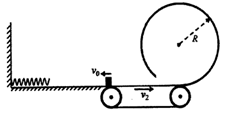
(1)、小物块与水平面间的动摩擦因数μ1；(2)、弹簧具有的最大弹性势能Ep；(3)、要使小物块进入竖直圆轨道后不脱离圆轨道，传送带与物体间的动摩擦因数μ2应满足的条件。22. 如图，水平传送带长为 ，且以 的恒定速率顺时针转动，光滑曲面与传送带的右端B点平滑连接，有一质量为 的物块（可视为质点）从距传送带高为 的A点由静止开始滑下。已知物块与传送带之间的动摩擦因数为 ，重力加速度 ，不计空气阻力。求：
(1)、物块在传送带上向左运动的最远距离；(2)、物块前两次经过B点的时间间隔；(3)、从开始运动到物块第n（ 且n为偶数）次经过B点时，物块与传送带间因摩擦而产生的热量。23. 如图所示，有一倾角为 的光滑斜面，其底端与水平传送带左端通过一小段光滑的圆弧在B点相连接，传送带沿顺时针方向匀速运行的速度大小为 ， 间距离为 。质量为m的滑块（视为质点），在大小为 的水平力作用下在斜面上高度为 处处于静止状态。现将水平力F撤去，当滑块滑到传送带右端C点时，恰好与传送带速度相同。重力加速度取 。求：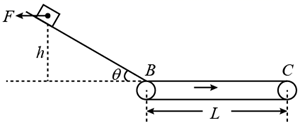
(1)、滑块的质量；(2)、滑块与传送带间的动摩擦因数；(3)、如果只将传送带调为逆时针匀速运行，速度大小调为 ，其他条件不变。仍把滑块从原位置由静止释放，求滑块在传送带上往返1次和往返n次，传送带摩擦力分别对滑块的冲量大小。