浙教版数学八年级下学期第一章二次根式 单元测试(培优版)
试卷更新日期:2024-02-26 类型:单元试卷
一、选择题
-
1. 若成立,则x的值可以是( )A、-2 B、0 C、2 D、32. 有下列式子: , , , , , (x>1).其中一定是二次根式的有( )A、2个 B、3个 C、4个 D、5个3. 式子 成立的条件是( )A、 ≥3 B、 ≤1 C、1≤ ≤3 D、1< ≤34. 若二次根式 有意义,且关于x的分式方程 +2= 有正数解,则符合条件的整数m的和是( )A、﹣7 B、﹣6 C、﹣5 D、﹣45. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、6. 化简二次根式 的结果为 ( )A、 B、 C、 D、7. 下列判断中,正确的是 ( )A、 B、若ab=0,则a=b=0 C、 D、可以表示面积为 a的正方形的边长8. 下列二次根式中,可以与 合并的是 ( )A、 B、 C、 D、9. 估计 的值在 ( )A、6和6.5之间 B、6.5和7之间 C、7 和7.5之间 D、7.5和8之间10. 如图,矩形内三个相邻的正方形的面积分别为 4,3,2,则图中阴影部分的面积为 ( )
 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11.
若
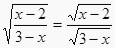 成立,则x满足12. 若x , y为实数,且 , 则 .13. 若整数x满足|x|≤3,则使为整数的x的值是 .14. 计算 .实数 的倒数是.15. 计算(1)、 .(2)、 .16. 计算( +1)2015( ﹣1)2014=
成立,则x满足12. 若x , y为实数,且 , 则 .13. 若整数x满足|x|≤3,则使为整数的x的值是 .14. 计算 .实数 的倒数是.15. 计算(1)、 .(2)、 .16. 计算( +1)2015( ﹣1)2014=
三、解答题
-
17. 求值(1)、先化简,再求值: ,其中 ;(2)、已知:a+ =1+ ,求 的值;(3)、已知实数m、n满足 ,求 的值.18. 先化简,再求值:已知y= ,求 的值.19. 先阅读下面的解题过程,然后再解答.形如 的化简,我们只要找到两个数a,b,使 , ,即 , ,那么便有: .
例如化简: .
解:首先把 化为 ,
这里 , ,
由于 , ,
所以 ,
所以 .
根据上述方法化简: .
20. 计算:(1)、(2)、已知 , , 求的值.21. 先阅读下列材料,再回答相应的问题若 与 同时成立,则x的值应是多少?
有下面的解题过程:
由于 与 都是算术平方根,故两者的被开方数 与 均为非负数.而 与 互为相反数,两个非负数互为相反数,只有一种情形,那便是 , 所以 .
问题:已知 ,求 的值.
22. 已知m为正整数,若是整数,则根据可知m有最小值3×7=21.设n为正整数,若是大于1的整数,求n的最小值和最大值