【提升卷】2024年北师大版数学八(下)2.6一元一次不等式组 同步练习
试卷更新日期:2024-02-25 类型:同步测试
一、选择题
-
1. 下列不等式组是一元一次不等式组的是( )A、
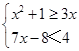 B、
B、  C、
C、 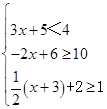 D、
D、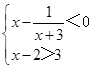 2. 把不等式组的解用数轴上的点表示出来,则其解构成的图形为( )A、射线 B、线段 C、直线 D、长方形3. 若数m使关于x的方程3x+m=x﹣5的解为负数,且使关于y的不等式组的解集为y>﹣2,则符合条件的所有整数m的和为( )A、﹣14 B、﹣9 C、﹣7 D、74. 若一个等腰三角形的周长为32,则该等腰三角形的腰长x的取值范围是( )A、0<x<32 B、0<x<16 C、8<x<16 D、8<x<325. 已知关于x的不等式组的整数解共有4个,则a的取值范围是( )A、﹣3<a≤﹣2 B、﹣3≤a<﹣2 C、﹣3<a<﹣2 D、a<﹣26. 如果关于的不等式组有且只有个奇数解,且关于的方程的解为非负整数,则符合条件的所有整数的积为( )A、 B、 C、 D、7. 已知关于x的不等式组 , 下列四个结论:
2. 把不等式组的解用数轴上的点表示出来,则其解构成的图形为( )A、射线 B、线段 C、直线 D、长方形3. 若数m使关于x的方程3x+m=x﹣5的解为负数,且使关于y的不等式组的解集为y>﹣2,则符合条件的所有整数m的和为( )A、﹣14 B、﹣9 C、﹣7 D、74. 若一个等腰三角形的周长为32,则该等腰三角形的腰长x的取值范围是( )A、0<x<32 B、0<x<16 C、8<x<16 D、8<x<325. 已知关于x的不等式组的整数解共有4个,则a的取值范围是( )A、﹣3<a≤﹣2 B、﹣3≤a<﹣2 C、﹣3<a<﹣2 D、a<﹣26. 如果关于的不等式组有且只有个奇数解,且关于的方程的解为非负整数,则符合条件的所有整数的积为( )A、 B、 C、 D、7. 已知关于x的不等式组 , 下列四个结论:①若它的解集是 , 则;②当 , 不等式组有解;③若它的整数解仅有3个,则a的取值范围是;④若它有解,则 .
其中正确的结论个数( )
A、1个 B、2个 C、3个 D、4个8. 如图是测量一颗玻璃球体积的过程:(1)将300ml的水倒进一个容量为500ml的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.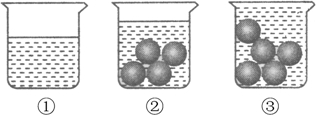
根据以上过程,推测这样一颗玻璃球的体积在( )
A、20cm3以上,30cm3以下 B、30cm3以上,40cm3以下 C、40cm3以上,50cm3以下 D、50cm3以上,60cm3以下二、填空题
-
9. 如图,数轴上表示的是关于x的一元一次不等式组的解集,则m的取值范围是 .
 10. 若实数m使关于x的不等式组有解且至多有2个整数解,且使关于y的方程的解为非负数,则满足条件的所有整数m的和为 .11. 一个运算程序,若需要经过2次运算才能输出结果,则x的取值范围为 .
10. 若实数m使关于x的不等式组有解且至多有2个整数解,且使关于y的方程的解为非负数,则满足条件的所有整数m的和为 .11. 一个运算程序,若需要经过2次运算才能输出结果,则x的取值范围为 . 12. 用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的 , 已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是acm,若铁钉总长度为6cm,则a的取值范围是 .
12. 用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的 , 已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是acm,若铁钉总长度为6cm,则a的取值范围是 .
三、解答题
-
13. 解下列不等式(组),并把其解在数轴上表示出来.(1)、 ≤1.(2)、14. 已知.(1)、求a+b的值;(2)、求7x+y200的值.15. 定义运算: , 已知 , .(1)、直接写出: , ;(2)、若关于的不等式组无解,求的取值范围;(3)、若的解集为 , 求不等式的解集.16. 某中学计划购买A型和型课桌凳共200套,经招标,购买一套型课桌凳比购买一套型课桌凳少用40元,且购买3套型和5套型课桌凳共需1640元.(1)、求购买一套型课桌凳和一套型课桌凳各需多少元?(2)、学校根据实际情况,要求购买这两种课桌凳的总费用不能超过40880元,并且购买型课桌凳的数量不能超过型课桌凳数量的 , 求该校本次购买型和型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.17. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②“包含”,其中不等式(组)①与不等式(组)②均有解.
例如:不等式被不等式“包含”.
(1)、下列不等式(组)中,能被不等式“包含”的是____.A、 B、 C、 D、(2)、若关于x的不等式被“包含”,若且 , 求M的最小值.(3)、已知 , , 且k为整数,关于x的不等式P: , Q: , 请分析是否存在k , 使得P和Q存在“包含”关系,且Q被P“包含”,若存在,请求出k的值,若不存在,请说明理由.