【培优卷】2024年北师大版数学八（下）2.6一元一次不等式组同步练习

试卷更新日期：2024-02-25 类型：同步测试

进入出卷网下载

一、选择题

1. 关于 $x$ 的不等式组 ${\begin{array}{l} x > 2 m \\ x \geq m - 3 \end{array}$ 的最小整数解为1，则 $m$ 的取值范围是（）

A、 $- 3 \leq m < 1$ B、 $0 \leq m < \frac{1}{2}$ C、 $3 < m \leq 4$ D、 $0 \leq m < \frac{1}{2}$ 或 $3 < m \leq 4$

查看试题解析
2. 若关于x的不等式组 ${\begin{cases} 6 x - 5 \geq m \\ \frac{x}{2} - \frac{x - 1}{3} < 1 \end{cases}$ 恰好有3个整数解，且关于y的方程 $\frac{y - 2}{3} = \frac{m - 2}{3} + 1$ 的解是非负数，则符合条件的所有整数m之和是（）

A、-6 B、-5 C、-3 D、-2

查看试题解析
3. 如果关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x - m}{3} \leq 1 \\ x - 4 > 3 (x - 2) \end{array}$ 的解集为 $x < 1$ ，且关于 $x$ 的分式方程 $\frac{2}{1 - x} + \frac{mx}{x - 1} = 3$ 有非负数解，则所有符合条件的整数 $m$ 的值之和是（）

A、-2 B、0 C、3 D、5

查看试题解析
4. 若整数a是使得关于x的不等式组 ${\begin{matrix} \frac{x - 1}{3} + 1 > \frac{x}{2} \\ 6 x - 5 \geq a \end{matrix}$ 有且仅有4个整数解，且使关于y的一元一次方程 $\frac{2 y + a}{5}$ ＝ $\frac{y - a}{3}$ ＋1的解满足y≤87.则所有满足条件的整数a的值之和为（）

A、﹣35 B、﹣30 C、﹣24 D、﹣17

查看试题解析
5. 有一根长40mm的金属棒，欲将其截成x根7mm长的小段和y根9mm长的小段，剩余部分作废料处理，若使废料最少，则正整数x，y应分别为（）

A、x=1，y=3 B、x=3，y=2 C、x=4，y=1 D、x=2，y=3

查看试题解析
6. 对非负实数n“四舍五入”到个位的值记为 $〈 x 〉$ ，即：当n为非负整数时，如果 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则 $〈 x 〉 = n$ ．反之，当n为非负整数时，如果 $〈 x 〉 = n$ 时，则 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，如 $〈 0 〉 = 〈 0.48 〉 = 0$ ， $〈 0.64 〉 = 〈 1.493 〉 = 1$ ， $〈 2 〉 = 2$ ， $〈 3.5 〉 = 〈 4.12 〉 = 4$ ，…若关于x的不等式组 ${\begin{array}{l} 2 x + 1 \geq - 3 \\ x - 〈 a 〉 < 0 \end{array}$ 的整数解恰有3个，则a的范围（）

A、1.5≤a＜2.5 B、0.5＜a≤1.5 C、1.5＜a≤2.5 D、0.5≤a＜1.5

查看试题解析
7. 运行程序如图所示，从“输入实数 x”到“结果是否＜18”为一次程序操作，若输入 x 后程序操作仅进行了三次就停止，那么 x 的取值范围是（）

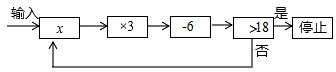A、 $x \geq \frac{32}{9}$ B、 $\frac{32}{9} \leq x \leq \frac{14}{3}$ C、 $\frac{32}{9} < x \leq \frac{14}{3}$ D、 $x \leq \frac{14}{3}$

查看试题解析
8. 检测游泳池的水质，要求三次检验的pH的平均值不小于7.2，且不大于7.8.前两次检验，pH的读数分别是7.4，7.9，那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x，由题意可得（）

A、7.2×3≤7.4+7.9+x≤7.8×3 B、7.2×3< 7.4+7.9+x≤7.8×3 C、7.2×3 >7.4+7.9+x>7.8×3 D、7.2×3< 7.4+7.9+x< 7.8×

查看试题解析

二、填空题

9. 邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．八（9）班有11位同学参加项目化学习知识竞赛，若每份答卷重12克，每个信封重4克，将这11份答卷分装在两个信封中寄出，所贴邮票的总金额最少是元．

查看试题解析
10. 若整数 $m$ 使得关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + y = 1 \\ 3 x - y = m \end{array}$ 的解为整数，且关于 $x$ 的不等式组 ${\begin{array}{l} 6 x + 1 \geq m \\ 3 x - 1 < 2 (x + 3) \end{array}$ 有且只有 $4$ 个整数解，则符合条件的所有 $m$ 的和为．

查看试题解析
11. 小明沿着某公园的环形跑道（周长大于 $1 k m$ ）按逆时针方向跑步，并用跑步软件记录运动轨迹，他从起点出发，每跑 $1 k m$ ，软件会在运动轨迹上标注出相应的里程数．前 $4 k m$ 的记录数据如图所示，当小明跑了2圈时，他的运动里程数 $3 k m$ （填“ $>$ ”“＝”或“ $<$ ”）；如果小明跑到 $10 k m$ 时恰好回到起点，那么此时小明总共跑的圈数为．

查看试题解析
12. 对于一个各数位上的数字均不为0的三位自然数N，若N能被它的各数位上的数字之和m整除，则称N是m的“整倍数”．例如：∵ $135 \div (1 + 3 + 5) = 135 \div 9 = 15$ ， ∴135是9的“整倍数”，又如∵ $524 \div (5 + 2 + 4) = 524 \div 11 = 47 ⋯ ⋯ 7$ ∴524不是11的“整倍数”．三位数A是12的“整倍数”，a，b，c分别是数A其中一个数位上的数字，且 $c < b < a$ ．在a，b，c中任选两个组成两位数，其中最大的两位数记为 $P (A)$ ，最小的两位数记为 $Q (A)$ ，若 $\frac{P (A) + Q (A)}{16}$ 为整数，求出满足条件的数A的最小值为．

查看试题解析
13. 对x ， y定义一种新的运算，规定 $F (x ， y) = {\begin{array}{l} x - 2 y (x \geq y) \\ y - x (x < y) \end{array} ，$ 例如 $F (2 ， 1) = 2 - 2 \times 1 = 0$

(1)、 $F (2 ， 3) =$ ；

(2)、若关于正数m的不等式组 ${\begin{array}{l} F (3 m ， m) > 1 \\ F (- 1 - 3 m ， - 2 m) \leq a \end{array}$ 恰好有2个整数解，则a的取值范围是．

查看试题解析

三、实践探究题

14. 我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[-2.5]＝-3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜-2.5＞＝-2．根据上述规定，解决下列问题：

(1)、[-4.5]＝，＜3.01＞＝；

(2)、若x为整数，且[x]+＜x＞＝2023，求x的值；

(3)、若x、y满足方程组 ${\begin{array}{l} 3 [x] + 2 < y > = 3 \\ 3 [x] - < y > = - 6 \end{array}$ ，求x、y的取值范围．

查看试题解析
15. 新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程 $x - 1 = 3$ 的解为 $x = 4$ ，而不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的解集为 $2 < x < 5$ ，不难发现 $x = 4$ 在 $2 < x < 5$ 的范围内，所以方程 $x - 1 = 3$ 是不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的“关联方程”．

(1)、在方程① $2 (x + 1) - x = - 3$ ；② $\frac{x + 1}{3} - 1 = x$ ；③ $2 x - 7 = 0$ 中，不等式组 ${\begin{array}{l} 2 x + 1 > x - 3 \\ 3 (x - 2) - x \leq 2 \end{array}$ 的“关联方程”是；（填序号）

(2)、关于x的方程 $2 x - k = 6$ 是不等式组 ${\begin{array}{l} \frac{x - 3}{2} \geq x \\ \frac{2 x + 5}{2} > \frac{1}{2} x \end{array}$ 的“关联方程”，求k的取值范围；

(3)、若关于x的方程 $\frac{x + 5}{2} - 3 m = 0$ 是关于x的不等式组 ${\begin{array}{l} \frac{x + 2 m}{2} > m \\ x - m \leq 2 m + 1 \end{array}$ 的“关联方程”，且此时不等式组有3个整数解，试求m的取值范围．

查看试题解析
16. 深化理解：
新定义：对非负实数 $x$ “四舍五入”到个位的值记为 $Z (x)$ ，即：当 $n$ 为非负整数时，如果 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则 $Z (x) = n$ ；
反之，当 $n$ 为非负整数时，如果 $Z (x) = n$ ，则 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ．
例如： $Z (0) = Z (0.48) = 0$ ， $Z (0.64) = Z (1.49) = 1$ ， $Z (2) = 2$ ， $Z (3.5) = Z (4.12) = 4$ ， $\dots$
试解决下列问题：

(1)、填空： $① Z (7.2) =$ ▲ ， $Z (π) =$ ▲ $(π$ 为圆周率 $)$ ， $Z (\sqrt{18}) =$ ▲ ；
$②$ 如果 $Z (x - 2) = 1$ ，求实数 $x$ 的取值范围；

(2)、若关于 $x$ 的不等式组 ${\begin{array}{l} \frac{2 x - 4}{3} \leq x - 1 \\ Z (a) - x > 0 \end{array}$ 的整数解恰有 $4$ 个，求 $a$ 的取值范围；

(3)、求满足 $Z (x) = \frac{5}{4} x$ 的所有非负实数 $x$ 的值．

查看试题解析
17. 在平面直角坐标系中，对于点 $P (x ， y)$ ，若点 $Q$ 的坐标为 $(a y + x ， a x + y)$ ，其中 $a$ 为常数，对称点 $Q$ 是点 $P$ 的“ $a$ 级关联点”，例如：点 $P (1 ， 4)$ 的“2级关联点” $Q (2 \times 4 + 1 ， 1 \times 2 + 4)$ ，即 $Q (9 ， 6)$ .

(1)、已知点 $A (2 ， - 1)$ 的：“3级关联点”为 $B$ ，求点 $B$ 的坐标；

(2)、已知点 $P (x ， y)$ 关于“2级关联点”为 $(0 ， 3)$ ，求 $P$ 的坐标；

(3)、点 $(2 m ， m - 1)$ 关于-4级关联点在第三象限，求 $m$ 的范围。

查看试题解析

【培优卷】2024年北师大版数学八（下）2.6一元一次不等式组 同步练习

一、选择题

二、填空题

三、实践探究题

【培优卷】2024年北师大版数学八（下）2.6一元一次不等式组同步练习