【提升卷】2024年北师大版数学八(下)2.5一元一次不等式与一次函数 同步练习
试卷更新日期:2024-02-25 类型:同步测试
一、选择题
-
1. 如图,在同一直角坐标系中,一次函数和的图象相交于点 , 则不等式的解集为( )
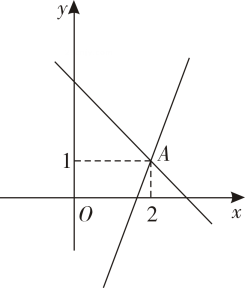 A、 B、 C、 D、2. 已知 , , 当时,总有 , 则a的值可以是( )A、 B、3 C、 D、23. 当时,对于x的每一个值,函数(k≠0)的值都小于函数的值,则k的取值范围是( )A、且 B、 C、 D、4. 已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A、
A、 B、 C、 D、2. 已知 , , 当时,总有 , 则a的值可以是( )A、 B、3 C、 D、23. 当时,对于x的每一个值,函数(k≠0)的值都小于函数的值,则k的取值范围是( )A、且 B、 C、 D、4. 已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A、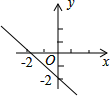 B、
B、 C、
C、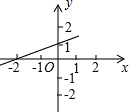 D、
D、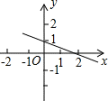 5. 如图,一次函数y=kx+b(k,b是常数,k≠0)与正比例函数y=mx(m是常数,m≠0)的图象相交于点M(1,2),下列判断中错误的是( )
5. 如图,一次函数y=kx+b(k,b是常数,k≠0)与正比例函数y=mx(m是常数,m≠0)的图象相交于点M(1,2),下列判断中错误的是( )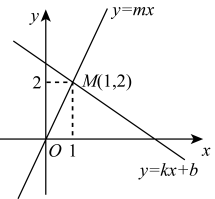 A、关于x的方程mx=kx+b的解是x=1 B、关于x的不等式mx≥kx+b的解是x>1 C、当x<0时,函数y=kx+b的值比函数y=mx的值大 D、关于x,y的方程组的解是6. 已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2 . 正确的个数是( )
A、关于x的方程mx=kx+b的解是x=1 B、关于x的不等式mx≥kx+b的解是x>1 C、当x<0时,函数y=kx+b的值比函数y=mx的值大 D、关于x,y的方程组的解是6. 已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2 . 正确的个数是( ) A、1 B、2 C、3 D、47. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为 , 下列结论:关于的方程的解为;对于直线 , 当时,;对于直线 , 当时,;方程组的解为 , 其中正确的是( )
A、1 B、2 C、3 D、47. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为 , 下列结论:关于的方程的解为;对于直线 , 当时,;对于直线 , 当时,;方程组的解为 , 其中正确的是( )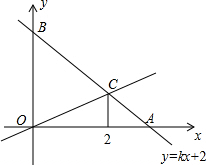 A、 B、 C、 D、8. 我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微”.请用这句话提到的数学思想方法解决下面的问题,已知函数 , 且关于 , 的二元一次方程有两组解,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、8. 我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微”.请用这句话提到的数学思想方法解决下面的问题,已知函数 , 且关于 , 的二元一次方程有两组解,则的取值范围是( )A、 B、 C、 D、二、填空题
-
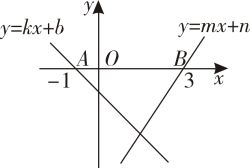
9. 如图,直线与直线分别与轴交于点、 , 则不等式的解集为
 10. 如图,在平面直角坐标系中,直线与直线相交于 , 则关于的不等式的解集是 .
10. 如图,在平面直角坐标系中,直线与直线相交于 , 则关于的不等式的解集是 .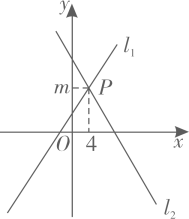 11. 一次函数(为常数,且)中的与的部分对应值如下表:
11. 一次函数(为常数,且)中的与的部分对应值如下表:2
0
下列结论中:①方程的解为;②若 , 则;③若的解为 , 则;④若关于的不等式的解集为 , 则 . 一定正确的是 .
12. 平面直角坐标系中,直线与相交于点 , 有下列结论: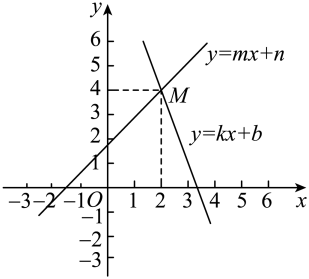
①关于x,y的方程组的解是;
②关于x的不等式的解集是;
③关于x的方程的解是;
④ .
其中,正确的是(填写序号).
三、解答题
-
13. 小函在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
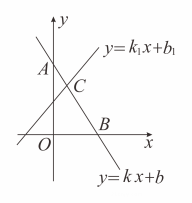
⑴一次函数的解析式就是一个二元一次方程;
⑵点B的横坐标是方程①的解;
⑶点C的坐标 中的x,y的值是方程组②的解.
⑴函数 的函数值y大于0时,自变量x的取值范围就是不等式③的解集;
⑵函数 的函数值y小于0时,自变量x的取值范围就是不等式④的解集.
(1)、请将以上方框中数字序号位置应有的内容填写在下面的相应位置:①;②;③;④;
(2)、如果点C的坐标为 ,那么不等式 的解集为 .14. 已知一次函数的图象经过点与 .(1)、求这个一次函数的解析式;(2)、判断点是否在这个一次函数的图象上;(3)、直接写出关于的一元一次不等式的解.15. 如图,在平面直角坐标系中,直线:分别与x轴、y轴交于点B、C,且与直线:交于点A.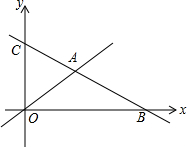 (1)、分别求出点A、B、C的坐标;(2)、直接写出关于x的不等式的解集;(3)、若D是线段OA上的点,且的面积为12,求直线CD的函数表达式.16. 某医药公司把一批药品运往外地,现有两种运输方式可供选择.
(1)、分别求出点A、B、C的坐标;(2)、直接写出关于x的不等式的解集;(3)、若D是线段OA上的点,且的面积为12,求直线CD的函数表达式.16. 某医药公司把一批药品运往外地,现有两种运输方式可供选择.方式一:使用快递公司的邮车运输,装卸收费400元,另外每千米再加收4元;
方式二:使用快递公司的火车运输,装卸收费820元,另外每千米再加收2元.
(1)、请你分别写出邮车、火车运输的总费用y1(元),y2(元)与路程x(km)之间的函数解析式;(2)、你认为选用哪种运输方式较好,为什么?