【培优卷】2024年北师大版数学八(下)2.5一元一次不等式与一次函数 同步练习
试卷更新日期:2024-02-25 类型:同步测试
一、选择题
-
1. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,2. 如图,直线 与 轴交于点 ,与直线 交于点 ,则关于 的不等式组 的解为( )
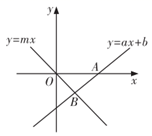 A、 B、 C、 D、3. 对于实数 , 定义符号其意义为:当时,;当时, . 例如: , 若关于的函数 , 则该函数的最大值是( )A、1 B、 C、 D、24. 如图,在平面直角坐标系中,若直线与直线相交于点 P,则下列结论错误的是( )
A、 B、 C、 D、3. 对于实数 , 定义符号其意义为:当时,;当时, . 例如: , 若关于的函数 , 则该函数的最大值是( )A、1 B、 C、 D、24. 如图,在平面直角坐标系中,若直线与直线相交于点 P,则下列结论错误的是( ) A、方程-x+a=bx-4的解是 x=1 B、不等式-x+a<-3和不等式bx-4>-3的解集相同 C、不等式组bx-4<-x+a<0的解集是-2<x<1 D、方程组的解是5. 函数 , 当 , 对应的取值范围为 , 则的取值范围为( )A、 B、 C、 D、6. 如图,已知直线 与 交点为P,根据图象有以下3个结论:① ;② ③ 是不等式 的解集.其中正确的个数是( )
A、方程-x+a=bx-4的解是 x=1 B、不等式-x+a<-3和不等式bx-4>-3的解集相同 C、不等式组bx-4<-x+a<0的解集是-2<x<1 D、方程组的解是5. 函数 , 当 , 对应的取值范围为 , 则的取值范围为( )A、 B、 C、 D、6. 如图,已知直线 与 交点为P,根据图象有以下3个结论:① ;② ③ 是不等式 的解集.其中正确的个数是( ) A、0 B、1 C、2 D、37. 如图,一次函数y1=ax+b(a,b是常数)的图象与y轴、x轴分别交于点A(0,3)、点B,正比例函数y2=x的图象与一次函数y1的图象交于点P(m,1),有下列结论:
A、0 B、1 C、2 D、37. 如图,一次函数y1=ax+b(a,b是常数)的图象与y轴、x轴分别交于点A(0,3)、点B,正比例函数y2=x的图象与一次函数y1的图象交于点P(m,1),有下列结论:
①一次函数y1的图象与y轴交点的纵坐标为3;
②方程ax+b=0的解为x=4.5;
③不等式ax+b<0的解集为x>4.5,其中正确的有( )A、3个 B、2个 C、1个 D、0个8. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是 .
其中结论正确的个数是( )
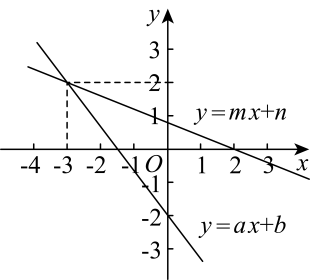 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,函数和的图象相交于点 , 则关于 x 的不等式 的解集为 .
 10. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 .
10. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 . 11. 若直线经过点 , 经过点 , 且与关于轴对称,则关于的不等式的解集为 .12. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .13. 一次函数与的图象如图所示,则下列结论:①;②a<0,b>0;③当时,;④不等式的解集是 , 其中正确的结论有.
11. 若直线经过点 , 经过点 , 且与关于轴对称,则关于的不等式的解集为 .12. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .13. 一次函数与的图象如图所示,则下列结论:①;②a<0,b>0;③当时,;④不等式的解集是 , 其中正确的结论有.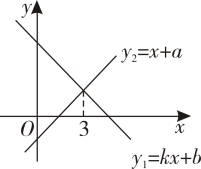 14. 已知直线过点﹒则以下结论:①;②若当时, , 则;③方程组的解为;④若直线向右平移2个单位后过点 , 且不等式的解集为 , 则 , 其中正确的有 . (请填写序号)
14. 已知直线过点﹒则以下结论:①;②若当时, , 则;③方程组的解为;④若直线向右平移2个单位后过点 , 且不等式的解集为 , 则 , 其中正确的有 . (请填写序号)三、解答题
-
15. 已知一次函数的图象交x轴和y轴于点B和D;另一个一次函数的图象交x轴和y轴于点C和E,且两个函数的图象交于点(1)、当a,b为何值时,和的图象重合;(2)、当 , 且在时,则成立,求b的取值范围;(3)、当的面积为时,求线段的长.
四、实践探究题
-
16. 某班“数学兴趣小组”根据学习一次函数的经验,对函数y=|x-2|的图像和性质进行了研究.探究过程如下,请补充完整.(1)、自变量x的取值范围是全体实数.下表是y与x的几组对应值:
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
5
4
m
2
1
0
1
2
3
…
其中,m=;
(2)、如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,并画出了函数图象的一部分,请画出该函数图象的另一部分; (3)、观察函数图象发现,该函数图象的最低点坐标是;
(3)、观察函数图象发现,该函数图象的最低点坐标是;当x<2时,y随x的增大而减小;当x≥2时,y随x的增大而;
(4)、进一步探究,①不等式|x-2|≥1.5的解集是;
②若关于x的方程|x-2|=kx (k≠0)只有一个解,则k的取值范围是 .
17. 综合与探究如图,在平面直角坐标系中,直线与轴,轴分别交于点 , , 与直线交于点 .
 (1)、求点的坐标;(2)、根据图像,直接写出不等式的解集;(3)、若点为坐标平面内任意一点,试探究:是否存在点 , 使是以为腰的等腰直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求点的坐标;(2)、根据图像,直接写出不等式的解集;(3)、若点为坐标平面内任意一点,试探究:是否存在点 , 使是以为腰的等腰直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
-