【基础卷】2024年北师大版数学八(下)2.5一元一次不等式与一次函数 同步练习
试卷更新日期:2024-02-25 类型:同步测试
一、选择题
-
1. 一次函数的图象如图所示,当时,的取值范围是( )
 A、 B、 C、 D、2. 如图,直线y=kx+b(k、b是常数,且k≠0)与x轴交于点A(-3,0),与y轴交于点B(0,2),则不等式kx+b<0的解( )
A、 B、 C、 D、2. 如图,直线y=kx+b(k、b是常数,且k≠0)与x轴交于点A(-3,0),与y轴交于点B(0,2),则不等式kx+b<0的解( ) A、x>-3 B、x<-3 C、x>2 D、x<23. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
A、x>-3 B、x<-3 C、x>2 D、x<23. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( ) A、x< B、x<3 C、x> D、x>34. 如图,直线:与直线:交于点 , 则不等式的解集是( )
A、x< B、x<3 C、x> D、x>34. 如图,直线:与直线:交于点 , 则不等式的解集是( ) A、 B、 C、 D、5. 如图,已知直线与相交于点 , 则关于的不等式的解集在数轴上表示正确的是( )
A、 B、 C、 D、5. 如图,已知直线与相交于点 , 则关于的不等式的解集在数轴上表示正确的是( )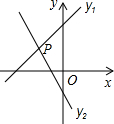 A、
A、 B、
B、 C、
C、 D、
D、 6. 已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )
6. 已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )x
-2
-1
0
1
2
3
y
4
3
2
1
0
-1
A、x<0 B、x>0 C、x<2 D、x>27. 已知直线y=3x+3﹣a与x轴的交点在A(1,0),B(4,0)之间(包括A , B两点),则a的取值范围( )A、6<a<15 B、1≤a≤4 C、﹣1≤a≤2 D、6≤a≤158. 已知一次函数的图象过点 , 则不等式的解集是( )A、 B、 C、 D、二、填空题
-
9. 观察图中的函数图象,则关于x的不等式ax-bx>c的解为.
 10. 如图,已知函数y=﹣x+b与函数y=kx+7的图象交于点P(﹣2,3),则关于x的不等式﹣x+b≤kx+7的解集是 .
10. 如图,已知函数y=﹣x+b与函数y=kx+7的图象交于点P(﹣2,3),则关于x的不等式﹣x+b≤kx+7的解集是 . 11. 在一次函数中,当时,的取值范围是.12. 直线y=kx+2与直线y=2x+b(k,b为常数)交于点(1,0),则关于x的不等式kx+b>0的解集为 .
11. 在一次函数中,当时,的取值范围是.12. 直线y=kx+2与直线y=2x+b(k,b为常数)交于点(1,0),则关于x的不等式kx+b>0的解集为 .三、解答题
-
13. 小明在学习了一元一次不等式和一次函数后,把相关知识归纳整理如下:
一次函数与不等式的关系:
知识点1:函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式 ① 的解;
知识点2:函数y=kx+b的丽数值y小于0时,自变量x的取值范围就是不等式 ② 的解.
(1)、请你根据以上内容在下面序号后写出相应的式子.①;②.
(2)、如图,若点B的坐标为(2,5),求不等式kx+b≥k1x+b1的解. 14. 已知 y1=2x+4,y2=5x+10,当x取哪些值时,y1<y2?
14. 已知 y1=2x+4,y2=5x+10,当x取哪些值时,y1<y2?