2024年浙教版数学八年级下册3.1平均数课后培优练

试卷更新日期：2024-02-25 类型：同步测试

进入出卷网下载

一、选择题

1. 下表是某校 $12$ 名男子足球队的年龄分布：
年龄（岁）
$13$
$14$
$15$
$16$
频数
$1$
$2$
$5$
$4$
该校男子足球队队员的平均年龄为（）

A、 $13$ B、 $14$ C、 $15$ D、 $16$

查看试题解析
2. 某校对学生一学期的各学科学业的总平均分是按如图所示的雨形图信息要求进行计算的已知该校八年级一班李明同学这个学期的数学成绩如下表：

李明

平时作业

期中考试

期末考试

90

85

88

则李明这个学期数学的总平均例为（）

A、87.5 B、87.6 C、87.7 D、87.8

查看试题解析
3. 双十一期间，某超市以优惠价销售 $A ， B ， C ， D ， E$ 坚果五种礼盒，它们的单价分别为 $90$ 元、 $80$ 元， $70$ 元， $60$ 元， $50$ 元，当天销售情况如图所示，则当天销售坚果礼盒的平均售价为（）

A、 $75$ 元 B、 $70$ 元 C、 $66.5$ 元 D、 $65$ 元

查看试题解析
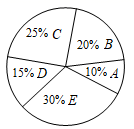4. 已知：x₁ ， x₂ ， x₃...x₁₀的平均数是a,x₁₁ ， x₁₂ ， x₁₃...x₅₀的平均数是b,则x₁ ， x₂ ， x₃...x₅₀的平均数是（）

A、a＋b B、 $\frac{a + b}{2}$ C、 $\frac{10 a + 50 b}{60}$ D、 $\frac{10 a + 40 b}{50}$

查看试题解析
5. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85、90、95，则该选手的综合成绩为（）

A、92 B、88 C、90 D、95

查看试题解析
6. 某快递公司快递员张山某周投放快递物品件数为：有4天是30件，有2天是35件，有1天是41件，这周里张山日平均投递物品件数为（）

A、35.3件 B、35件 C、33件 D、30件

查看试题解析
7. 8名学生的平均成绩是x，如果另外2名学生每人得84分，那么整个组的平均成绩是（）

A、 B、 C、 D、

查看试题解析
8. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析

二、填空题

9. 某果农将直径从65 mm至85 mm的苹果每相差5 mm分为1个等级，共分为A，B，C，D四个等级，它们每箱的价格依次是20元，30元，40元，50元某天这四个等级苹果销售数量的百分比如图所示，则这天销售的苹果每箱平均价格为.

查看试题解析
10. 水果店里有A，B，C三种不同大小型号的杨梅出售，售价分别为a元/斤，b元/斤，c元/斤.某顾客购买了5斤A型号，7斤B型号，5斤C型号的杨梅，则该顾客购买这些杨梅的平均价格为元/斤

查看试题解析
11. 已知一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ ， $x_{5}$ 的平均数是3，则数据 $2 x_{1} - 1$ ， $2 x_{2} - 1$ ， $2 x_{3} - 1$ ， $2 x_{4} - 1$ ， $2 x_{5} - 1$ 的平均数是．

查看试题解析
12. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析

三、综合题

13. 某公司招聘人才，对应聘者分别进行阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的成绩如表：（单位：分）

项目

选手

阅读能力

思维能力

表达能力

甲

94

87

74

乙

96

82

80

(1)、甲、乙两人“三项测试”的平均成绩分别为分、分；

(2)、根据实际需要，公司将阅读能力、思维能力和表达能力三项测试成绩按3：5：2的比确定每位应聘者的成绩，请你计算甲、乙两人的平均成绩，从他们的成绩看，应该录取谁？

查看试题解析
14. 某班欲从甲、乙两名同学中推出一名同学，参加学校组织的数学素质测试竞赛，首先在班内对甲、乙两名同学进行了数与代数、图形与几何、统计与概率、综合与实践的测试，他们的各项成绩（百分制）如下表所示：
学生
数与代数
图形与几何
统计与概率
综合与实践
甲
85
89
92
94
乙
94
92
85
80

(1)、如果各项成绩同等重要，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？

(2)、若数与代数、图形与几何、统计与概率、综合与实践的成绩按 $4 ： 3 ： 2 ： 1$ 的比确定，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？

查看试题解析
15. 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如右表．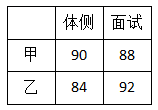

(1)、当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？

(2)、当体侧成绩权重为 $a$ ，面试和体侧各有权重，并且权总和为10，请问当 $a$ 取什么范围，乙成绩比甲高？

查看试题解析

学生	数与代数	图形与几何	统计与概率	综合与实践
甲	85	89	92	94
乙	94	92	85	80

年龄（岁）	$13$	$14$	$15$	$16$
频数	$1$	$2$	$5$	$4$

李明	平时作业	期中考试	期末考试
李明	90	85	88