【北师大版·数学】2024年中考二轮复习之反比例函数的综合题
试卷更新日期:2024-02-24 类型:二轮复习
一、选择题
-
1. 在反比例函数(k为常数)的图象上有三个点(-3,y1),(-1,y2), , 则函数值y1 , y2 , y3的大小关系为( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y22. 如图,在平面直角坐标系中,的顶点C , A分别在x轴,y轴上, , , 且斜边轴.若反比例函数的图象恰好经过的中点D , 则k的值为( )
 A、 B、 C、 D、3. 如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
A、 B、 C、 D、3. 如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( ) A、x>﹣2 B、﹣2<x<0或x>1 C、x>1 D、x<﹣2或0<x<14. 如图,B、C两点分别在函数和 y= - (x<0)的图象上,线段BC⊥y轴,点A在x轴上,则△ABC的面积为( )
A、x>﹣2 B、﹣2<x<0或x>1 C、x>1 D、x<﹣2或0<x<14. 如图,B、C两点分别在函数和 y= - (x<0)的图象上,线段BC⊥y轴,点A在x轴上,则△ABC的面积为( ) A、9 B、6 C、3 D、45. 如图,直线轴于点 , 且与反比例函数及的图象分别交于点 , , 连接 , , 已知的值为 , 则的面积为( )
A、9 B、6 C、3 D、45. 如图,直线轴于点 , 且与反比例函数及的图象分别交于点 , , 连接 , , 已知的值为 , 则的面积为( ) A、 B、 C、 D、6. 已知P是反比例函数y= (x>0) 图象上一点,A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,则点P的坐标为( )
A、 B、 C、 D、6. 已知P是反比例函数y= (x>0) 图象上一点,A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,则点P的坐标为( ) A、(3,4) B、(2,6) C、(6,2) D、(4,3)7. 安乡子龙汽车站与常德市柳叶湖汽车站相距约 , 则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间小时与行驶速度千米时之间的函数图象大致是( )A、
A、(3,4) B、(2,6) C、(6,2) D、(4,3)7. 安乡子龙汽车站与常德市柳叶湖汽车站相距约 , 则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间小时与行驶速度千米时之间的函数图象大致是( )A、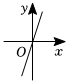 B、
B、 C、
C、 D、
D、 8. 如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO , ∠AOB=90°,则k的值为( )
8. 如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO , ∠AOB=90°,则k的值为( ) A、1 B、2 C、1.5 D、0.259. 已知点 , , 都在反比例函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、10. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、1 B、2 C、1.5 D、0.259. 已知点 , , 都在反比例函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、10. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则二、填空题
-
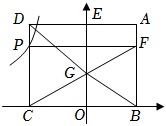
11. 如图,矩形中,点 , 在轴上,交轴于点 , 点在上, , 连接交轴于点 , 过点作轴交于点 , 点在函数的图象上.若的面积为 , 则的值为 ;的面积与的面积差为 .
 12. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.13. 如图点A,B在反比例函数y=上,连接AB分别交x,y轴于点D、点C,将△DOA沿OA翻折点D刚好落在y轴上的点F处,AF与x轴交于点E,已知 , S△DOB=2,则k= .
12. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.13. 如图点A,B在反比例函数y=上,连接AB分别交x,y轴于点D、点C,将△DOA沿OA翻折点D刚好落在y轴上的点F处,AF与x轴交于点E,已知 , S△DOB=2,则k= . 14. 如果一个正比例函数的图象与反比例函数的图象交于 , 两点,那么的值为 .15. 如图,直线与轴,轴分别交于 , 两点,且与反比例函数的图象交于点 , 若 , 则 .
14. 如果一个正比例函数的图象与反比例函数的图象交于 , 两点,那么的值为 .15. 如图,直线与轴,轴分别交于 , 两点,且与反比例函数的图象交于点 , 若 , 则 .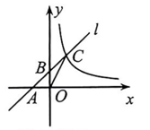
三、解答题
-
16. 如图,正比例函数与反比例函数的图象交于A,两点,点C在x轴负半轴上, .
 (1)、 , , 点C的坐标为 .(2)、点P在x轴上,若以B,O,P为顶点的三角形与相似,求点P的坐标.17. 如图所示,已知 , 是一次函数图象与反比例函数图象的两个交点.
(1)、 , , 点C的坐标为 .(2)、点P在x轴上,若以B,O,P为顶点的三角形与相似,求点P的坐标.17. 如图所示,已知 , 是一次函数图象与反比例函数图象的两个交点.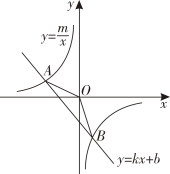 (1)、求反比例函数和一次函数的表达式;(2)、观察图象,当取何值时, .18. 笑笑同学通过学习数学和物理知识,知道了电磁波的波长(单位:m)会随着电磁波的频率f(单位:)的变化而变化.已知波长与频率f是反比例函数关系,下面是它们的部分对应值:
(1)、求反比例函数和一次函数的表达式;(2)、观察图象,当取何值时, .18. 笑笑同学通过学习数学和物理知识,知道了电磁波的波长(单位:m)会随着电磁波的频率f(单位:)的变化而变化.已知波长与频率f是反比例函数关系,下面是它们的部分对应值:频率f()
10
15
50
波长(m)
30
20
6
(1)、求波长关于频率f的函数解析式.(2)、当时,求此电磁波的波长 .19. 如图,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(﹣ ,2),B(n,﹣1). (1)、求直线与双曲线的解析式.
(1)、求直线与双曲线的解析式.
(2)、点P在x轴上,如果S△ABP=3,求点P的坐标.
四、实践探究题
-
20. 视力表中蕴含着很多数学知识,如:每个“
 ”形图都是正方形结构,同一行的“
”形图都是正方形结构,同一行的“ ”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表. 素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值 , 测得对应行的“
 ”形图边长 , 在平面直角坐标系中描点如图1.
”形图边长 , 在平面直角坐标系中描点如图1.探究1检测距离为5米时,归纳与的关系式,并求视力值1.2所对应行的“
 ”形图边长.
”形图边长.
素材2图2为视网膜成像示意图,在检测视力时,眼晴能看清最小“
 ”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).
”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).探究2当时,属于正常视力,根据函数增减性写出对应的分辦视角的范围.
素材3如图3,当确定时,在处用边长为的号“
 ”测得的视力与在处用边长为的Ⅱ号“
”测得的视力与在处用边长为的Ⅱ号“ ”测得的视力相同.
”测得的视力相同.探究3若检测距离为3米,求视力值1.2所对应行的“
 ”形图边长.
”形图边长.