备考2024年浙江中考数学一轮复习专题16.2二次函数 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 已知二次函数 , 下列说法正确的是( )A、点在该函数的图象上 B、当且时, C、该函数的图象与x轴一定有交点 D、当时,该函数图象的对称轴一定在直线的左侧2. 已知点 A(a,2)、B(b,2)、C(c,7)都在抛物线 上,点A在点B左侧,下列选项正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2 , 那么球弹起后又回到地面所花的时间t(秒)是( )A、5 B、10 C、1 D、24. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或45. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为6. 已知二次函数是常数,的图象上有和两点.若点A,B都在直线的上方,且 , 则的取值范围是( )A、 B、 C、 D、7. 在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(﹣3,﹣6) B、(1,﹣4) C、(1,﹣6) D、(﹣3,﹣4)8. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
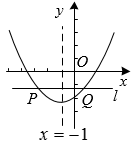 A、 B、若实数 ,则 C、 D、当 时,9. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:
A、 B、若实数 ,则 C、 D、当 时,9. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为 .
其中,正确结论的个数是( )
 A、0 B、1 C、2 D、310. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
A、0 B、1 C、2 D、310. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=.
 12. 如图,抛物线与x轴相交于点、点 , 与y轴相交于点C , 点D在抛物线上,当轴时, .
12. 如图,抛物线与x轴相交于点、点 , 与y轴相交于点C , 点D在抛物线上,当轴时, . 13. 如图,在直线:上方的双曲线上有一个动点 , 过点作轴的垂线,交直线于点 , 连接 , , 则面积的最大值是 .
13. 如图,在直线:上方的双曲线上有一个动点 , 过点作轴的垂线,交直线于点 , 连接 , , 则面积的最大值是 .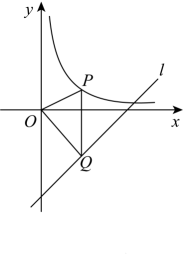 14. 如图,二次函数的图象与正比例函数的图象相交于A , B两点,已知点A的横坐标为 , 点B的横坐标为2,二次函数图象的对称轴是直线 . 下列结论:①;②;③关于x的方程的两根为 , ;④ . 其中正确的是 . (只填写序号)
14. 如图,二次函数的图象与正比例函数的图象相交于A , B两点,已知点A的横坐标为 , 点B的横坐标为2,二次函数图象的对称轴是直线 . 下列结论:①;②;③关于x的方程的两根为 , ;④ . 其中正确的是 . (只填写序号)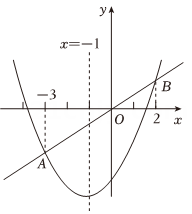 15. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是 .
15. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是 . 16. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
16. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
三、解答题(共7题,共54分)
-
17. 在二次函数中,(1)、若它的图象过点 , 则t的值为多少?(2)、当时,y的最小值为 , 求出t的值:(3)、如果都在这个二次函数的图象上,且 , 求m的取值范围。18. 已知二次函数(为常数).(1)、该函数图象与轴交于两点,若点坐标为 ,
①则的值是 ▲ , 点的坐标是 ▲ ;
②当时,借助图像,求自变量的取值范围;
(2)、对于一切实数 , 若函数值总成立,求的取值范围(用含的式子表示);(3)、当时(其中为实数,),自变量的取值范围是 , 求和的值以及的取值范围.19. 某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)(30≤x<60)存在一次函数关系,部分数据如表所示:销售价格x(元/千克)
50
40
日销售量y(千克)
100
200
(1)、试求出y关于x的函数表达式.(2)、设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?20. 某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元件设第个生产周期设备的售价为万元件,售价与之间的函数解析式是 , 其中是正整数当时,;当时, .(1)、求 , 的值;(2)、设第个生产周期生产并销售完设备的数量为件,且与满足关系式 .当时,工厂第几个生产周期获得的利润最大?最大的利润是多少万元?
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
21. 如图,二次函数的图象与轴相交于点和点 , 交轴于点 . (1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).22. 某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程与时间的近似函数图象.启航阶段的函数表达式为;途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程与时间的函数表达式为.
(1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).22. 某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程与时间的近似函数图象.启航阶段的函数表达式为;途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程与时间的函数表达式为.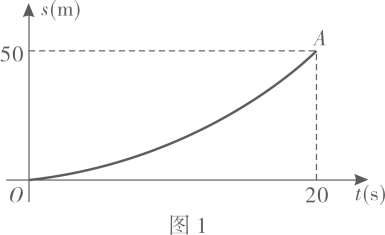
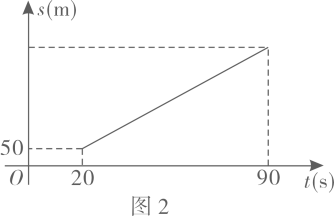 (1)、求出启航阶段关于的函数表达式(写出自变量的取值范围).(2)、已知途中阶段龙舟速度为.
(1)、求出启航阶段关于的函数表达式(写出自变量的取值范围).(2)、已知途中阶段龙舟速度为.①当时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,视为达标.请说明该龙舟队能否达标.
(3)、冲刺阶段,加速期龙舟用时将速度从提高到 , 之后保持匀速划行至终点.求该龙舟以完成训练所需时间(精确到).23. 如图1,在平面直角坐标系xOy中,二次函数y=x2-4x+c的图象与y轴的交点坐标为(0,5),图象的顶点为M . 矩形ABCD的顶点D与原点O重合,顶点A , C分别在x轴,t轴上,顶点B的坐标为(1,5).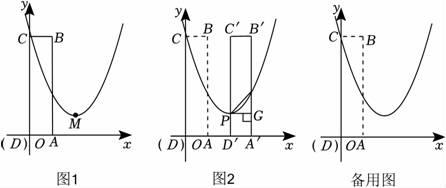 (1)、求c的值及顶点M的坐标.(2)、如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2-4x+c的图象交于点P , Q , 连结PQ , 过点P作PG⊥A′B′于点G .
(1)、求c的值及顶点M的坐标.(2)、如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2-4x+c的图象交于点P , Q , 连结PQ , 过点P作PG⊥A′B′于点G .①当t=2时,求QG的长;
②当点G与点Q不重合时,是否存在这样的t , 使得△PGQ的面积为1?若存在,求出此时t的值;若不存在,请说明理由.
四、实践探究题(共2题,共18分)
-
24. 已知关于的函数.(1)、若 , 函数的图象经过点和点 , 求该函数的表达式和最小值;(2)、若 , , 时,函数的图象与轴有交点,求的取值范围.(3)、阅读下面材料:
设 , 函数图象与轴有两个不同的交点 , , 若 , 两点均在原点左侧,探究系数 , , 应满足的条件,根据函数图象,思考以下三个方面:
①因为函数的图象与轴有两个不同的交点,所以;
②因为 , 两点在原点左侧,所以对应图象上的点在轴上方,即;
③上述两个条件还不能确保 , 两点均在原点左侧,我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置:即需.
综上所述,系数 , , 应满足的条件可归纳为:
请根据上面阅读材料,类比解决下面问题:
若函数的图象在直线的右侧与轴有且只有一个交点,求的取值范围.
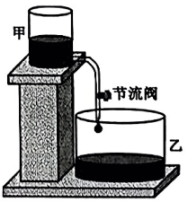
25. 【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】
综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如下表:
流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务1 分别计算表中每隔10min水面高度观察值的变化量.
【建立模型】
小组讨论发现:“ , ”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2 利用时,;时,这两组数据求水面高度h与流水时间t的函数解析式.
【反思优化】
经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差.小组决定优化函数解析式,减少偏差.通过查阅资料后知道:t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和 , 记为w;w越小,偏差越小.
任务3 ⑴计算任务2得到的函数解析式的w值.
⑵请确定经过的一次函数解析式,使得w的值最小.
【设计刻度】
得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4 请你简要写出时间刻度的设计方案.