备考2024年浙江中考数学一轮复习专题16.1二次函数 基础夯实
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 下列函数不属于二次函数的是( )A、 B、 C、 D、2. 若A( , ),B( , ),C( , )为二次函数的图象上的三点,则的大小关系是( )A、 B、 C、 D、3. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、
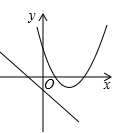 B、
B、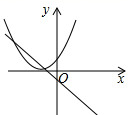 C、
C、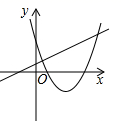 D、
D、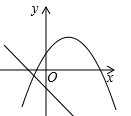 4. 在平面直角坐标系中,二次函数y=(m为常数)的图象经过点(0,6),其对称轴在y轴左侧,则该二次函数有( )A、最大值5 B、最大值 C、最小值5 D、最小值5. 在研究二次函数时,下面是某小组列出的部分和的对应值:
4. 在平面直角坐标系中,二次函数y=(m为常数)的图象经过点(0,6),其对称轴在y轴左侧,则该二次函数有( )A、最大值5 B、最大值 C、最小值5 D、最小值5. 在研究二次函数时,下面是某小组列出的部分和的对应值:…
1
…
…
8
8
…
根据表格可知,下列说法中错误的是( )
A、该二次函数图象的对称轴是直线 B、关于的方程的解是 , C、的最大值是8 D、的值是6. 若抛物线的函数表达式为y=(x-2)²-9,有下列结论:①当x=2时,y取得最小值-9;
②若点(3,y₁),(4,y₂)在其图象上,则y₂>y₁;
③将其函数图象向左平移3个单位,再向上平移4个单位所得抛物线的函数表达式为④函数图象与x轴有两个交点,且两交点的距离为6.其中正确的是( )
A、②③④ B、①②④ C、①③ D、①②③④7. 如图,抛物线 , 与轴正半轴交于两点, 与轴负半轴交于点 .①;
②;
③若点的坐标为 , 且 , 则;
④若抛物线的对称轴是直线 , 为任意实数;
则 .
上述结论中,正确的个数是( )
 A、0个 B、1个 C、2个 D、3个8. 已知 ,且 ,其中 , ,则 的取值范围( )A、 B、 C、 D、9. 约定:若函数图象上至少存在不同的两点关于原点对称,则把该函数称为“黄金函数”,其图象上关于原点对称的两点叫做一对“黄金点”.若点 , 是关于的“黄金函数”上的一对“黄金点”,且该函数的对称轴始终位于直线的右侧;则下列结论:①;②:③;④ , 正确的是( )A、①②③ B、①②④ C、②③④ D、①③④10. 九年级一班的同学计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A、0个 B、1个 C、2个 D、3个8. 已知 ,且 ,其中 , ,则 的取值范围( )A、 B、 C、 D、9. 约定:若函数图象上至少存在不同的两点关于原点对称,则把该函数称为“黄金函数”,其图象上关于原点对称的两点叫做一对“黄金点”.若点 , 是关于的“黄金函数”上的一对“黄金点”,且该函数的对称轴始终位于直线的右侧;则下列结论:①;②:③;④ , 正确的是( )A、①②③ B、①②④ C、②③④ D、①③④10. 九年级一班的同学计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )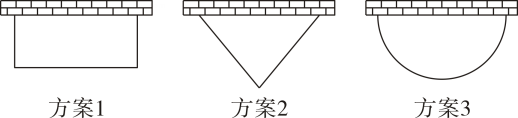 A、方案1 B、方案2 C、方案3 D、三种方案使得菜园面积一样大
A、方案1 B、方案2 C、方案3 D、三种方案使得菜园面积一样大二、填空题(每题3分,共18分)
-
11. 请写出一个开口向上,并且与y轴交于点(0,1)的抛物线的解析式。
12. 将二次函数用配方法化成的形式为y= .13. 将抛物线y=x2向下平移3个单位,再向右平移2个单位后,所得抛物线的解析式为.14. 关于的二次函数 , 在时有最大值6,则 .15. 已知在二次函数y=ax2+bx+c中,函数值y与自变量x的部分对应值如表:x
…
-1
0
1
2
3
…
y
…
8
3
0
-1
0
…
则满足方程ax2+bx+c=0的解是 .
16. 抛物线与轴相交于不同两点、 , 若存在整数及整数 , 使得和同时成立,则 .三、综合题(共7题,共54分)
-
17. 已知二次函数y=x2﹣2x﹣3
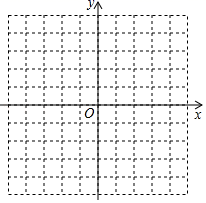 (1)、求函数图象的顶点坐标,与坐标轴的交点坐标,并画出函数的大致图象;(2)、根据图象直接回答:当y<0时,求x的取值范围;当y>﹣3时,求x的取值范围.18. 毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)、求函数图象的顶点坐标,与坐标轴的交点坐标,并画出函数的大致图象;(2)、根据图象直接回答:当y<0时,求x的取值范围;当y>﹣3时,求x的取值范围.18. 毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.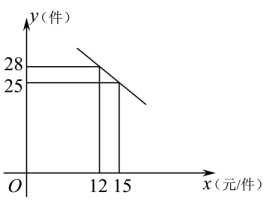 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?19.
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?19.如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为m.
 (1)、求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(1)、求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)、一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?20. 某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:
销售单价x(元/千克)
---
20
22.5
25
37.5
40
…
销售量y(千克)
---
30
27.5
25
12.5
10
…
(1)、根据表中的数据在如图的坐标系中描点(x,y),并用平滑的线连结这些点,请用所学知识求出y关于x的函数表达式.(2)、设该超市每天销售这种商品的利润为w(元)(不计其他成本).①求出w关于x的函数表达式,并求出获得最大利润时,销售单价为多少.
②超市本着“尽量让顾客享受实惠”的销售原则,求w=240元时的销售单价.
21. 如图,小静和小林在玩沙包游戏,沙包(看成点)抛出后,在空中的运动轨迹可看作抛物线的一部分,小静和小林分别站在点O和点A处,测得距离为 , 若以点O为原点,所在直线为x轴,建立如图所示的平面直角坐标系,小林在距离地面的B处将沙包抛出,其运动轨迹为抛物线:的一部分,小静恰在点处接住,然后跳起将沙包回传,其运动轨迹为抛物线:的一部分.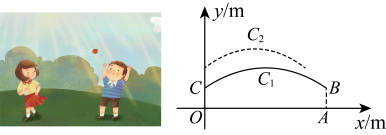 (1)、抛物线的最高点坐标为;(2)、求a , c的值;(3)、小林在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,若小林成功接到小静的回传沙包,则n的整数值可为 .22. 如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C.
(1)、抛物线的最高点坐标为;(2)、求a , c的值;(3)、小林在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,若小林成功接到小静的回传沙包,则n的整数值可为 .22. 如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C. (1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.
(1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)、在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.23. 如图,二次函数的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).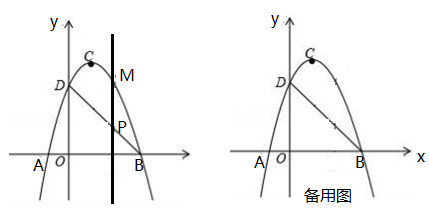 (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作X轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为 , 若存在求出点Q的坐标;若不存在请说明理由.
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作X轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为 , 若存在求出点Q的坐标;若不存在请说明理由.四、实践探究题(共2题,共18分)
-
24. 【定义】在平面直角坐标系中,有一条直线 , 对于任意一个函数图象,把该图象在直线上的点以及直线右边的部分向上平移(为正整数)个单位长度,再把直线左边的部分向下平移个单位长度,得到一个新的函数图象,则这个新函数叫做原函数关于直线的“移函数”,例如:函数关于直线的2移函数为.
根据以上信息,解答下列问题:
(1)、已知点在函数()关于直线的“3移函数”图象上,求的值;(2)、若二次函数关于直线的“移函数”与轴有三个公共点,设是这三个点的横坐标之和,是否存在一个正整数 , 使得的值为整数?若存在,求出的值;若不存在,请说明理由.25. 根据以下素材,探究完成任务素材1 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD= 12cm,
此时面汤最大深度EG= 6cm,
素材2 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止.

问题解决 任务1 确定碗体形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式。
任务2 拟定设计方案1 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。
任务3 拟定设计方案2 如图3,当碗停止倾斜时,求此时碗中液面宽度CH。