备考2024年浙江中考数学一轮复习专题15.2反比例函数 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 如果100N的压力F作用于物体上,产生的压强p要大于1000Pa,则下列关于物体受力面积S(m2)的说法正确的是( )A、S小于0.1m2 B、S大于0.1m2 C、S小于10m2 D、S大于10m22. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、3. 若正比例函数y=2kx与反比例函数(k≠0)的图象交于点A(m,1),则k的值是( )A、或 B、或 C、 D、4. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
 B、
B、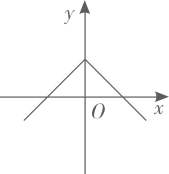 C、
C、 D、
D、 5. 已知点(-2,a),(2,b),(3,c)在函数 的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a6. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和7.
5. 已知点(-2,a),(2,b),(3,c)在函数 的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a6. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和7.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
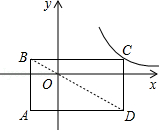 A、1 B、﹣5 C、4 D、1或﹣58. 如图,一次函数的图像与反比例函数的图像相交于两点,点的横坐标为1,点的横坐标为 , 当时,的取值范围是( )
A、1 B、﹣5 C、4 D、1或﹣58. 如图,一次函数的图像与反比例函数的图像相交于两点,点的横坐标为1,点的横坐标为 , 当时,的取值范围是( ) A、或 B、或 C、或 D、或9. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点 . 若点坐标为 , 则的值是( ).
A、或 B、或 C、或 D、或9. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点 . 若点坐标为 , 则的值是( ).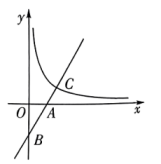 A、 B、 C、 D、10. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<1
A、 B、 C、 D、10. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<1二、填空题(每题4分, 共24分)
-
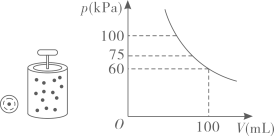
11. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对气缸壁所产生的压强与气缸内气体的体积成反比例,关于的函数图象如图所示.若压强由加压到 , 则气体体积压缩了.
 12. 如图,已知动点A在函数 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
12. 如图,已知动点A在函数 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .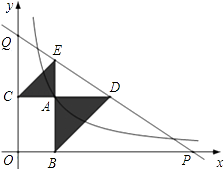 13. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
13. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
 14. 如图,点和在反比例函数的图象上,其中过点作轴于点 , 则的面积为;若的面积为 , 则 .
14. 如图,点和在反比例函数的图象上,其中过点作轴于点 , 则的面积为;若的面积为 , 则 . 15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是.
15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是. 16. 如图,点A,B分别在函数图象的两支上(A在第一象限),连接AB交x轴于点C.点D,E在函数图象上,轴,轴,连接 . 若 , 的面积为9,四边形的面积为14,则的值为 , a的值为 .
16. 如图,点A,B分别在函数图象的两支上(A在第一象限),连接AB交x轴于点C.点D,E在函数图象上,轴,轴,连接 . 若 , 的面积为9,四边形的面积为14,则的值为 , a的值为 .
三、解答题(共6题,共42分)
-
17. 笑笑同学通过学习数学和物理知识,知道了电磁波的波长(单位:m)会随着电磁波的频率f(单位:)的变化而变化.已知波长与频率f是反比例函数关系,下面是它们的部分对应值:
频率f()
10
15
50
波长(m)
30
20
6
(1)、求波长关于频率f的函数解析式.(2)、当时,求此电磁波的波长 .18. 如图,正比例函数与反比例函数的图象交于A,两点,点C在x轴负半轴上, . (1)、 , , 点C的坐标为 .(2)、点P在x轴上,若以B,O,P为顶点的三角形与相似,求点P的坐标.19. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, .
(1)、 , , 点C的坐标为 .(2)、点P在x轴上,若以B,O,P为顶点的三角形与相似,求点P的坐标.19. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, . (1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .20. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
(1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .20. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 . (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.21. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.21. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),①求函数y1 , y2的表达式:
②当2<x<3时,比较y1与y2的大小(直接写出结果).
(2)、若点C(2,n)在函数y1的图象上,点C先向下平移2个单位,再向左平移4个单位,得点D,点D恰好落在函数y1的图象上,求n的值,22. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B.
 (1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
(1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;
②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
四、实践探究题(共2题,共24分)
-
23. 规定:若函数的图像与函数的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.(1)、下列三个函数①;②;③ , 其中与二次函数互为“兄弟函数”的是(填写序号);(2)、若函数与互为“兄弟函数”,是其中一个“兄弟点”的横坐标.
①求实数a的值;
②直接写出另外两个“兄弟点”的横坐标是 ▲ 、 ▲ ;
(3)、若函数(m为常数)与互为“兄弟函数”,三个“兄弟点”的横坐标分别为、、 , 且 , 求的取值范围.24. 视力表中蕴含着很多数学知识,如:每个“ ”形图都是正方形结构,同一行的“
”形图都是正方形结构,同一行的“ ”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表. 素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值 , 测得对应行的“
 ”形图边长 , 在平面直角坐标系中描点如图1.
”形图边长 , 在平面直角坐标系中描点如图1.探究1检测距离为5米时,归纳与的关系式,并求视力值1.2所对应行的“
 ”形图边长.
”形图边长.
素材2图2为视网膜成像示意图,在检测视力时,眼晴能看清最小“
 ”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).
”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).探究2当时,属于正常视力,根据函数增减性写出对应的分辦视角的范围.
素材3如图3,当确定时,在处用边长为的号“
 ”测得的视力与在处用边长为的Ⅱ号“
”测得的视力与在处用边长为的Ⅱ号“ ”测得的视力相同.
”测得的视力相同.探究3若检测距离为3米,求视力值1.2所对应行的“
 ”形图边长.
”形图边长.