备考2024年浙江中考数学一轮复习专题14.2一次函数 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、 B、2 C、 D、12. 已知点在下列某一函数图象上,且那么这个函数是( )A、 B、 C、 D、3. 若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于( )A、-1 B、0 C、3 D、44. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
 B、
B、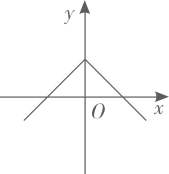 C、
C、 D、
D、 5. 已知二次函数是常数,的图象上有和两点.若点A,B都在直线的上方,且 , 则的取值范围是( )A、 B、 C、 D、6. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限7. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
5. 已知二次函数是常数,的图象上有和两点.若点A,B都在直线的上方,且 , 则的取值范围是( )A、 B、 C、 D、6. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限7. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( ) A、M1 B、M2 C、M3 D、M48. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、M1 B、M2 C、M3 D、M48. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )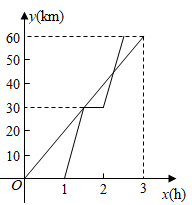 A、15km B、16km C、44km D、45km9. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、410. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
A、15km B、16km C、44km D、45km9. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、410. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )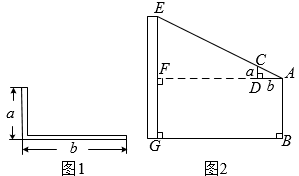 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分, 共24分)
-
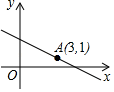
11. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是12. 如图,直线 经过点 ,当 时, 的取值范围为 .
 13. 关于x的一次函数 , 若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是.14. 如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+a<bx-4的解集是.
13. 关于x的一次函数 , 若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是.14. 如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+a<bx-4的解集是.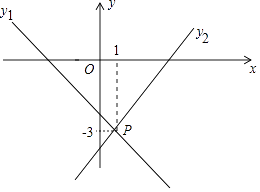 15. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .
15. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .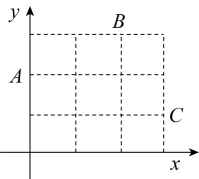 16. 如图,在平面直角坐标系中,直线l:与x轴交于点 , 以为边作正方形点在y轴上,延长交直线l于点 , 以为边作正方形 , 点在y轴上,以同样的方式依次作正方形 , …,正方形 , 则点的横坐标是 .
16. 如图,在平面直角坐标系中,直线l:与x轴交于点 , 以为边作正方形点在y轴上,延长交直线l于点 , 以为边作正方形 , 点在y轴上,以同样的方式依次作正方形 , …,正方形 , 则点的横坐标是 .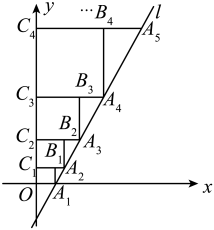
三、解答题(共6题,共45分)
-
17. 一次函数的图象与x轴交于点A , 且经过点.
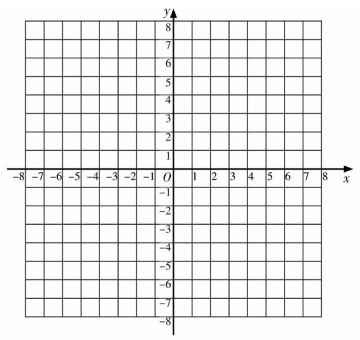 (1)、求点A和点B的坐标;(2)、直接在图6的平面直角坐标系中画出一次函数的图象;(3)、点P在x轴的正半轴上,若是以为腰的等腰三角形,请直接写出所有符合条件的P点坐标.18. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点.
(1)、求点A和点B的坐标;(2)、直接在图6的平面直角坐标系中画出一次函数的图象;(3)、点P在x轴的正半轴上,若是以为腰的等腰三角形,请直接写出所有符合条件的P点坐标.18. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点. (1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.19. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象.
(1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.19. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象. (1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.20. 一次函数y=kx+b(k≠0)的图象经过点A(2,﹣6),且与反比例函数y=﹣ 的图象交于点B(a,4)(1)、求一次函数的解析式;(2)、将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= 的图象相交,求使y1<y2成立的x的取值范围.21. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
(1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.20. 一次函数y=kx+b(k≠0)的图象经过点A(2,﹣6),且与反比例函数y=﹣ 的图象交于点B(a,4)(1)、求一次函数的解析式;(2)、将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= 的图象相交,求使y1<y2成立的x的取值范围.21. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
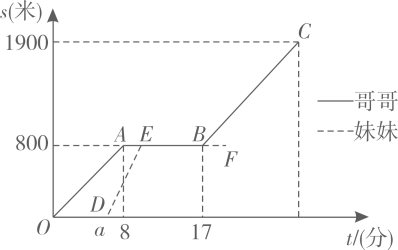 (1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
(1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值;
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.22. 一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).x
0
0.5
1
1.5
2
y
1
1.5
2
2.5
3
为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择: ( ),y=ax2+bx+c ( ), ( ).
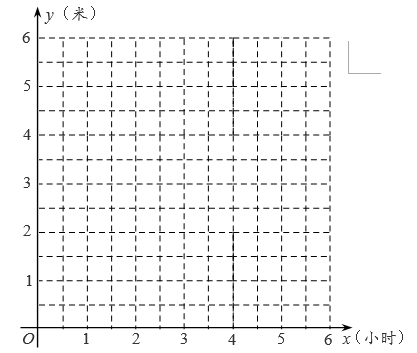 (1)、在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)、当水位高度达到5米时,求进水用时x.
(1)、在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)、当水位高度达到5米时,求进水用时x.四、实践探究题(共2题,共21分)
-
23. 综合与实践
如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为 .

【问题提出】
小组同学提出这样一个问题:若 , 能否围出矩形地块?
(1)、【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为 , 为 . 由矩形地块面积为 , 得到 , 满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为 , 得到 , 满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 , 因此,木栏总长为时,能围出矩形地块,分别为: , ;或m , m .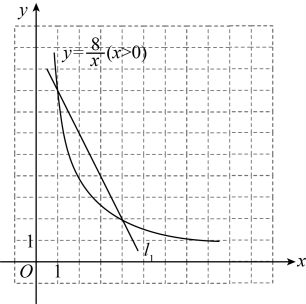
根据小颖的分析思路,完成上面的填空.(2)、【类比探究】若 , 能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)、【问题延伸】当木栏总长为时,小颖建立了一次函数 . 发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)、【拓展应用】小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于 , 请直接写出的取值范围.
24. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点 是函数 的图象的“等值点”.(1)、分别判断函数 的图象上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、设函数 的图象的“等值点”分别为点A,B,过点B作 轴,垂足为C.当 的面积为3时,求b的值;(3)、若函数 的图象记为 ,将其沿直线 翻折后的图象记为 .当 两部分组成的图象上恰有2个“等值点”时,直接写出m的取值范围.