备考2024年浙江中考数学一轮复习专题14.1一次函数 基础夯实
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 下列关于的函数中,是正比例函数的是( )A、 B、 C、 D、2. 一次函数 和正比例函数 在同一直角坐标系中的函数图象可能是( )A、
 B、
B、 C、
C、 D、
D、 3. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)4. 某品牌的自行车链条每节长为 , 每两节链条相连部分重叠的圆的直径为 , 按照这种连接方式,节链条总长度为 , 则与的关系式是( )
3. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)4. 某品牌的自行车链条每节长为 , 每两节链条相连部分重叠的圆的直径为 , 按照这种连接方式,节链条总长度为 , 则与的关系式是( ) A、 B、 C、 D、5. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、
A、 B、 C、 D、5. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、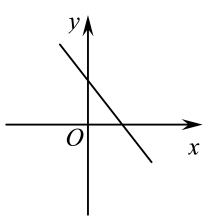 B、
B、 C、
C、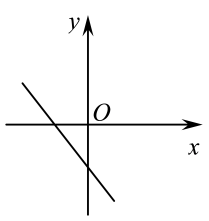 D、
D、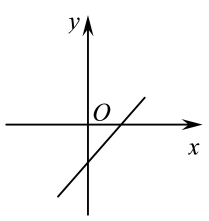 6. 若一次函数 的图像过第一、三、四象限,则函数 ( )A、有最大值 B、有最大值 C、有最小值 D、有最小值7. 对于函数 , 下列结论正确的是( )A、函数图象与y轴的交点坐标是 B、函数图象经过点 C、y随x的增大而减小 D、此函数图象经过第一、二、三象限8. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返的速度大小不变,两车离甲地的距离y(km)与慢车行驶时间t(h)的函数关系如图所示,则两车先后两次相遇的间隔时间是( )
6. 若一次函数 的图像过第一、三、四象限,则函数 ( )A、有最大值 B、有最大值 C、有最小值 D、有最小值7. 对于函数 , 下列结论正确的是( )A、函数图象与y轴的交点坐标是 B、函数图象经过点 C、y随x的增大而减小 D、此函数图象经过第一、二、三象限8. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返的速度大小不变,两车离甲地的距离y(km)与慢车行驶时间t(h)的函数关系如图所示,则两车先后两次相遇的间隔时间是( )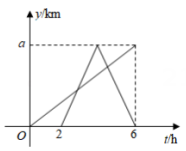 A、h B、h C、h D、h9. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( )
A、h B、h C、h D、h9. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( ) A、1 B、2 C、4 D、610. 在平面直角坐标系中,点 在直线 上,过点 作 轴于点 ,作等腰直角三角形 ( 与原点O重合),再以 为腰作等腰直角三角形 ,以 为腰作等腰直角三角形 ,…按照这样的规律进行下去,那么 的坐标为( )
A、1 B、2 C、4 D、610. 在平面直角坐标系中,点 在直线 上,过点 作 轴于点 ,作等腰直角三角形 ( 与原点O重合),再以 为腰作等腰直角三角形 ,以 为腰作等腰直角三角形 ,…按照这样的规律进行下去,那么 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分, 共24分)
-
11. 已知 是一次函数,则m=.12. 在平面直角坐标系xOy中,若点(1,y1),(4,y2)在一次函数y=kx+b(k>0)的图象上,则y1y2(填“>”,“=”或“<”).13. 函数和的图象相交于点 , 则方程的解为 .
 14. 在平面直角坐标系中,将直线y=2+4沿向右平移2个单位长后,得到新直线的函数关系式为.15. 已知关于x、y的二元一次方程组的解是 , 则一次函数和的图像交点坐标为 .16. 已知平面内有两条直线 l1: , l2:交于点 , 与x轴分别交于 , 两点,落在内部(不含边界),则的取值范围是 .
14. 在平面直角坐标系中,将直线y=2+4沿向右平移2个单位长后,得到新直线的函数关系式为.15. 已知关于x、y的二元一次方程组的解是 , 则一次函数和的图像交点坐标为 .16. 已知平面内有两条直线 l1: , l2:交于点 , 与x轴分别交于 , 两点,落在内部(不含边界),则的取值范围是 .三、解答题(共6题,共46分)
-
17. 已知y是x的一次函数,当x=2时,y=3,当x=﹣2时,y=﹣5,求:
 (1)、这个一次函数的解析式;(2)、画出该函数的图象.18. 在平面直角坐标系中,一次函数的图象与函数的图象平行,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于x的每一个值,函数的值大于一次函数的值,直接写出m的取值范围.19. 如图,在平面直角坐标系中,直线y=x+b分别与x轴、轴交于点A,B,且点A的坐标为(4,0),四边形ABCD是正方形.
(1)、这个一次函数的解析式;(2)、画出该函数的图象.18. 在平面直角坐标系中,一次函数的图象与函数的图象平行,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于x的每一个值,函数的值大于一次函数的值,直接写出m的取值范围.19. 如图,在平面直角坐标系中,直线y=x+b分别与x轴、轴交于点A,B,且点A的坐标为(4,0),四边形ABCD是正方形. (1)、填空:b=.(2)、点M是线段AB上的一个动点(点A,B除外),试探索在x轴上方是否存在另一个点N,使得以O,B,M,N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标(提示:两直线垂直,斜率乘积为-1)20. 用张甲种木板(规格:)和张乙种木板(规格:)制作 , 两种顶部无盖的木盒若干个, , 两种木盒尺寸(单位:)如图.为了降低成本,制作木盒时,甲种木板不裁开,除棱以外其他地方不拼接,且甲、乙两种木板刚好全部用完.
(1)、填空:b=.(2)、点M是线段AB上的一个动点(点A,B除外),试探索在x轴上方是否存在另一个点N,使得以O,B,M,N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标(提示:两直线垂直,斜率乘积为-1)20. 用张甲种木板(规格:)和张乙种木板(规格:)制作 , 两种顶部无盖的木盒若干个, , 两种木盒尺寸(单位:)如图.为了降低成本,制作木盒时,甲种木板不裁开,除棱以外其他地方不拼接,且甲、乙两种木板刚好全部用完. (1)、求可制作 , 两种木盒各多少个?(2)、已知种木盒的销售单价是种木盒的两倍,且两种木盒的销售单价之和不低于元而不超过元,设种木盒的销售单价为元.当制作这批木盒的成本为元时,为使这批木盒的销售利润最大,两种木盒的销售单价应分别定为多少元?销售这批木盒的最大利润为多少元?21. 已知甲、乙两地相距480km,一辆出租车从甲地出发往返于甲、乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题:
(1)、求可制作 , 两种木盒各多少个?(2)、已知种木盒的销售单价是种木盒的两倍,且两种木盒的销售单价之和不低于元而不超过元,设种木盒的销售单价为元.当制作这批木盒的成本为元时,为使这批木盒的销售利润最大,两种木盒的销售单价应分别定为多少元?销售这批木盒的最大利润为多少元?21. 已知甲、乙两地相距480km,一辆出租车从甲地出发往返于甲、乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题: (1)、图中的值是.(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数表达式.(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距12km.22. 某电商平台甲、乙、丙三个直播间的促销活动如下表所示:
(1)、图中的值是.(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离y(km)与行驶时间x(h)之间的函数表达式.(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距12km.22. 某电商平台甲、乙、丙三个直播间的促销活动如下表所示:直播间 活动 甲 全场六折 乙 “满 100 送 100 ” (如: 购买 190 元商品,赠 100 元购物券;购买 200 元商品, 赠200 元购物券) 丙 “满 100 堿 50” (如 : 购买 190 元商品,只需付 140 元; 购买 200 元商品,只需付100 元) 请根据上述信息,解答下列问题:
(1)、甲、乙两个直播间同时出售一款标价为380元的破壁机和一款标价为300多元的空气炸锅,小明妈妈想买这两件厨房用品.小明通过计算发现在甲直播间同时购买这两件商品与在乙直播间先买破壁机再买空气作锅所花的钱是相同的,求空气炸锅的标价.(2)、小明研究了丙直播间的活动方案,发现实际售价y(元)可以看成标价x(元)的函数,并绘制了如图所示的部分函数图象.请写出当100≤x<200时,y关于x的函数表达式,并在图中画出这个函数的图象. (3)、在甲、丙两个直播间标价均为x元(0<x<200)的商品,当x的取值范围是多少时,到甲直播间购买更合算?
(3)、在甲、丙两个直播间标价均为x元(0<x<200)的商品,当x的取值范围是多少时,到甲直播间购买更合算?四、实践探究题(共2题,共20分)
-
23. 综合与实践.
【问题情境】“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图(a)所示的液体漏壶,该漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.

【实验观察】下表是实验记录的圆柱容器液面高度与时间的数据:
时间 1 2 3 4 5 6圆柱容器液面高度 6 10 14 18 22 (1)、【探索发现】请你根据表中的数据在图(b)中描点、连线,用所学过的一次函数的知识确定与之间的函数表达式;
(2)、【结论应用】如果本次实验记录的开始时间是上午 , 那么当圆柱容器液面高度达到时是几点?
24. 根据以下素材,探索完成任务确定文具套餐售价
素材1
某书店销售一款文具套装,当每套文具售价为30元时,月销售量为200套,经市场调查表明,每套文具售价每降价1元,则月销售量增加20套.设每套文具的售价为x元(x为正整数),月销售量为y套. 素材2
该文具套装的成本是10元/套.
素材3
为促进公益,在售价不低于进价且每套文具获利不高于95%的前提下,该书店决定,每月捐赠400元给慈善机构. 问题解决:
(1)、任务1:分析变量分析求y关于x的函数表达式.
(2)、任务2:计算月利润当售价为多少时,月利润W获得最大?最大利润是多少?
(3)、任务3:确定合理售价为了保证捐款后月利润不低于3040元,文具套装的售价可以取哪些数值.