备考2024年浙江中考数学一轮复习专题13.2函数初步 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共36分)
-
1. 下列图象中,表示y是x的函数的个数有( )
 A、1个 B、2个 C、3个 D、4个2. 函数y与自变量x的部分对应值如表所示,则下列函数表达式中,符合表中对应关系的可能是( )
A、1个 B、2个 C、3个 D、4个2. 函数y与自变量x的部分对应值如表所示,则下列函数表达式中,符合表中对应关系的可能是( )x
1
2
4
y
4
2
1
A、 B、 C、 D、3. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A、x与y都是变量,且x是自变量,y是因变量 B、弹簧不挂重物时的长度为0cm C、物体质量每增加1kg,弹簧长度y增加0.5 cm D、所挂物体质量为7kg时,弹簧长度为13.5cm4. 已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…
A、y=2x B、y=x﹣1 C、y= D、y=x25. 生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( ) A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系6. 如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能符合题意反映容器中水的高度( )与时间( )之间对应关系的大致图象是( ).
A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系6. 如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能符合题意反映容器中水的高度( )与时间( )之间对应关系的大致图象是( ). A、
A、 B、
B、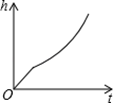 C、
C、 D、
D、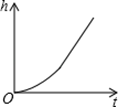 7. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( )
7. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( ) A、
A、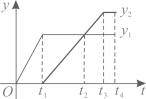 B、
B、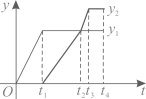 C、
C、 D、
D、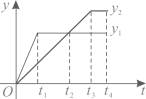 8. 如图1,在中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中长与运动时间t(单位:s)的关系如图2,则的长为( )
8. 如图1,在中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中长与运动时间t(单位:s)的关系如图2,则的长为( )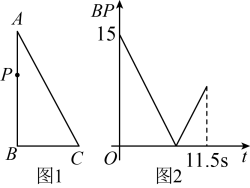 A、 B、 C、17 D、9. 中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系:折线表示轿车离西昌距离与时间之间的函数关系,则以下结论错误的是( )
A、 B、 C、17 D、9. 中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系:折线表示轿车离西昌距离与时间之间的函数关系,则以下结论错误的是( ) A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km10. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )
A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km10. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )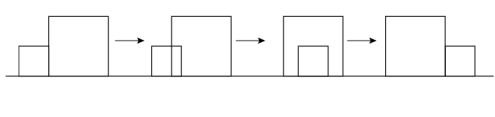 A、
A、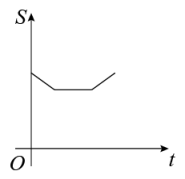 B、
B、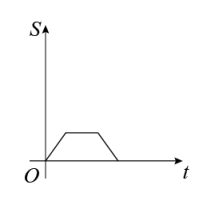 C、
C、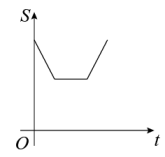 D、
D、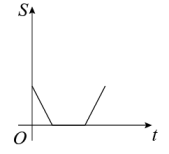 11. 折返跑是一种跑步的形式.如图,在一定距离的两个标志物①、②之间,从①开始,沿直线跑至②处,用手碰到②后立即转身沿直线跑至①处,用手碰到①后继续转身跑至②处,循环进行,全程无需绕过标志物.小华练习了一次的折返跑,用时在整个过程中,他的速度大小v()随时间t()变化的图像可能是( )
11. 折返跑是一种跑步的形式.如图,在一定距离的两个标志物①、②之间,从①开始,沿直线跑至②处,用手碰到②后立即转身沿直线跑至①处,用手碰到①后继续转身跑至②处,循环进行,全程无需绕过标志物.小华练习了一次的折返跑,用时在整个过程中,他的速度大小v()随时间t()变化的图像可能是( ) A、
A、 B、
B、 C、
C、 D、
D、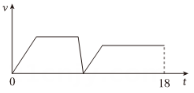 12. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣1
12. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣1二、填空题(每题3分,共18分)
-
13. 函数y=的自变量x的取值范围是 .
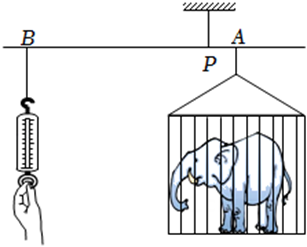
14. 请写出一个函数的表达式,使得它的图象经过点: .15. 拖拉机工作时,油箱中的余油量 (升)与工作时间 (时)的关系式为 .当 时, , 从关系式可知道这台拖拉机最多可工作小时.16. 某动物园利用杠杆原理称象;如图,在点P处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点A、B处,当钢梁保持水平时,弹簧秤读数为k(N),若铁笼固定不动,移动弹簧秤使BP扩大到原来的n(n>1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含n,k的代数式表示)
 17. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .
17. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .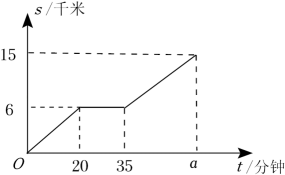 18. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
18. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
三、解答题(共7题,共66分)
-
19. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)、根据上表可知,该车油箱的大小为升,每小时耗油升;(2)、请求出两个变量之间的关系式(用t来表示Q).(3)、当汽车行驶12小时,邮箱还剩多少升油?20. 如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.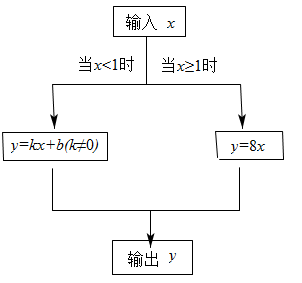
输人x
…
-6
-4
-2
0
2
…
输出y
…
-6
-2
2
6
16
…
根据以上信息,解答下列问题:
(1)、当输入的x值为1时,输出的y值为;(2)、求k,b的值;(3)、当输出的y值为0时,求输入的x值.21. 为合理安排进、离校时间,学校调查小组对某一天八年级学生上学、放学途中的用时情况进行了调查.本次调查在八年级随机抽取了名学生,建立以上学途中用时为横坐标、放学途中用时为纵坐标的平面直角坐标系,并根据调查结果画出相应的点,如图所示: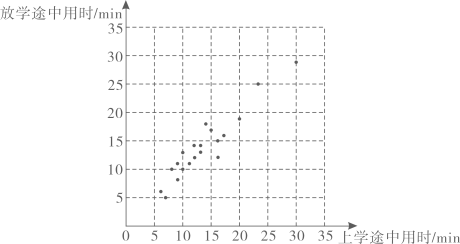 (1)、根据图中信息,下列说法中正确的是(写出所有正确说法的序号):
(1)、根据图中信息,下列说法中正确的是(写出所有正确说法的序号):①这名学生上学途中用时都没有超过;
②这名学生上学途中用时在以内的人数超过一半;
③这名学生放学途中用时最短为;
④这名学生放学途中用时的中位数为 .
(2)、已知该校八年级共有名学生,请估计八年级学生上学途中用时超过的人数(3)、调查小组发现,图中的点大致分布在一条直线附近.请直接写出这条直线对应的函数表达式并说明实际意义.22. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.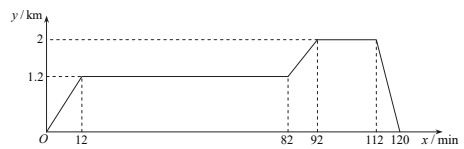
已知学生公寓、阅览室、超市依次在同一条直线上,阅览室离学生公寓 , 超市离学生公寓 , 小琪从学生公寓出发,匀速步行了到阅览室;在阅览室停留后,匀速步行了到超市;在超市停留后,匀速骑行了返回学生公寓.给出的图象反映了这个过程中小琪离学生公寓的距离与离开学生公寓的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开学生公寓的时间/
5
8
50
87
112
离学生公寓的距离/
0.5
1.6
(2)、填空:①阅览室到超市的距离为;
②小琪从超市返回学生公寓的速度为;
③当小琪离学生公寓的距离为时,他离开学生公寓的时间为 .
(3)、当时,请直接写出y关于x的函数解析式.23. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
 (1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?24. 图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示.
(1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?24. 图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示.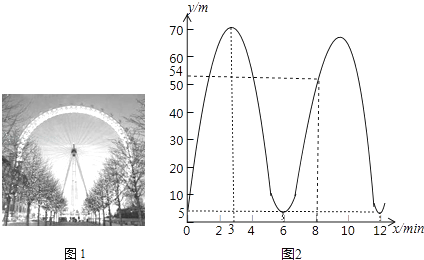 (1)、根据图2填表:
(1)、根据图2填表:x(min)
0
3
6
8
12
…
y(m)
…
(2)、变量y是x的函数吗?为什么?(3)、根据图中的信息,请写出摩天轮的直径.25. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:x(b)
……
11
12
13
14
15
16
17
18
……
y(cm)
……
189
137
103
80
101
133
202
260
……
(数据来自某海举研究所)
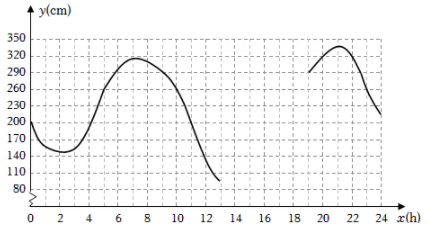 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?