备考2024年浙江中考数学一轮复习专题11.2一元二次方程 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
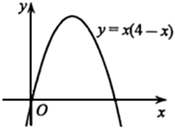
1. 某品牌新能源汽车2020年的销售量为20万辆,随着消费人群的不断增多,该品牌新能源汽车的销售量逐年递增,2022年的销售量比2020年增加了31.2万辆.如果设从2020年到2022年该品牌新能源汽车销售量的平均年增长率为x , 那么可列出方程是( )A、20(1+2x)=31.2 B、20(1+2x)-20=31.2 C、20(1+x)2=31.2 D、20(1+x)2-20=31.22. 若关于x的方程x2+6x+c=0有两个相等的实数根,则c的值是( )A、36 B、-36 C、9 D、-93. 若是方程的两个根,则( )A、 B、 C、 D、4. 已知x1 , x2是关于x的方程x2+bx﹣3=0的两根,且满足x1+x2﹣3x1x2=5,那么b的值为( )A、4 B、﹣4 C、3 D、﹣35. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、6. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个7. 若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.若关于的二次函数(为常数,)总有两个不同的倍值点,则的取值范围是( )A、 B、 C、 D、8. 如图,现要在抛物线 上找点 ,针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若 ,则点P的个数为0;
乙:若 ,则点P的个数为1;
丙:若 ,则点P的个数为1.
下列判断正确的是( )
 A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对9. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )
A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对9. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )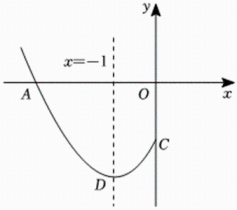 A、个 B、个 C、个 D、个10. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”,已知点 , 有下列结论:
A、个 B、个 C、个 D、个10. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”,已知点 , 有下列结论:①点 , 都是点的“倍增点”;
②若直线上的点A是点的“倍增点”,则点的坐标为;
③抛物线上存在两个点是点的“倍增点”;
④若点是点的“倍增点”,则的最小值是 .
其中,正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题(每题3分,共18分)
-
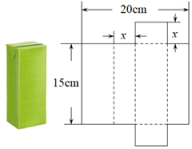
11. 为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为 , 根据题意,请列出方程 .12. 某网络学习平台2019年的新注册用户数为100万,2021年的新注册用户数为169万,设新注册用户数的年平均增长率为x(x>0),则x= (用百分数表示).13. 若关于的方程有两个不相等的实数根,则的取值范围是 .14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
 15. 若(为实数),则的最小值为.16. 如图是一块矩形菜地ABCD,AB=a(m),AD=b(m),面积为.现将边AB增加1m.
15. 若(为实数),则的最小值为.16. 如图是一块矩形菜地ABCD,AB=a(m),AD=b(m),面积为.现将边AB增加1m.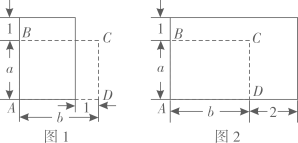 (1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.
(1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.三、解答题(共6题,共35分)
-
17. 解方程:18. 设一元二次方程 . 在下面的四组条件中选择其中一组的值,使这个方程有两个不相等的实数根,并解这个方程.
①;②;③;④ .
19. 已知关于x的一元二次方程 .(1)、求证:无论m取何值时,方程都有两个不相等的实数根;(2)、设该方程的两个实数根为a,b,若 , 求m的值.20. 先化简,再求值: , 其中a , b是方程的两个根.21. 若a为一元二次方程x2- x=-4的较大的个根,b为一元二次方程(y-4)2=18的较小的一个根,求a-b的值.22. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .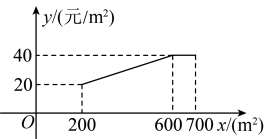 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?四、实践探究题(共4题,共37分)
-
23. 我们规定:对于任意实数a、b、c、d有 , 其中等式右边是通常的乘法和减法运算,如: .(1)、求的值;(2)、已知关于x的方程有两个实数根,求m的取值范围.24. 阅读材料:
材料1:关于x的一元二次方程的两个实数根和系数a,b,c有如下关系: , .
材料2:已知一元二次方程的两个实数根分别为m,n,求的值.
解:∵m,n是一元二次方程的两个实数根,
∴ .
则 .
根据上述材料,结合你所学的知识,完成下列问题:
(1)、应用:一元二次方程的两个实数根为 , 则 , ;(2)、类比:已知一元二次方程的两个实数根为m,n,求的值;(3)、提升:已知实数s,t满足且 , 求的值.25. 阅读材料,解答问题:材料1
为了解方程 , 如果我们把看作一个整体,然后设 , 则原方程可化为 , 经过运算,原方程的解为 , . 我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足 , , 且 , 显然m,n是方程的两个不相等的实数根,由书达定理可知 , .
根据上述材料,解决以下问题:
(1)、直接应用:方程的解为;
(2)、间接应用:已知实数a,b满足: , 且 , 求的值;
(3)、拓展应用:已知实数m,n满足: , 且 , 求的值.
26. 【观察思考】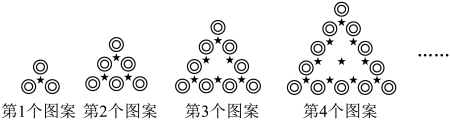
【规律发现】
请用含的式子填空:
(1)、第个图案中“ ”的个数为; (2)、第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , ……,第个图案中“★”的个数可表示为 .(3)、【规律应用】
”的个数为; (2)、第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , 第个图案中“★”的个数可表示为 , ……,第个图案中“★”的个数可表示为 .(3)、【规律应用】
结合图案中“★”的排列方式及上述规律,求正整数 , 使得连续的正整数之和等于第个图案中“ ”的个数的倍.
”的个数的倍.