备考2024年浙江中考数学一轮复习专题11.1一元二次方程基础夯实

试卷更新日期：2024-02-24 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列方程是一元二次方程的是（）

A、3x²+y＝2 B、x²﹣ $\frac{1}{x}$ +1＝0 C、x²﹣5x＝3 D、x﹣3y+1＝0

查看试题解析
2. 有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？设每轮传染中平均一个人传染了x个人，下列所列方程正确的是（）

A、 ${(1 + x)}^{2} = 121$ B、 $1 + x + x^{2} = 121$ C、 $1 + x + {(x + 1)}^{2} = 121$ D、 $1 + x + 2 (x + 1) = 121$

查看试题解析
3. 根据下列表格对应值：

x

2.1

2.2

2.3

2.4

2.5

ax²+bx+c

﹣0.12

﹣0.03

﹣0.01

0.06

0.18

判断关于x的方程ax²+bx+c＝0（a≠0）的一个解x的范围是（）

A、2.1＜x＜2.2 B、2.2＜x＜2.3 C、2.3＜x＜2.4 D、2.4＜x＜2.5

查看试题解析
4. 用配方法解一元二次方程x²+4x﹣5=0，此方程可变形为（　　）

A、（x+2）²=9 B、（x﹣2）²=9 C、（x+2）²=1 D、（x﹣2）²=1

查看试题解析
5. 用因式分解法解下列方程，变形正确的是（）

A、(3x-3)(3x-4)=0，于是3x-3=0或3x-4=0 B、(x+3)(x-1)=1，于是x+3=1或x-1=1 C、(x-2)(x-3)=6，于是x-2=2或x-3=3 D、x(x+2)=0，于是x+2=0

查看试题解析
6. 关于x的一元二次方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤﹣ $\frac{9}{4}$ B、k≤﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k≥﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
7. $x = \frac{- 5 \pm \sqrt{5^{2} + 4 \times 3 \times 1}}{2 \times 3}$ 是下列哪个一元二次方程的根（）

A、 $3 x^{2} + 5 x + 1 = 0$ B、 $3 x^{2} - 5 x - 1 = 0$ C、 $3 x^{2} + 5 x - 1 = 0$ D、 $3 x^{2} - 5 x + 1 = 0$

查看试题解析
8. 关于 $x$ 的一元二次方程 $x^{2} + 2 x - 2 t + 3 = 0$ 的两个实数根分别是 $m ， n$ ，则 $(m - t) (n^{2} + 3)$ 的最大值是（）

A、 $- 10$ B、 $- 8$ C、 $- 6$ D、 $- 2$

查看试题解析
9. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
10. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = (2 a x_{0} + b)^{2}$ ；⑤存在实数 $m ， n (m \neq n)$ ，使得 $a m^{2} + b m + c = a n^{2} + b n + c$ ．
其中正确的（）

A、只有①②④ B、只有①②④⑤ C、①②③④⑤ D、只有①②③

查看试题解析

二、填空题（每题3分，共18分）

11. 若方程 $(m - 1) x^{2} - 4 x + 3 = 0$ 是一元二次方程，当m满足条件．

查看试题解析
12. 构造一个一元二次方程，要求：①常数项不为0；②有一个根为-1.这个一元二次方程可以是(写出一个即可).

查看试题解析
13. 已知关于x的一元二次方程x²+mx-2=0的一个根为-1，则m的值为，另一个根为.

查看试题解析
14. 若M＝2x²-12x+15，N＝x²-8x+11，则M与N的大小关系为．

查看试题解析
15. 若一元二次方程x²﹣3x﹣1=0的两根分别为x₁、x₂ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ = ．

查看试题解析
16. 已知关于x的方程kx²+（1-k）x-1=0，有下列说法：①当k=0时，方程无解；②当k=1时，方程有一个实数解；③当k=-1时，方程有两个相等的实数解；④此方程总有实数解．其中正确的是．

查看试题解析

三、计算题（共2题，共15分）

17. 用适当的方法解下列方程：

(1)、 ${(x + 2)}^{2} - 25 = 0 ，$

(2)、x²+4x-5=0.

(3)、2x²+1=3x.

(4)、 $3 (x - 2) + x^{2} - 2 x = 0 .$

查看试题解析
18. 解方程： $x^{2} - 2 x - \frac{6}{x^{2} - 2 x} = 1$ ．

查看试题解析

四、解答题（共5题，共28分）

19. 若关于x的一元二次方程 $x^{2} - 6 x$ -k-1=0与 $x^{2} - k x - 7 = 0$ 仅有一个公共的实数根，求k的值和公共的实数根。

查看试题解析
20. 已知a，b是整数，关于x的方程x²-ax+3-6=0有两个不相等的实数根，x²+(6-a)x+7-b=0有两个相等的实数根，x²+(4-a)x+5-b=0没有实数根，求a，b的值．

查看试题解析
21. 已知关于x的方程 $x^{2} + (3 k - 2) x - 6 k = 0$ ．

(1)、求证：无论 $k$ 取何实数值，方程总有实数根．

(2)、若等腰三角形 $A B C$ 的一边长 $a = 6$ ，另两边长 $b ， c$ 恰好是这个方程的两个根，求 $△ A B C$ 的周长．

查看试题解析
22. 如图，用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈，每个矩形都有一个1米的门，墙的最大可用长度为30米．

(1)、如果羊圈的总面积为300平方米，求边 $A B$ 的长；

(2)、羊圈的总面积能为500平方米吗？若能，请求出边 $A B$ 的长；若不能，说明理由．

查看试题解析
23. $2022$ 年卡塔尔世界杯足球赛开战，很多商家都紧紧把握这一商机，赛场内外随处可见“中国制造”的身影，某商家销售一批“中国制造”的吉祥物“拉伊卜”毛绒玩具，已知每个毛绒玩具“拉伊卜”的成本为 $40$ 元，销售单价不低于成本价，且不高于成本价的 $1.8$ 倍，在销售过程中发现，毛绒玩具“拉伊卜”每天的销售量 $y ($ 个 $)$ 与销售单价 $x ($ 元 $)$ 满足如图所示的一次函数关系．

(1)、求 $y$ 与 $x$ 的函数关系式，并直接写出自变量 $x$ 的取值范围；

(2)、每个毛绒玩具“拉伊卜”的售价为多少元时，该商家每天的销售利润为 $2400$ 元？

(3)、当毛绒玩具“拉伊卜”的销售单价为多少元时，该商家每天获得的利润最大？最大利润是多少元？

查看试题解析

五、实践探究题（共3题，共29分）

24. 如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知 $A E = \sqrt{2}$ ，这时我们把关于x的形如 $a x^{2} + \sqrt{2} c x + b = 0$ 的一元二次方程称为“勾系一元二次方程”．
请解决下列问题：

(1)、写出一个“勾系一元二次方程”；

(2)、求证：关于x的“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 必有实数根；

(3)、若x＝﹣1是“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 的一个根，且四边形ACDE的周长是6 $\sqrt{2}$ ，求△ABC面积．

查看试题解析
25. 阅读下列材料：
配方法是初中数学中经常用到的一个重要方法，学好配方法对我们学习数学有很大的帮助 $.$ 所谓配方，就是将某一个多项式变形为一个完全平方式，但变形一定要保证恒等，即配方前后式子的值不变．
例如：
解方程 $x^{2} - 2 x - 3 = 0$ ，则有 $x^{2} - 2 x + 1 - 1 - 3 = 0$ ， $∴ (x - 1)^{2} = 4$ ，解得 $x_{1} = 3$ ， $x_{2} = - 1$ ．
已知 $x^{2} - 2 x + y^{2} + 4 y + 5 = 0$ ，求 $x$ ， $y$ 的值，则有 $(x^{2} - 2 x + 1) + (y^{2} + 4 y + 4) = 0$ ， $∴ (x - 1)^{2} + (y + 2)^{2} = 0$ ，解得 $x = 1$ ， $y = - 2$ ，
根据以上材料解答下列各题：

(1)、若 $x^{2} - 4 x + y^{2} + 6 y + 13 = 0$ ，求 $(x + y)^{- 2011}$ 的值；

(2)、无论 $a$ 取何值，关于 $x$ 的一元二次方程 $x^{2} - (a - 3) x - a = 0$ 总有两个不相等的实数根；

(3)、解方程： $x^{2} - 360 x + 32000 = 0$ ；

(4)、若 $a$ ， $b$ ， $c$ 表示 $△ A B C$ 的三边长，且 $a^{2} + b^{2} + c^{2} - a c - a b - b c = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析

26.

如何利用闲置纸板箱制作储物盒
素材 1	如图1是小琴家需要设置储物盒的区域，该区域可以近似看成一个长方体，底面尺寸如图2所示.
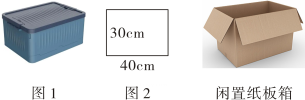
素材 2	如图3、图4是利用闲置纸板箱拆解出的①，②两种一边均为a(cm)(a<50)的矩形纸板.
	纸板①(单位：cm)			纸板②(单位：cm)

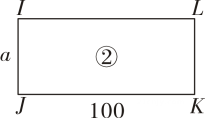
	小琴分别将纸板①和②以不同的方式制作储物盒.
	纸板①的制作方式			纸板②的制作方式
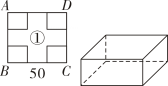
	裁去角上4个相同的小正方形，折成一个无盖长方体储物盒.			将纸片四个角裁去4个相同的小矩形，折成一个有盖的长方体储物盒。
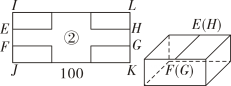
目标 1	熟悉材料			⑴若按照纸板①的制作方式制成的储物盒恰好完全放入储物区域，则长方形纸板的宽a= cm.
目标 2		利用目标1计算所得的数据a，进行进一步探究.
		初步应用	⑵按照纸板①的制作方式，为了更方便地放入或取出储物盒，盒子四周需要留出一定的空间，当储物盒的底面积是936cm²时，求储物盒的容积.
		储物收纳	⑶按照纸板②的制作方式制作储物盒，EF和HG两边恰好重合且无重叠部分，盒子的底面积为702cm².家里一个玩具机械狗的尺寸如图所示，请通过计算判断该机械狗能否完全放入储物盒.

查看试题解析

x	2.1	2.2	2.3	2.4	2.5
ax²+bx+c	﹣0.12	﹣0.03	﹣0.01	0.06	0.18

备考2024年浙江中考数学一轮复习专题11.1一元二次方程 基础夯实

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、计算题（共2题，共15分）

四、解答题（共5题，共28分）

五、实践探究题（共3题，共29分）

备考2024年浙江中考数学一轮复习专题11.1一元二次方程基础夯实