备考2024年浙江中考数学一轮复习专题10.2不等式与不等式组 真题集训
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 小霞原有存款52元,小明原有存款70元从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为( )A、52+15n>70+12n B、52+15n<70+12n C、52+12n>70+15n D、52+12n<70+15n2. 已知四个实数 , , , ,若 , ,则( )A、 B、 C、 D、3. 不等式组的解在数轴上表示正确的是( )A、
 B、
B、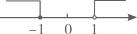 C、
C、 D、
D、 4. 不等式组 , 的解集是( )A、 B、无解 C、 D、5. 解不等式组时,不等式①②的解集在同一条数轴上表示正确是( )A、
4. 不等式组 , 的解集是( )A、 B、无解 C、 D、5. 解不等式组时,不等式①②的解集在同一条数轴上表示正确是( )A、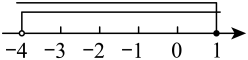 B、
B、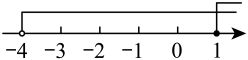 C、
C、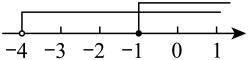 D、
D、 6. 已知不等式组的解集是 , 则=( )A、0 B、-1 C、1 D、20237. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且8. 已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )A、R至少2000Ω B、R至多2000Ω C、R至少24.2Ω D、R至多24.2Ω9. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
6. 已知不等式组的解集是 , 则=( )A、0 B、-1 C、1 D、20237. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且8. 已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )A、R至少2000Ω B、R至多2000Ω C、R至少24.2Ω D、R至多24.2Ω9. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )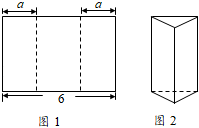 A、1 B、2 C、3 D、410. 如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )
A、1 B、2 C、3 D、410. 如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )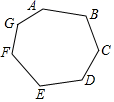 A、C、E B、E、F C、G、C、E D、E、C、F
A、C、E B、E、F C、G、C、E D、E、C、F二、填空题(每题4分, 共24分)
-
11. 不等式组 的解为.12. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.13. 若关于x的一元一次不等式组 , 至少有2个整数解,且关于y的分式方程有非负整数解,则所有满足条件的整数a的值之和是 .14. 已知非负实数 , , 满足 ,设 的最大值为 ,最小值为 ,则 的值为 .15. 如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程是关于x的不等式组的关联方程,则n的取值范围是 .16. 规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是 . (写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
三、计算题(共8分)
-
17.(1)、解方程组(2)、解不等式组
四、解答题(共7题,共58分)
-
18. 在下面给出的三个不等式中,请你任选两个组成一个不等式组,解这个不等式组,并把解集表示在数轴上.
①2x﹣1<7;②5x﹣2>3(x+1);③x+3≥1﹣x.
 19. 解不等式组并将其解集在数轴上表示出来.
19. 解不等式组并将其解集在数轴上表示出来. 20. 为丰富学生课余生活,提高学生运算能力,数学小组设计了如下的解题接力游戏:(1)、解不等式组:;(2)、当m取(1)的一个整数解时,解方程.21. 某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆120米.
20. 为丰富学生课余生活,提高学生运算能力,数学小组设计了如下的解题接力游戏:(1)、解不等式组:;(2)、当m取(1)的一个整数解时,解方程.21. 某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆120米.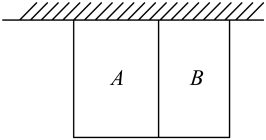 (1)、设计一个使花园面积最大的方案,并求出其最大面积;(2)、在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?22. 如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车.第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)、设计一个使花园面积最大的方案,并求出其最大面积;(2)、在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?22. 如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车.第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时. (1)、问第一班上行车到 站、第一班下行车到 站分别用时多少?(2)、若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式.(3)、一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米/小时,求 满足的条件.23. “人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.(1)、求两种型号玩具的单价各是多少元?
(1)、问第一班上行车到 站、第一班下行车到 站分别用时多少?(2)、若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式.(3)、一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米/小时,求 满足的条件.23. “人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.(1)、求两种型号玩具的单价各是多少元?根据题意,甲、乙两名同学分别列出如下方程:
甲: , 解得 , 经检验是原方程的解.
乙: , 解得 , 经检验是原方程的解.
则甲所列方程中的表示 , 乙所列方程中的表示;
(2)、该经营者准备用1350元以原单价再次购进这两种型号的玩具共200个,则最多可购进型玩具多少个?24. 2022年8月27日至29日,以“新能源、新智造、新时代”为主题的世界清洁能源装备大会在德阳举行.大会聚焦清洁能源装备产业发展热点和前瞻性问题,着力实现会展聚集带动产业聚集.其中德阳清洁能源装备特色小镇位于德阳经济技术开发区,规划面积平方公里,计划2025年基本建成.若甲、乙两个工程队计划参与修建“特色小镇”中的某项工程,已知由甲单独施工需要18个月完成任务,若由乙先单独施工2个月,再由甲、乙合作施工10个月恰好完成任务.承建公司每个月需要向甲工程队支付施工费用8万元,向乙工程队支付施工费用5万元.(1)、乙队单独完工需要几个月才能完成任务?(2)、为保证该工程在两年内完工,且尽可能的减少成本,承建公司决定让甲、乙两个工程队同时施工,并将该工程分成两部分,甲队完成其中一部分工程用了a个月,乙队完成另一部分工程用了b个月,已知甲队施工时间不超过6个月,乙队施工时间不超过24个月,且a,b为正整数,则甲乙两队实际施工的时间安排有几种方式?哪种安排方式所支付费用最低?
-