备考2024年浙江中考数学一轮复习专题10.1不等式与不等式组 基础夯实
试卷更新日期:2024-02-24 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 现有下列各式:①-3<0;②x+3y≥0;③x=3;④x2+xy+y2 . 其中不等式有( )A、1个 B、2个 C、3个 D、4个2. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、3. 若 , 则下列不等式成立的是( )A、 B、 C、 D、4. 如果不等式的解集为 , 则必须满足的条件是 ( )A、 B、 C、 D、5. 下列数轴上,正确表示不等式的解集的是( )A、
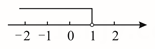 B、
B、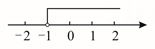 C、
C、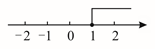 D、
D、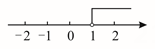 6. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、
6. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、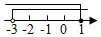 B、
B、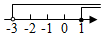 C、
C、 D、
D、 7. 2023年9月23日,第19届亚运会将在我国杭州市举办.为此,某校举行了关于杭州亚运会的知识竞赛.现共有30道选择题,答对一题得10分,若答错或不答一道题,则扣3分.要使总得分不少于70分则应该至少答对几道题?若设答对x题,则根据题意可列不等式为( )A、 B、 C、 D、8. 把一些书分给几名同学,若每人分9本,则书本有剩余,条件*.若根据题意,设有名同学,可得到符合题意的不等式 , 则“条件*”可以是( )A、每人分5本,则剩余3本 B、每人分5本,则剩余的书可多分给3个人 C、每人分5本,则还差3本 D、其中一个人分5本,则其他同学每人可分3本9. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了两次才停止,那么的取值范围是( )
7. 2023年9月23日,第19届亚运会将在我国杭州市举办.为此,某校举行了关于杭州亚运会的知识竞赛.现共有30道选择题,答对一题得10分,若答错或不答一道题,则扣3分.要使总得分不少于70分则应该至少答对几道题?若设答对x题,则根据题意可列不等式为( )A、 B、 C、 D、8. 把一些书分给几名同学,若每人分9本,则书本有剩余,条件*.若根据题意,设有名同学,可得到符合题意的不等式 , 则“条件*”可以是( )A、每人分5本,则剩余3本 B、每人分5本,则剩余的书可多分给3个人 C、每人分5本,则还差3本 D、其中一个人分5本,则其他同学每人可分3本9. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了两次才停止,那么的取值范围是( ) A、 B、 C、 D、10. 规定:对于任意实数x,通常用[x]表示不超过x的最大整数,如:[π]=3,[2]=2,[-2.1]=-3给出下列结论:①[-x]=-x;②若[x]=n,则x的取值范围是n≤x<n+1;③当-1<x<1时,[1+x]+[1-x]的值为1或2;④x=-2.75是方程4x-2[x]+5=0的唯一解.其中正确结论的序号是( )A、①② B、②③ C、①③ D、③④
A、 B、 C、 D、10. 规定:对于任意实数x,通常用[x]表示不超过x的最大整数,如:[π]=3,[2]=2,[-2.1]=-3给出下列结论:①[-x]=-x;②若[x]=n,则x的取值范围是n≤x<n+1;③当-1<x<1时,[1+x]+[1-x]的值为1或2;④x=-2.75是方程4x-2[x]+5=0的唯一解.其中正确结论的序号是( )A、①② B、②③ C、①③ D、③④二、填空题(每题3分,共18分)
-
11. 若 是关于 的一元一次不等式,则 的值为。12. 若不等式组无解,则a的取值范围是 .13. 若关于x的不等式组的解为x<-2,且关于y的分式方程的解为正数,则所有满足条件的整数a的值之和为.14. 对非负实数x“四舍五入”到个位的值记为(x),即当n为自然数时,若n-0.5≤x<n+0.5,则(x)=n,如(1.34)=1,(4.86)=5.若(0.5x-1)=6,则实数x的取值范围是.15. 已知 的两条边长分别为3和5,且第三边的长c为整数,则c的取值可以为.16. 如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由8个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数a的值为 .
a
a2﹣1
﹣a
﹣a2
2﹣a
1﹣a2
a﹣2
a2
三、计算题(共9分)
-
17. 解下列不等式(组):(1)、(2)、(3)、
四、解答题(共7题,共51分)
-
18. 解不等式组 , 可按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
 (4)、原不等式组的解集为:.19. 已知不等式的最小正整数解是方程的解,求的值.20. 定义新运算:对于任意实数a , b都有 , 如: , 请求出不等式的正整数解.21. 为培养大家的阅读能力,我校初一年级购进《朝花夕拾》和《西游记》两种书籍,花费分别是14000元和7000元,已知《朝花夕拾》的订购单价是《西游记》的订购单价的1.4倍,并且订购的《朝花夕拾》的数量比《西游记》的数量多300本.(1)、求我校初一年级订购的两种书籍的单价分别是多少元;(2)、我校初一年级某班计划再订购这两种书籍共10本来备用,其中《朝花夕拾》订购数量不低于3本,且两种书总费用不超过124元,求这个班订购这两种书籍有多少种方案?按照这些方案订购最低总费用为多少元?22. 为推进美丽乡村建设,改善人居环境,创建美丽家园.我市甲、乙两工厂积极生产了某种建设物资共800吨,甲工厂的生产量是乙工厂的2倍少100吨,这批建设物资将运往A地420吨,B地380吨,运费如下:(单位:吨)
(4)、原不等式组的解集为:.19. 已知不等式的最小正整数解是方程的解,求的值.20. 定义新运算:对于任意实数a , b都有 , 如: , 请求出不等式的正整数解.21. 为培养大家的阅读能力,我校初一年级购进《朝花夕拾》和《西游记》两种书籍,花费分别是14000元和7000元,已知《朝花夕拾》的订购单价是《西游记》的订购单价的1.4倍,并且订购的《朝花夕拾》的数量比《西游记》的数量多300本.(1)、求我校初一年级订购的两种书籍的单价分别是多少元;(2)、我校初一年级某班计划再订购这两种书籍共10本来备用,其中《朝花夕拾》订购数量不低于3本,且两种书总费用不超过124元,求这个班订购这两种书籍有多少种方案?按照这些方案订购最低总费用为多少元?22. 为推进美丽乡村建设,改善人居环境,创建美丽家园.我市甲、乙两工厂积极生产了某种建设物资共800吨,甲工厂的生产量是乙工厂的2倍少100吨,这批建设物资将运往A地420吨,B地380吨,运费如下:(单位:吨)生产厂
A
B
甲
25
20
乙
15
24
(1)、求甲、乙两厂各生产了这批建设物资多少吨?(2)、设这批物资从甲工厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,写出x的取值范围并设计使总运费最少的调运方案;(3)、由于甲工厂到A地的路况得到了改善,缩短了运输距离和运输时间,运费每吨降低m元(0<m≤15),其余路线运费不变.若到A,B两市的总运费的最小值不小于14020元,求m的取值范围.23. 定义:规定 , 例如: , .(1)、 ;(2)、解不等式组:;(3)、若关于的不等式组恰好有三个整数解,则的取值范围为 .24. 我们定义,关于同一个未知数的不等式A和B,两个不等式的解集相同,则称A与B为同解不等式.(1)、若关于x的不等式A: , 不等式B:是同解不等式,求a的值;(2)、若关于x的不等式C: , 不等式D:是同解不等式,其中m,n是正整数,求m,n的值;(3)、若关于x的不等式P: , 不等式Q:是同解不等式,试求关于x的不等式的解集.五、实践探究题(共12分)
-
25. 新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程x-1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x-1=3是不等式组的“关联方程”.(1)、在方程①2(x+1)-x=-3;②-1=x;③2x-7=0中,不等式组的“关联方程”是(填序号)(2)、关于x的方程2x-k=6是不等式组的“关联方程”,求k的取值范围;(3)、若关于x的方程-3m=0是关于x的不等式组的“关联方程”,且此时不等式组有3个整数解,试求m的取值范围.
-