备考2024年浙江中考数学一轮复习专题8.2一元一次方程真题集训

试卷更新日期：2024-02-24 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列说法中，正确的是（）

A、若 $a c = b c$ ，则 $a = b$ B、若 $a^{2} = b^{2}$ ，则 $a = b$ C、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ D、若 $- \frac{1}{3} x = 6$ ，则 $x = 2$

查看试题解析
2. 若代数式 $x + 2$ 的值为7，则x等于（）

A、9 B、 $- 9$ C、5 D、 $- 5$

查看试题解析
3. 关于 $x$ 的一元一次方程 $2 x^{a - 2} + m = 4$ 的解为 $x = 1$ ，则 $a + m$ 的值为（）

A、9 B、8 C、5 D、4

查看试题解析
4. 关于x的一元一次方程 $2 x + m = 5$ 的解为 $x = 1$ ，则m的值为（）

A、3 B、 $- 3$ C、7 D、 $- 7$

查看试题解析
5. 解方程 $- 2 (2 x + 1) = x$ ，以下去括号正确的是（）

A、 $- 4 x + 1 = - x$ B、 $- 4 x + 2 = - x$ C、 $- 4 x - 1 = x$ D、 $- 4 x - 2 = x$

查看试题解析
6. 甲、乙两运动员在长为 $100 m$ 的直道 $A B$ （ $A$ ， $B$ 为直道两端点）上进行匀速往返跑训练，两人同时从 $A$ 点起跑，到达 $B$ 点后，立即转身跑向 $A$ 点，到达 $A$ 点后，又立即转身跑向 $B$ 点……若甲跑步的速度为 $5 m / s$ ，乙跑步的速度为 $4 m / s$ ，则起跑后 $100 s$ 内，两人相遇的次数为（）

A、5 B、4 C、3 D、2

查看试题解析
7. 已知某商店有两件进价不同的运动衫都卖了160元，其中一件盈利60%，另一件亏损20%，在这次买卖中这家商店（）

A、不盈不亏 B、盈利20元 C、盈利10元 D、亏损20元

查看试题解析
8. 我国古代数学著作《孙子算经》中有这样一道题，原文如下：今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽，问：城中家几何？大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完，问：城中有多少户人家？在这个问题中，城中人家的户数为（）

A、25 B、75 C、81 D、90

查看试题解析
9. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一，书中记载一道问题：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天可以追上慢马？若设快马x天可以追上慢马，则下列方程正确的是（）

A、 $240 x + 150 x = 150 \times 12$ B、 $240 x - 150 x = 240 \times 12$ C、 $240 x + 150 x = 240 \times 12$ D、 $240 x - 150 x = 150 \times 12$

查看试题解析
10. 《孙子算经》记载：“今有木，不知长短．引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”（尺、寸是长度单位，1尺＝10寸）．意思是，现有一根长木，不知道其长短．用一根绳子去度量长木，绳子还剩余4.5尺；将绳子对折再度量长木，长木还剩余1尺．问长木长多少？设长木长为x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x - 4.5) = x + 1$ D、 $\frac{1}{2} (x - 4.5) = x - 1$

查看试题解析

二、填空题

11. 点Q的横坐标为一元一次方程 $3 x + 7 = 32 - 2 x$ 的解，纵坐标为 $a + b$ 的值，其中a，b满足二元一次方程组 ${\begin{array}{l} 2 a - b = 4 \\ - a + 2 b = - 8 \end{array}$ ，则点Q关于y轴对称点 $Q^{'}$ 的坐标为．

查看试题解析
12. 已知a，b，c为 $△ A B C$ 的三边长.b，c满足 ${(b - 2)}^{2} + | c - 3 | = 0$ ，且a为方程 $| x - 4 | = 2$ 的解，则 $△ A B C$ 的形状为三角形.

查看试题解析
13. 某酒店客房都有三人间普通客房，双人间普通客房，收费标准为：三人间150元/间，双人间140元/间．为吸引游客，酒店实行团体入住五折优惠措施，一个46人的旅游团，优惠期间到该酒店入住，住了一些三人间普通客房和双人间普通客房，若每间客房正好住满，且一天共花去住宿费1310元，则该旅游团住了三人间普通客房和双人间普通客房共间；

查看试题解析
14. 某企业有 $A ， B$ 两条加工相同原材料的生产线．在一天内， $A$ 生产线共加工 $a$ 吨原材料，加工时间为 $(4 a + 1)$ 小时；在一天内， $B$ 生产线共加工 $b$ 吨原材料，加工时间为 $(2 b + 3)$ 小时．第一天，该企业将5吨原材料分配到 $A ， B$ 两条生产线，两条生产线都在一天内完成了加工，且加工时间相同，则分配到 $A$ 生产线的吨数与分配到 $B$ 生产线的吨数的比为．第二天开工前，该企业按第一天的分配结果分配了5吨原材料后，又给 $A$ 生产线分配了 $m$ 吨原材料，给 $B$ 生产线分配了 $n$ 吨原材料．若两条生产线都能在一天内加工完各自分配到的所有原材料，且加工时间相同，则 $\frac{m}{n}$ 的值为．

查看试题解析
15. 古代中国的数学专著《九章算术》中有一题：“今有生丝三十斤，千之，耗三斤十二两．今有干丝一十二斤，问生丝几何？“意思是：“今有生丝30斤，干燥后耗损3斤12两(古代中国1斤等于16两)．今有干丝12斤，问原有生丝多少？”则原有生丝为斤．

查看试题解析
16. 小伟用撬棍撬动一块大石头，已知阻力和阻力臂分别为1000N和0.6m，当动力臂由1.5m增加到2m时，撬动这块石头可以节省N的力．（杜杆原理：阻力 $\times$ 阻力臂 $＝$ 动力 $\times$ 动力臂）

查看试题解析

三、综合题

17. 计算：(-6) ×( $\frac{2}{3}$ -■)-2³ ．
圆圆在做作业时，发现题中有一个数字被墨水污染了。

(1)、如果被污染的数字是 $\frac{1}{2}$ ．请计算(-6)×( $\frac{2}{3}$ - $\frac{1}{2}$ )-2³ ．

(2)、如果计算结果等于6，求被污染的数字．

查看试题解析
18. 对于任意实数a，b，定义一种新运算： $a ※ b = {\begin{array}{l} a - b & (a \geq 2 b) \\ a + b - 6 & (a < 2 b) \end{array}$ ，例如： $3 ※ 1 = 3 - 1 = 2$ ， $5 ※ 4 = 5 + 4 - 6 = 3$ ．根据上面的材料，请完成下列问题：

(1)、 $4 ※ 3 =$ ， $(- 1) ※ (- 3) =$ ；

(2)、若 $(3 x + 2) ※ (x - 1) = 5$ ，求x的值．

查看试题解析
19. 某磁性飞镖游戏的靶盘如图．珍珍玩了两局，每局投10次飞镖，若投到边界则不计入次数，需重新投，计分规则如下：
投中位置
A区
B区
脱靶
一次计分（分）
3
1
$- 2$
在第一局中，珍珍投中A区4次，B区2次，脱靶4次．

(1)、求珍珍第一局的得分；

(2)、第二局，珍珍投中A区k次，B区3次，其余全部脱靶．若本局得分比第一局提高了13分，求k的值．

查看试题解析

四、解答题

20. 小红在解方程 $\frac{7 x}{3} = \frac{4 x - 1}{6} + 1$ 时，第一步出现了错误：

(1)、请在相应的方框内用横线划出小红的错误处.

(2)、写出你的解答过程.

查看试题解析
21. 某古镇为发展旅游产业，吸引更多的游客前往游览，助力乡村振兴，决定在“五一”期间对团队*旅游实行门票特价优惠活动，价格如下表：
购票人数 $m$ （人）
          $10 \leq m \leq 50$
          $51 \leq m \leq 100$
          $m > 100$
每人门票价（元）
60
50
40
*题中的团队人数均不少于10人
现有甲、乙两个团队共102人，计划利用“五一”假期到该古镇旅游，其中甲团队不足50人，乙团队多于50人．

(1)、如果两个团队分别购票，一共应付5580元，问甲、乙团队各有多少人？

(2)、如果两个团队联合起来作为一个“大团队”购票，比两个团队各自购票节省的费用不少于1200元，问甲团队最少多少人？

查看试题解析
22. 对联是中华传统文化的瑰宝，对联装裱后，如图所示，上、下空白处分别称为天头和地头，左、右空白处统称为边．一般情况下，天头长与地头长的比是 $6 ： 4$ ，左、右边的宽相等，均为天头长与地头长的和的 $\frac{1}{10}$ ．某人要装裱一副对联，对联的长为 $100 c m$ ，宽为 $27 c m$ ．若要求装裱后的长是装裱后的宽的4倍，求边的宽和天头长．（书法作品选自《启功法书》）

查看试题解析

23. 某公司专业生产某种产品，6月初（当月月历如图）接到一份求购5000件该产品的订单，要求本月底完成，7月1日按期交货．

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

经盘点目前公司已有该产品库存2855件，补充原材料后，从本月7日开始生产剩余数量的该产品，已知该公司除周六、周日正常休息外，每天的生产量相同．但因受高温天气影响，从本月10日开始，每天的生产量比原来减少了25件，截止到17日生产结束，库存总量达3830件．如果按照10日开始的生产速度继续生产该产品，能否按期完成订单？请说明理由．如果不能，请你给该公司生产部门提出一个合理的建议，以确保能按期交货．

查看试题解析

五、实践探究题

24. 学校数学兴趣小组利用机器人开展数学活动.在相距 $150$ 个单位长度的直线跑道 $A B$ 上，机器人甲从端点 $A$ 出发，匀速往返于端点 $A$ 、 $B$ 之间，机器人乙同时从端点 $B$ 出发，以大于甲的速度匀速往返于端点 $B$ 、 $A$ 之间.他们到达端点后立即转身折返，用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况，这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.

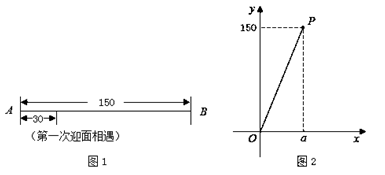(1)、【观察】
①观察图 $1$ ，若这两个机器人第一次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $30$ 个单位长度，则他们第二次迎面相遇时，相遇地点与点 $A$ 之间的距离为个单位长度；

②若这两个机器人第一次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $40$ 个单位长度，则他们第二次迎面相遇时，相遇地点与点 $A$ 之间的距离为个单位长度；

(2)、【发现】
设这两个机器人第一次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $x$ 个单位长度，他们第二次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $y$ 个单位长度.兴趣小组成员发现了 $y$ 与 $x$ 的函数关系，并画出了部分函数图象（线段 $O P$ ，不包括点 $O$ ，如图 $2$ 所示）.

① $a$ ＝；

②分别求出各部分图象对应的函数表达式，并在图 $2$ 中补全函数图象；

(3)、【拓展】
设这两个机器人第一次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $x$ 个单位长度，他们第三次迎面相遇时，相遇地点与点 $A$ 之间的距离为 $y$ 个单位长度.若这两个机器人第三次迎面相遇时，相遇地点与点 $A$ 之间的距离 $y$ 不超过 $60$ 个单位长度，则他们第一次迎面相遇时，相遇地点与点 $A$ 之间的距离 $x$ 的取值范围是.（直接写出结果）

查看试题解析

购票人数 $m$ （人）	$10 \leq m \leq 50$	$51 \leq m \leq 100$	$m > 100$
每人门票价（元）	60	50	40

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

投中位置	A区	B区	脱靶
一次计分（分）	3	1	$- 2$

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30