（华师大版）2023-2024学年度第二学期八年级数学第二十章 数据的整理与初步处理 单元测试
试卷更新日期：2024-02-23 类型：单元试卷
一、选择题（每题4分，共48分）
-
1. 数据-1，0，3，4，4的平均数是（ ）A、4 B、3 C、2.5 D、22. 5名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（ ）A、40% B、56% C、60% D、62%3. 有一组数据：2，2，4，5，7，这组数据的众数是（ ）A、2 B、4 C、5 D、74. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5 分)，则所打分数的众数为（ ）
课后延时服务的打分情况扇形统计图
A、5分 B、4分 C、3分 D、45%5. 在射击训练中，某队员的10次射击成绩如图，则这10次射击成绩的中位数(单位：环)和众数(单位：环)分别是（ ）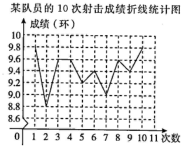
A、9.6，9.6 B、9.5，9.4 C、9.5，9.6 D、9.6，9.86. 期中考试后，班里有两位同学议论他们小组的数学成绩，小晖说：“我们组考分是 82 分的人最多”，小聪说：“我们组的7 位同学成绩排在最中间的恰好也是 82分”.上面两位同学的话中能反映出的统计量分别是（ ）A、众数和平均数 B、平均数和中位数 C、平均数和众数 D、众数和中位数7. 《义务教育课程标准(2022 年版)》首次把学生学会炒菜纳入劳动教育课程.某班有7 名学生已经学会炒的菜品的种数依次为 3，5，4，6，3，3，4，则这组数据的众数是（ ）A、3 B、4 C、5 D、68. 作为北京 2022 年冬季奥运会的吉祥物，冰墩墩很受欢迎.某玩具店一个星期销售冰墩墩玩具的数量如下：星期 一 二 三 四 五 六 日 玩具数量(件) 35 47 50 48 42 60 68 则这个星期该玩具店销售冰墩墩玩具的平均数(单位：件)和中位数(单位：件)分别是（ ）
A、48，47 B、50，47 C、50，48 D、48，509. 抽查某班10名同学的中考体育测试成绩如下表所示：成绩(分)
30
25
20
15
人数
2
x
y
1
若成绩的平均数是 23，中位数是 a，众数是b，则a -b的值为 （ ）
A、-5 B、-2.5 C、2.5 D、510. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数(单位： 环)．及方差s2(单位：环2)如下表所示，根据表中数据，要从中选择一 名成绩好且发挥稳定的运动员参加比赛，应选择（ ）甲
乙
丙
丁
9
8
9
9
S2
1.2
0.4
1.8
0.4
A、甲 B、乙 C、丙 D、丁11. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋设货架上原有鸡蛋质量(单位：g)的平均数和方差分别为 ， S2 ，该顾客选购的鸡蛋质量的平均数和方差分别为 ， ，则下列结论一定成立的是（ ）A、< B、 > C、S2> D、S2<12. 4月23日是世界读书日，学校举行“快乐阅读，健康成长”读书活动．小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量，数据如下表所示，则阅读课外书数量的中位数和众数分别是（ ）人数
6
7
10
7
课外书数量(本)
6
7
9
12
A、8本，9本 B、10本，9本 C、7本，12本 D、9本，9本二、填空题（每题4分，共24分）
-
13. 有5个不同的整数1，3，5，12，a，其中a是这组数据的中位数，则该组数据的平均数是.14. 已知一组数据如下表所示：
数据 37 38 39 40 41 频数 8 4 5 a 1 若该组数据的中位数不大于 38，则符合条件的a(a≠0)的取值共有个.
15. 在某中学的一次田径运动会上，参加女子跳高的7名运动员的成绩如下(单位：m)：1.20，1.25，1.10，1.15，1.35，1.30，1.30，则这组数据的中位数是.16. 若一组数据 4，x，5，y，7，9 的平均数是6，众数是5，则这组数据的方差是.17. 某公司欲招聘一名职员．对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试，他们的各项成绩如下表所示，如果将每位应聘者的综合知识、工作经验、语言表达的成绩按5 ：2 ：3的比例计算其总成绩，并录用总成绩最高的应聘者，则被录用的是.项目
应聘者
综合知识
工作经验
语言表达
甲
75
80
80
乙
85
80
70
丙
70
78
70
18. 现有甲、乙两种糖果的单价与千克数如表所示．甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克.
三、解答题（共7题，共78分）
-
19. 某公司为提高服务质量，对其某个部门开展了客户满意度问卷调查，客户满意度以分数呈现，满意度从低到高为1分，2分，3分，4分，5分，共5档公司规定：若客户所评分数的平均数或中位数低于3.5分，则该部门需要对服务质量进行整改．工作人员从收回的问卷中随机抽取了20份，如图是根据这20份问卷中的客户所评分数绘制的统计图．
(1)、求客户所评分数的中位数平均数，并判断该部门]是否需要整改．(2)、监督人员从余下的问卷中又随机抽取了1份，与之前的20份合在一起，重新计算后，发现客户所评分数的平均数大于3.55分，求监督人员抽取的问卷所评分数为几分．与(1)相比，中位数是否发生变化？20. 甲乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如表：命中环数
7
8
9
10
甲命中相应环数的次数
2
2
0
1
乙命中相应环数的次数
1
3
1
0
(1)、计算甲、乙两人的射击成绩的平均数；(2)、若从甲、乙两人射击成绩方差的角度评价两人的射击水平，请通过计算说明：谁的射击成绩更稳定些？21. 为提高学生的数学思维能力，某中学开展“迎元旦数学知识竞赛”，八(1)班、八(2)班各选出5名选手参加竞赛，整理5名选手的竞赛成绩(满分为100分)绘制如图所示的统计图和不完整的统计表．平均数
中位数
众数
八(1)班(分)
87
80
八(2)班(分)
85
(1)、请你把表格补充完整；(2)、结合两班竞赛成绩的平均数中位数和众数，你认为哪个班的竞赛成绩较好；(3)、计算两个班竞赛成绩的方差，并说明哪个班的成绩较为整齐．22. 某校学生会要在甲、乙两位候选人中选择一 人担任文艺部干事，对他们进行了文化水平艺术水平组织能力的测试，根据综合成绩择优录取，他们的各项成绩(单项满分100分)如下表所示：候选人
文化水平
艺术水平
组织能力
甲
80分
87分
82分
乙
80分
96分
76分
(1)、如果把各项成绩的平均数作为综合成绩，应该录取谁？(2)、如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计人综合成绩，应该录取谁？23. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了 5箭，他们的总成绩(单位：环)相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差(见小宇的作业).甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲
9
4
7
4
6
乙
7
5
7
a
7
小宇的作业：
解
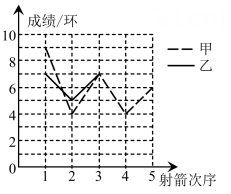(1)、a= ， x₂= ， 甲成绩的众数是 ， 乙成绩的中位数是(2)、请完成图中表示乙成绩变化情况的折线.(3)、①请求出乙成绩的方差，并比较谁的成绩比较稳定.②请你从平均数和方差的角度分析，谁将被选中.
甲、乙两人射箭成绩折线统计图
24. 某校八年级两个班，各选派名学生参加学校举行的“安全知识大赛”预赛，各参赛选手的成绩如下：八（1）班： ， ， ， ， ， ， ， ， ， ；
八（2）班： ， ， ， ， ， ， ， ， ， ．
整理后得到数据分析表如下：
班级
最高分
平均分
中位数
众数
方差
八（1）班
八（2）班
(1)、填空： ， ；(2)、求出表中的值；(3)、你认为哪个班级成绩好？请写出两条你认为该班成绩好的理由．25. 某教育局为了解初中毕业年级学生的体质情况，从某校九年级学生中随机抽取20%的学生进行体质监测．根据《中学生体质健康标准》规定学生体质健康等级标准：90分及以上为优秀；80分～89分为良好；60分～79分为及格；60分以下为不及格，将测试成绩制成如下图表．各等级学生频率分布表
成绩
频数
频率
优秀
16
b
良好
a
0.24
及格
18
0.36
不及格
4
0.08
请根据图表信息回答下列问题：
(1)、表格中的a＝_ ， b＝_ ．(2)、已知“80分～89分”这组的数据如下：81，83，84，85，85，81，80，86，87，88，83，85，则所抽取的这些学生体质监测成绩的中位数是 _ ．(3)、求参加本次体质监测的学生的平均成绩 ．(4)、请估计该校九年级体质监测成绩未达到“良好”等级及以上的学生人数．