（华师大版）2023-2024学年度第二学期八年级数学第十九章 矩形、菱形与正方形 单元测试
试卷更新日期：2024-02-23 类型：单元试卷
一、选择题（每题4分，共48分）
-
1. 下列条件中，能判定四边形是菱形的是（ ）A、两条对角线相等 B、两条对角线互相垂直 C、两条对角线互相垂直平分 D、两条对角线相等且互相垂直2. 如图，在菱形 ABCD中，对角线 AC，BD相交于点O，E 是边AD的中点，连结OE.若菱形ABCD的周长为32，则 OE 的长为 （ ）
A、4 B、6 C、8 D、123. 如图，在菱形 ABCD中，对角线AC，BD相交于点O，下列说法错误的是 （ ）
A、AB∥DC B、∠DAO=∠DCO C、AC⊥BD D、OA=BD4. 如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（ ）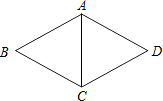
A、5 B、10 C、15 D、205. 如图，菱形ABCD中，∠D＝140°，则∠1的大小是（ ）
A、10° B、20° C、30° D、40°6. 如图，在矩形ABCD中，点A的坐标是（1，0），点C的坐标是（﹣2，4），则BD的长是（ ）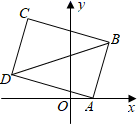
A、 B、5 C、3 D、47. 如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（ ）
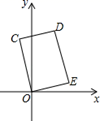A、3 B、 C、 D、48. 如图， 是坐标原点，菱形 的顶点 的坐标为 ，顶点 在 轴的负半轴上，函数 的图象经过顶点 ，则 的值为（ ）
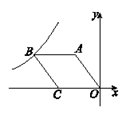A、－12 B、－27 C、－32 D、－369. 如图，在矩形中，对角线 ， 相交于点 ． 下列结论中不一定成立的是（ ）
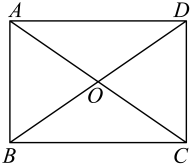A、 B、 C、 D、10. 已知在菱形中， ， ， 则菱形的面积为（ ）
A、160 B、80 C、40 D、9611. 如图，菱形ABCD的边长为5，对角线AC的长为8，延长AB至E，BF平分∠CBE，点G是BF上任意一点，则△ACG的面积为（ ）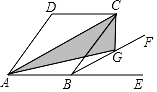
A、6 B、12 C、20 D、2412. 如图，在△ABC中，点D，E，F分别在边BC，AB，CA 上，且 DE∥CA，DF∥BA.有下列说法：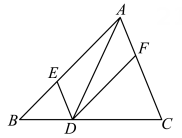
①四边形AEDF 是平行四边形；
②若∠BAC=90°，则四边形AEDF 是矩形；
③若 AD平分∠BAC，则四边形AEDF 是菱形；
④若AD⊥BC，且AB=AC，则四边形AEDF 是正方形.
其中正确的是 （ ）
A、①④ B、②③ C、①②③ D、①②③④二、填空题（每题4分，共24分）
-
13. 已知菱形的周长为20，一条对角线长为8，则菱形的面积为 ．14. 如图，菱形 ABCD的边AB 的垂直平分线交AB 于点 E，交 AC 于 点 F，连 结 DF. 若∠BAD=100°，则∠CDF=°.
15. 如图，长方形ABCD中，AB＝4，AD＝3，折叠纸片使AD边与对角线BD重合，折痕为DG， 则AG=.
16. 如图，菱形的对角线 ， 相交于点 ， 点为边上一动点不与点 ， 重合 ， 于点 ， 于点 ， 若 ， ， 则的最小值为 ．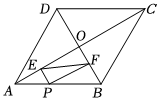
17. 如图，将正方形纸片折叠，为折痕，点落在对角线上的点处，则的度数为 ．
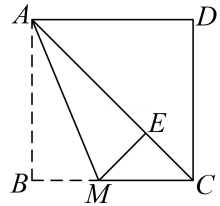18. 如图，直线过正方形ABCD的顶点B，点A、C到直E的距离分别是1和2，则正方形ABCD面积是.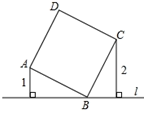
三、解答题（共7题，共78分）
-
19. 如图，在△ABC中，AC=9，AB=12，BC=15，P 为边 BC上一动点，PG⊥AC 于点G，PH⊥AB 于点H.
(1)、求证：四边形 AGPH 是矩形.(2)、在点 P 的运动过程中，GH 的长是否存在最小值? 若存在，请求出最小值；若不存在，请说明理由.20. 如图，在菱形 ABCD中，E，F 分别是边 AD，AB的中点.
(1)、求证：△ABE≌△ADF.(2)、若 求菱形 ABCD的面积.21. 如图，在菱形 ABCD 中，过点 B 作 BM⊥AD 于点 M，BN⊥CD 于点 N，BM，BN 分别交AC 于点 E，F.求证：AE=CF.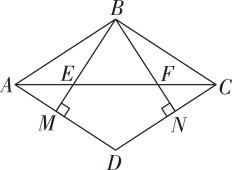
22. 如图，在菱形 ABCD中，对角线AC，BD相交于点O，过点 A 作AE⊥BC于点E，延长 BC 至点 F，使得 CF=BE，连结 DF.
(1)、求证：四边形 AEFD 是矩形.(2)、连结OE，若AB=13，OE=2 ，求 AE 的长.23. 如图，在菱形 ABCD 中，BD为对角线，E 为.BD 上的点.求证：∠DAE=∠DCE.
24. 如图，在平面直角坐标系中，直线y=x+b分别与x轴、轴交于点A，B，且点A的坐标为(4，0)，四边形ABCD是正方形．
(1)、填空：b=.(2)、点M是线段AB上的一个动点(点A，B除外)，试探索在x轴上方是否存在另一个点N，使得以O，B，M，N为顶点的四边形是菱形？若不存在，请说明理由；若存在，请求出点N的坐标(提示：两直线垂直，斜率乘积为-1)25. 如图，在平面直角坐标系中，点A是动点且纵坐标为4，点B是线段OA上的一个动点，过点B作直线MN平行于x轴，设MN分别交射线OA与x轴所成的两个角的平分线于点E，F．
(1)、求证：EB=BF． ．(2)、当为何值时，四边形AEOF是矩形？证明你的结论(3)、是否存在点A，B，使四边形AEOF为正方形？若存在，求出点A与点B的坐标；若不存在，请说明理由．