(华师大版)2023-2024学年度第二学期七年级数学第九章 多边形 单元测试
试卷更新日期:2024-02-23 类型:单元试卷
一、选择题(每题3分,共36分)
-
1. 下列说法错误的是( )
A、三角形的中线、高、角平分线都是线段 B、任意三角形内角和都是180° C、三角形按角可分为锐角三角形、直角三角形和等腰三角形 D、直角三角形两锐角互余2. 下列各图中,作出△ABC的AC边上的高,正确的是( )A、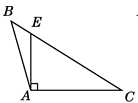 B、
B、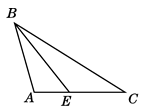 C、
C、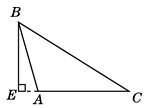 D、
D、 3. 如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G.已知∠1=50°,则∠B的度数为( )
3. 如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G.已知∠1=50°,则∠B的度数为( ) A、20° B、30° C、40° D、50°4. 如图,AB∥DE,∠E=65°,则∠B+∠C=( )
A、20° B、30° C、40° D、50°4. 如图,AB∥DE,∠E=65°,则∠B+∠C=( ) A、135° B、115° C、36° D、65°5. 若一个三角形的两边长分别为 , , 则它的第三边的长可能是( )A、 B、 C、 D、6. 用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )
A、135° B、115° C、36° D、65°5. 若一个三角形的两边长分别为 , , 则它的第三边的长可能是( )A、 B、 C、 D、6. 用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )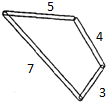 A、6 B、7 C、8 D、97. 若正多边形的一个外角是 , 则该正多边形的内角和为( )A、 B、 C、 D、8. 如图,四边形中, , , 、的平分线相交于点E,则( )
A、6 B、7 C、8 D、97. 若正多边形的一个外角是 , 则该正多边形的内角和为( )A、 B、 C、 D、8. 如图,四边形中, , , 、的平分线相交于点E,则( ) A、 B、 C、 D、9. 只用下列正多边形地砖中的一种,能够铺满地面的是( )A、正十边形 B、正八边形 C、正六边形 D、正五边形10. 下列正多边形的组合中,能够铺满地面的是( )A、正八边形和正三角形 B、正八边形和正方形 C、正八边形和正五边形 D、正六边形和正方形11. 如图,张明同学设计了四种正多边形的瓷砖图案,这四种瓷砖图案中,不能铺满地面的是( )A、
A、 B、 C、 D、9. 只用下列正多边形地砖中的一种,能够铺满地面的是( )A、正十边形 B、正八边形 C、正六边形 D、正五边形10. 下列正多边形的组合中,能够铺满地面的是( )A、正八边形和正三角形 B、正八边形和正方形 C、正八边形和正五边形 D、正六边形和正方形11. 如图,张明同学设计了四种正多边形的瓷砖图案,这四种瓷砖图案中,不能铺满地面的是( )A、 B、
B、 C、
C、 D、
D、 12. 利用边长相等的正三角形和正六边形地砖能够铺满地板,若在每个顶点处有a块正三角形和b块正六边形(ab0),则a+b的值为( )A、4 B、5 C、6 D、7
12. 利用边长相等的正三角形和正六边形地砖能够铺满地板,若在每个顶点处有a块正三角形和b块正六边形(ab0),则a+b的值为( )A、4 B、5 C、6 D、7二、填空题(每题4分,共24分)
-
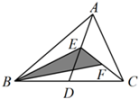
13. 如图,在中,已知点D , E , F分别为边 , , 的中点,且的面积等于 , 则阴影部分图形面积等于 .
 14. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25%,则∠2的度数为
14. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25%,则∠2的度数为 15. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长等于 .16. 在四边形中, , , 则的度数为.17. 若n边形的内角和与外角和相等,则n的值为.18. 现有①正方形②正五边形③正六边形④正八边形,其中可以单独密铺的图形是 . (填序号即可)
15. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长等于 .16. 在四边形中, , , 则的度数为.17. 若n边形的内角和与外角和相等,则n的值为.18. 现有①正方形②正五边形③正六边形④正八边形,其中可以单独密铺的图形是 . (填序号即可)三、解答题(共7题,共60分)
-
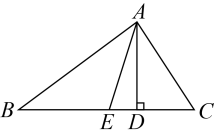
19. 如图中, , 分别是的高和角平分线, , . 求的度数.
 20. 已知,AB∥CD,点F 在 AB上,过点F 引射线FM,交 CD 于点G,E 为射线 FG 上一点,连结DE,AE.
20. 已知,AB∥CD,点F 在 AB上,过点F 引射线FM,交 CD 于点G,E 为射线 FG 上一点,连结DE,AE. (1)、如图 1,若∠EAF=30°,∠EDG=40°,求∠AED的度数.(2)、如图2,当点E在射线GM 上时,CD与AE 相交于点 H,则∠AED,∠EAF,∠EDG 之间满足怎样的关系? 请说明理由.(3)、如图3,在(2)的条件下,I是∠EDC平分线上一点,连结 DI 交 AE 于点 K,连结 AI,若∠EAI:∠BAI= 1 : 2,∠AED=22°,∠I =20°,求∠EKD的度数21. 一个多边形的内角和比它的外角和的4倍多180°,求这个多边形的边数和它的内角和.22. 在正多边形中,某一个外角等于某一个内角的 ,求这个正多边形的边数.23. ①一个多边形的内角和等于它的外角和的3倍,则它是几边形?
(1)、如图 1,若∠EAF=30°,∠EDG=40°,求∠AED的度数.(2)、如图2,当点E在射线GM 上时,CD与AE 相交于点 H,则∠AED,∠EAF,∠EDG 之间满足怎样的关系? 请说明理由.(3)、如图3,在(2)的条件下,I是∠EDC平分线上一点,连结 DI 交 AE 于点 K,连结 AI,若∠EAI:∠BAI= 1 : 2,∠AED=22°,∠I =20°,求∠EKD的度数21. 一个多边形的内角和比它的外角和的4倍多180°,求这个多边形的边数和它的内角和.22. 在正多边形中,某一个外角等于某一个内角的 ,求这个正多边形的边数.23. ①一个多边形的内角和等于它的外角和的3倍,则它是几边形?②某学校想用地砖铺地,学校已准备了一批完全相同的正n边形[n为(1)中的所求值],如果单独用这种地砖能密铺吗?
③如果不能,请你自己只选用一种同(2)边长相同的正方形地砖搭配能密铺吗?如果能,请你画出一片密铺的示意图.

