高中数学三轮复习（直击痛点）：专题21解析几何中的定点与定值问题

试卷更新日期：2024-02-23 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 已知直线 $l_{1} ： 2 x - m y + 3 m = 0$ 与直线 $l_{2} ： m x + 2 y - 4 m + 2 = 0$ 分别过定点A ， B ，且交于点P ，则 $△ P A B$ 面积的最大值是（）

A、5 B、8 C、10 D、16

查看试题解析
2. 由伦敦著名建筑事务所SteynStudio设计的南非双曲线大教堂惊艳世界，该建筑是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线 $\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1$ $(a > 0 ， b > 0)$ 下支的一部分，且此双曲线的下焦点到渐近线的距离为2，离心率为2，则该双曲线的方程为（）

A、 $\frac{y^{2}}{12} - \frac{x^{2}}{4} = 1$ B、 $\frac{3 y^{2}}{4} - \frac{x^{2}}{4} = 1$ C、 $\frac{x^{2}}{4} - \frac{y^{2}}{4} = 1$ D、 $\frac{y^{2}}{16} - \frac{x^{2}}{4} = 1$

查看试题解析
3. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 ， (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2} ， O$ 为坐标原点，P是双曲线在第一象限上的点， $\vec{| P F_{1} |} = 2 \vec{| P F_{2} |} = 2 m ， (m > 0) ， \vec{P F_{1}} \cdot \vec{P F_{2}} = m^{2}$ ，则双曲线C的渐近线方程为（）

A、 $y = \pm \frac{1}{2} x$ B、 $y = \pm \frac{\sqrt{2}}{2} x$ C、 $y = \pm x$ D、 $y = \pm \sqrt{2} x$

查看试题解析
4. 已知直线 $l$ 的一个方向向量为 $(2 ， - 3)$ ，且经过点 $(3 ， 1)$ ，则 $l$ 的方程为（）

A、 $3 x + 2 y - 3 = 0$ B、 $3 x + 2 y - 11 = 0$ C、 $2 x - 3 y - 1 = 0$ D、 $3 x + 2 y + 3 = 0$

查看试题解析
5. 知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =$ 1（a＞b＞0）的左、右焦点分别是F₁、F₂ ，直线y＝kx与椭圆C交于A ， B两点，|AF₁|＝3|BF₁|，且∠F₁AF₂＝60°，则椭圆C的离心率是（　　）

A、 $\frac{7}{16}$ B、 $\frac{\sqrt{7}}{4}$ C、 $\frac{9}{16}$ D、 $\frac{3}{4}$

查看试题解析
6. 已知 $P$ 为双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 上一点， $A (0 ， b) ， B$ 为 $C$ 的右焦点，若 $\vec{A P} = \vec{P B}$ ，则 $C$ 的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
7. 已知两点 $A (- 1 ， 5) ， B (0 ， 0)$ ，若直线 $l ： (k + 1) x - (2 k - 2) y + 2 k - 6 = 0$ 与线段 $A B$ 有公共点，则直线 $l$ 倾斜角的取值范围为（）

A、 $[- 1 ， 1]$ B、 $[\frac{π}{4} ， \frac{3 π}{4}]$ C、 $[\frac{π}{4} ， \frac{π}{2}) \cup (\frac{π}{2} ， \frac{3 π}{4}]$ D、 $[0 ， \frac{π}{4}] \cup [\frac{3 π}{4} ， π)$

查看试题解析
8. 已知椭圆的方程为 $\frac{x^{2}}{a^{2}} + y^{2} = 1 (a > 1)$ ，上顶点为 $A$ ，左顶点为 $B$ ，设 $P$ 为椭圆上一点，则 $Δ P A B$ 面积的最大值为 $\sqrt{2} + 1$ .若已知 $M (- \sqrt{3} ， 0) ， N (\sqrt{3} ， 0)$ ，点 $Q$ 为椭圆上任意一点，则 $\frac{1}{| Q N |} + \frac{4}{| Q M |}$ 的最小值为（）

A、2 B、 $3 + 2 \sqrt{2}$ C、3 D、 $\frac{9}{4}$

查看试题解析

二、多项选择题

9. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{4} = 1 (a > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，过 $F_{2}$ 作直线 $y = \frac{2}{a} x$ 的垂线，垂足为 $P$ ，且与 $C$ 的右支交于点 $Q$ ， $O$ 为坐标原点，且 $∠ F_{1} P O = \frac{π}{6}$ ，则（）

A、 $| O P | = \sqrt{3}$ B、 $C$ 的离心率为 $\frac{\sqrt{13}}{3}$ C、 $s i n ∠ P F_{1} F_{2} = \frac{\sqrt{21}}{14}$ D、 $S_{△ O F_{2} Q} = 4 \sqrt{3} - 6$

查看试题解析

三、填空题

10. 点 $A$ 是圆 $x^{2} + y^{2} = 4$ 上的一个动点，点 $B (0 ， 4)$ ，当点 $A$ 在圆上运动时，线段 $A B$ 的中点 $P$ 的轨迹方程为.

查看试题解析
11. 阿基米德是古希腊著名的数学家、物理学家，他利用“通近法”得到椭圆的面积，除以圆周率 $π$ 等于椭圆的长半轴长与短半轴长的乘积.已知面积为 $6 \sqrt{2} π$ 的椭圆，以 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ ( $a > b > 0$ )的左焦点为 $F (- 1 ， 0)$ ， P为椭圆上任意一点，点Q的坐标为 $(1 ， 1)$ ，则 $| P Q | + | P F |$ 的最大值为.

查看试题解析
12. 已知圆 $O ： x^{2} + y^{2} = 4$ ，过点 $A (1 ， 1)$ 的直线l与圆O交于P、Q两点，则 $| P Q |$ 的最小值等于．

查看试题解析
13. 已知直线 $y = x - 2$ 与双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ $(a > 0 ， b > 0)$ 的两条渐近线分别交于点 $A$ ， $B$ （不重合）线段 $A B$ 的垂直平分线过点 $(4 ， 0)$ ，则双曲线 $C$ 的离心率为．

查看试题解析
14. 已知抛物线 $y^{2} = 4 x$ 上存在两点 $A ， B$ （ $A ， B$ 异于坐标原点 $O$ ），使得 $∠ A O B = 90 °$ ，直线AB与x轴交于M点，将直线AB绕着M点逆时针旋转 $90 °$ 与该抛物线交于C ， D两点，则四边形ACBD面积的最小值为.

查看试题解析
15. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦点为 $F_{1}$ ， $F_{2}$ ， P是椭圆上一点，且 $∠ F_{1} P F_{2} = \frac{π}{3}$ ，若 $△ F_{1} P F_{2}$ 的外接圆和内切圆的半径分别为R ， r ，当 $R = 3 r$ 时，椭圆的离心率为．

查看试题解析
16. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点为 $F$ ，直线 $l ： 3 x + 4 y = 0$ 与 $C$ 相交于 $A ， B$ 两点，若 $| A B | = 2 | O F |$ （ $O$ 为坐标原点），则 $C$ 的离心率为．

查看试题解析
17. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右顶点分别为 $A ， B ， Q$ 为椭圆上异于 $A ， B$ 的任意一点.过右焦点作 $x$ 轴的垂线与椭圆在第一象限交于点 $P$ ，连接 $A P$ 并延长交直线 $x = \frac{a^{2}}{c}$ 于点 $C$ ，若 $\vec{A P} = λ \vec{P C} (1 ⩽ λ ⩽ 2)$ ，且 $t a n ∠ Q A B \cdot t a n ∠ Q B A < \frac{2}{3}$ ，则椭圆离心率的取值范围是.

查看试题解析

四、解答题

18. 过点 $P (0 ， 2)$ 作斜率为 $k (k > 0)$ 的直线 $l$ 与抛物线 $C$ ： $x^{2} = 2 p y (p > 0)$ 交于 $A$ ， $B$ 两点， $O$ 为坐标原点，当 $k = 1$ 时， $\vec{O A} \cdot \vec{O B} = - 4$ .

(1)、求抛物线 $C$ 的方程；

(2)、过点 $A$ 作 $A D ⊥ A B$ 交 $y$ 轴于点 $D$ ，过点 $B$ 作 $B E ⊥ A B$ 交 $y$ 轴于点 $E$ ，记 $△ P A D$ ， $△ P B E$ 面积分别为 $S_{1}$ ， $S_{2}$ ，求当 $S_{1} + S_{2}$ 取得最小值时直线 $l$ 的方程.

查看试题解析
19. 在平面直角坐标系 $x O y$ 中，已知点 $F_{1} (- 6 ， 0)$ 、 $F_{2} (6 ， 0)$ ， $△ M F_{1} F_{2}$ 的内切圆与直线 $F_{1} F_{2}$ 相切于点 $D (4 ， 0)$ ，记点M的轨迹为C.

(1)、求C的方程；

(2)、设点T在直线 $x = 2$ 上，过T的两条直线分别交C于A、B两点和P ， Q两点，连接 $B P ， A Q$ .若直线 $A B$ 的斜率与直线 $P Q$ 的斜率之和为0，试比较 $c o s ∠ B A Q$ 与 $c o s ∠ B P Q$ 的大小.

查看试题解析
20. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率e满足 $2 e^{2} - 3 \sqrt{2} e + 2 = 0$ ，右顶点为A，上顶点为B，点C(0，－2)，过点C作一条与y轴不重合的直线l ，直线l交椭圆E于P，Q两点，直线BP，BQ分别交x轴于点M，N；当直线l经过点A时，l的斜率为 $\sqrt{2}$ ．

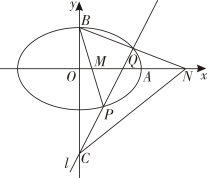(1)、求椭圆E的方程；

(2)、证明： $S_{Δ B O M} \cdot S_{Δ B C N}$ 为定值．

查看试题解析
21. 已知双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ＞ 0 ， b ＞ 0)$ 的左右焦点分别为F₁ ， F₂ ， F₁到其中一条渐近线的距离为1，过F₁且垂直于x轴的直线交双曲线于A ， B ，且|AB|＝1．

(1)、求E的方程；

(2)、过Q（4，0）的直线l交曲线E于M ， N两点，若|MN|＝4，求直线l的方程．

查看试题解析
22. 在平面直角坐标系中，已知点 $F_{1} (- 2 ， 0)$ ， $F_{2} (2 ， 0)$ ，点 $P$ 满足 $| P F_{1} | + | P F_{2} | = 2 \sqrt{6}$ . 记 $P$ 的轨迹为 $C$ .

(1)、求 $C$ 的方程；

(2)、已知点 $A (\sqrt{3} ， 1)$ ，设点 $M$ ， $N$ 在 $C$ 上，且直线 $M N$ 不与 $x$ 轴垂直，记 $k_{1}$ ， $k_{2}$ 分别为直线 $A M$ ， $A N$ 的斜率.
（ⅰ）对于给定的数值 $λ$ （ $λ \in R$ 且 $λ \neq \frac{1}{3}$ ），若 $k_{1} k_{2} = λ$ ，证明：直线 $M N$ 经过定点；
（ⅱ）记（ⅰ）中的定点为 $Q$ ，求点 $Q$ 的轨迹方程.

查看试题解析
23. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 经过点 $A (0 ， 1)$ ，且离心率为 $\frac{\sqrt{6}}{3}$ .

(1)、求椭圆 $C$ 的方程；

(2)、 $M ， N$ 是椭圆 $C$ 上的两个动点（ $M ， N$ 与点 $A$ 不重合），直线 $A M ， A N$ 的斜率之和为4，作 $A H ⊥ M N$ 于 $H$ .是否存在定点 $P$ ，使得 $| P H |$ 为定值.若存在，求出定点 $P$ 的坐标及 $| P H |$ 的值；若不存在，请说明理由.

查看试题解析