浙江省温州市2023-2024学年高二上学期数学期末教学质量统一监测试卷（A卷）

试卷更新日期：2024-02-23 类型：期末考试

进入出卷网下载

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知直线方程 $x + y + 1 = 0$ ，则倾斜角为（）

A、45° B、60° C、120° D、135°

查看试题解析
2. 在空间四边形ABCD中，点M ， G分别是BC和CD的中点，则 $\vec{A B} + \frac{1}{2} (\vec{B D} + \vec{B C}) =$ （）

A、 $\vec{A D}$ B、 $\vec{G A}$ C、 $\vec{A G}$ D、 $\vec{M G}$

查看试题解析
3. 已知函数f（x）满足 $f (x) = f^{'} (\frac{π}{3}) s i n x - c o s x$ ，则 $f^{'} (\frac{π}{3})$ 的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $- \sqrt{3}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
4. 已知 $S_{n}$ 为等比数列 ${a_{n}}$ 的前n项和， $S_{n} = m \cdot 2^{n} - 1$ ，则 $a_{4} =$ （）

A、2 B、4 C、8 D、16

查看试题解析
5. 已知圆锥有一个内接圆柱，当圆柱的侧面积最大时，圆柱与圆锥的高之比为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
6. 传说古希腊毕达哥拉斯学派的数学家用沙粒或小石子来研究数．他们根据沙粒或小石头所排列的形状把数分成许多类，如图的1，5，12，22称为五边形数，若五边形数所构成的数列记作 ${a_{n}}$ ，下列不是数列 ${a_{n}}$ 的项的是（）

A、35 B、70 C、145 D、170

查看试题解析
7. 已知F为椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左焦点，过点F的直线l交椭圆于A ， B两点， $| A F | \cdot | B F | = \frac{12}{5}$ ，则直线AB的斜率为（）

A、 $\pm 2$ B、 $\pm \sqrt{3}$ C、 $\pm \sqrt{2}$ D、 $\pm 1$

查看试题解析
8. 若函数 $f (x) = a^{x} + b^{x}$ 在 $(0 ， + ∞)$ 上单调递增，则a和b的可能取值为（）

A、 $a = l n 1.1$ ， $b = 10$ B、 $a = l n 11$ ， $b = 0.1$ C、 $a = e^{0.2}$ ， $b = 0.8$ D、 $a = e^{- 0.2}$ ， $b = 1.8$

查看试题解析

二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．

9. 以下选项中的两个圆锥曲线的离心率相等的是（）

A、 $\frac{x^{2}}{4} - \frac{y^{2}}{2} = 1$ 与 $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$ B、 $\frac{x^{2}}{4} - \frac{y^{2}}{2} = 1$ 与 $\frac{y^{2}}{2} - \frac{x^{2}}{4} = 1$ C、 $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$ 与 $\frac{x^{2}}{2} + \frac{y^{2}}{4} = 1$ D、 $y^{2} + 4 x = 0$ 与 $x^{2} + 2 y = 0$

查看试题解析
10. 已知函数 $f (x) = x^{3} + 3 x^{2}$ ，则（）

A、 $f^{'} (- 1) = - 3$ B、f（x）有两个极值点 C、f（x）在区间 $(- 3 ， 3)$ 上既有最大值又有最小值 D、 $f (- \frac{5}{2}) + f (- 1) + f (\frac{1}{2}) = 6$

查看试题解析
11. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{1} < 0$ ， $a_{1} + a_{2} > 0$ ，则下列命题正确的是（）

A、若 ${a_{n}}$ 为等差数列，则数列 ${S_{n}}$ 为递增数列 B、若 ${a_{n}}$ 为等比数列，则数列 ${S_{n}}$ 为递增数列 C、若 ${a_{n}}$ 为等差数列，则数列 ${| a_{n} |}$ 为递增数列 D、若 ${a_{n}}$ 为等比数列，则数列 ${| a_{n} |}$ 为递增数列

查看试题解析
12. 已知在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} = 4$ ， $A C = B C = 2$ ， $A C ⊥ B C$ ，点E ， F ， T分别为棱 $A_{1} A$ ， $C_{1} C$ ， AB上的动点（不含端点），点M为棱BC的中点，且 $A_{1} E = F C = \sqrt{2} B T$ ，则（）

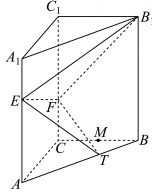A、 $A_{1} B ∥$ 平面EFT B、 $M \in$ 平面EFT C、点A到平面EFT距离的最大值为 $\frac{\sqrt{14}}{2}$ D、平面 $B_{1} E F$ 与平面ABC所成角正弦值的最小值为 $\frac{\sqrt{2}}{2}$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分．

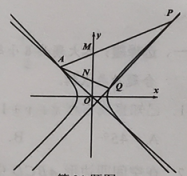
13. 等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，已知 $3 S_{3} = S_{2} + 2 S_{4}$ ，且 $a_{4} = 1$ ，则公差 $d =$ ．

查看试题解析
14. 已知圆 $C_{1}$ ： $x^{2} + y^{2} - 8 x + 7 = 0$ 和圆 $C_{2}$ ： $x^{2} + y^{2} + 6 y + m = 0$ 外离，则整数m的一个取值可以是．

查看试题解析
15. 两个正方形ABCD ， ABEF的边长都是1，且它们所在的平面互相垂直，M和N分别是对角线AC和BF上的动点，则MN的最小值为．

查看试题解析
16. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， l： $y = \sqrt{3} x$ 是C的一条渐近线，P是C第一象限上的点，直线 $P F_{1}$ 与l交于点Q ， $Q F_{1} ⊥ Q F_{2}$ ，则 $t a n \frac{∠ F_{1} P F_{2}}{2} =$ ．

查看试题解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明．证明过程或演算步骤．

17. 如图，四棱锥 $P - A B C D$ 的底面是边长为1的菱形， $∠ A B C = \frac{2}{3} π$ ， $P D ⊥$ 平面ABCD ， $P D = 1$ ， M为PB的中点．

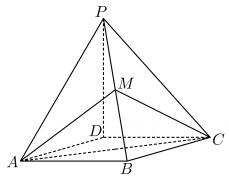(1)、求证：平面 $M A C ⊥$ 平面PDB；

(2)、求CP与平面MAC所成角的正弦值．

查看试题解析
18. 已知圆C截y轴所得弦长为2，被x轴分成的两段圆弧的弧长比为3：1，且圆心C到直线 $x - 2 y = 0$ 的距离为 $\frac{\sqrt{5}}{5}$ ，求圆C的方程．

查看试题解析
19. 已知数列 ${a_{n}}$ 满足 $a_{n + 1} = \frac{a_{n}}{a_{n} + 1}$ ， $a_{1} = \frac{1}{2}$ ．

(1)、求证：数列 ${\frac{1}{a_{n}}}$ 为等差数列；

(2)、设数列 ${a_{n}}$ 前n项和为 $S_{n}$ ，且 $S_{2 n} - S_{n} > k$ 对任意的 $n \in N^{*}$ 恒成立，求k的取值范围．

查看试题解析
20. 已知函数 $f (x) = l n x - a x$ ．

(1)、讨论f（x）的单调性；

(2)、求证：当 $a > 0$ 时， $f (x) + 4 < \frac{4}{\sqrt{a}}$ ．

查看试题解析
21. 已知点 $A (- \sqrt{5} ， 2)$ 在双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{a^{2}} = 1$ 上，

(1)、求C的方程；

(2)、如图，若直线l垂直于直线OA ，且与C的右支交于P、Q两点，直线AP、AQ与y轴的交点分别为点M、N ，记四边形MPQN与三角形APQ的面积分别为 $S_{1}$ 与 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的取值范围．

查看试题解析
22. 设函数 $f (x) = (x - 2) e^{a x}$ ．

(1)、若曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程为 $y - 3 x + b = 0$ ，求a ， b的值；

(2)、若当 $x > 0$ 时，恒有 $f (x) > - x - 2$ ，求实数a的取值范围；

(3)、设 $n \in N^{*}$ 时，求证： $\frac{3}{1^{2} + 2^{2}} + \frac{5}{2^{2} + 3^{2}} + \cdot \cdot \cdot + \frac{2 n + 1}{n^{2} + {(n + 1)}^{2}} < l n (n + 1)$ ．

查看试题解析