广东省深圳市33校联考2024年九年级数学质量检测(2月)
试卷更新日期:2024-02-23 类型:中考模拟
一、选择题:(每小题只有一个正确选项,每小题3分,共计30分)
-
1. “斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
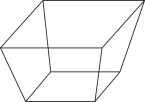 A、
A、 B、
B、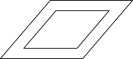 C、
C、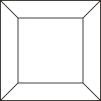 D、
D、 2. 如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
2. 如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( ) A、 B、 C、 D、3. 将抛物线 先向左平移 2 个单位, 再向下平移 3 个单位后, 抛物线的解析式为 ( )A、 B、 C、 D、4. 如图, 已知 , 则 CE的长为 ( )
A、 B、 C、 D、3. 将抛物线 先向左平移 2 个单位, 再向下平移 3 个单位后, 抛物线的解析式为 ( )A、 B、 C、 D、4. 如图, 已知 , 则 CE的长为 ( ) A、 B、 C、6 D、5. 如图, 在矩形 ABCD 中, , 对角线AC与BD相交于点 , A E 垂直平分OB于点 E, 则 BC的长为( )
A、 B、 C、6 D、5. 如图, 在矩形 ABCD 中, , 对角线AC与BD相交于点 , A E 垂直平分OB于点 E, 则 BC的长为( ) A、 B、 C、4 D、26. 关于 x 的方程 x(x-1)=3(x-1),下列解法完全正确的是 ( )
A、 B、 C、4 D、26. 关于 x 的方程 x(x-1)=3(x-1),下列解法完全正确的是 ( )甲 乙 丙 丁 两边同时除以(x-1)得到x=3. 移项得x(x-1)+3(x-1)=0,
∴(x-1)(x+3)=0,
∴x-1=0或x+3=0,
∴x1=1,x2=-3.整理得x2-4x=-3,
∵a=1,b=-4,c=-3,
∴Δ=b2-4ac=28,
∴x= ,
∴x1= , x2= .整理得x2-4x=-3,
配方得x2-4x+4=1,
∴(x-2)2=1,
∴x-2=±1,
∴x1=1,x2=3.A、甲 B、乙 C、丙 D、丁7. 如图,安装路灯AB的路面CD比种植树木的地面PQ高CP=1.2 m,在路灯的照射下,路基CP留在地面上的影长EP为0.4 m,通过测量知道BC的距离为1.5 m,则路灯AB的高度是( ) A、3 m B、3.6 m C、4.5 m D、6 m8. 二次函数的图象如图所示,则一次函数和反比例函数在同一直角坐标系中的图象可能是( )
A、3 m B、3.6 m C、4.5 m D、6 m8. 二次函数的图象如图所示,则一次函数和反比例函数在同一直角坐标系中的图象可能是( )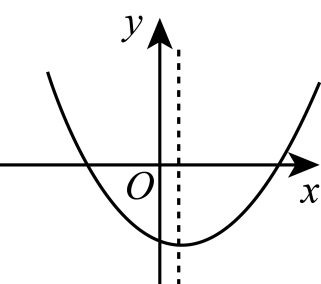 A、
A、 B、
B、 C、
C、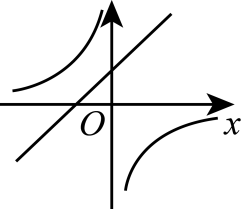 D、
D、 9. 《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹裘的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹杆的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为x尺,则可列方程为( )A、 B、 C、 D、10. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )
9. 《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹裘的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹杆的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为x尺,则可列方程为( )A、 B、 C、 D、10. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )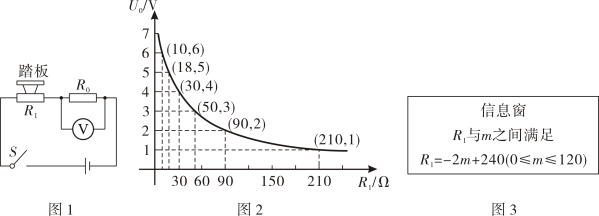 A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是
A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是二、填空题:(每小题 3 分, 共计 15 分)
-
11. 已知 , 则 .12. 为了估计抛掷同一枚瓶盖落地后凸面向上的概率, 小明做了大量重复试验. 经过统计得到凸面向上的次数为 450 次, 凸面向下的次数为 550 次, 由此可估计抛郑瓶盖落地后凸面向上的概率约为.13. 如图,原点是和的位似中心,点与点是对应点,的面积是3,则的面积是 .
 14. 如图, 4 个小正方形拼成 “ ” 型模具, 其中三个顶点在正坐标轴上, 顶点 在反比例函数 的图象上, 若 , 则 .
14. 如图, 4 个小正方形拼成 “ ” 型模具, 其中三个顶点在正坐标轴上, 顶点 在反比例函数 的图象上, 若 , 则 .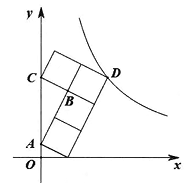 15. 如图, 在 中, 是 B C 边上一点且满足 是 A C 边上一点且满足 , 连接 B E 交 A D 于点 , 则 .
15. 如图, 在 中, 是 B C 边上一点且满足 是 A C 边上一点且满足 , 连接 B E 交 A D 于点 , 则 .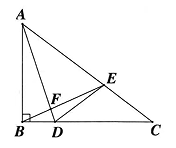
三、解答题: (共 7 题, 共 55 分)
-
16. 计算:2cos45° tan30°cos30°+sin260°.17. 为建设美好公园社区, 增强民众生活幸福感, 如图 1, 某社区服务中心在文化活动室墙外安装遮阳篷, 便于社区居民休想. 在如图 2 的侧面示意图中, 遮阳篷靠墙端离地高记为 B C, 遮阳篷 A B 长为 5 米, 与水平面的夹角为 .
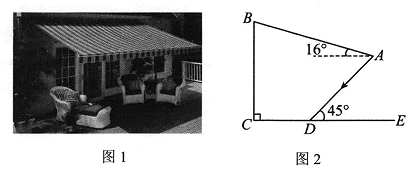 (1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )18. 某超市在元旦节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式:
(1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )18. 某超市在元旦节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式:方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠,指针指向其它区域无优惠;
方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受9折优惠,其它情况无优惠.
(备注:①转盘甲中,指针指向每个区域的可能性相同;转盘乙中,B、C区域的圆心角均为90°;②若指针指向分界线,则重新转动转盘.)
 (1)、若顾客选择方式一,则享受9折优惠的概率为;(2)、两种方式中,哪一种让顾客获得9折优惠的可能性大?请用树状图或列表法说明理由.19. 社区利用一块矩形空地建了一个小型停车场,其布局如图所示.已知 , , 阴影部分设计为停车位,要铺花砖,其余部分均为宽度为米的道路.已知铺花砖的面积为 .
(1)、若顾客选择方式一,则享受9折优惠的概率为;(2)、两种方式中,哪一种让顾客获得9折优惠的可能性大?请用树状图或列表法说明理由.19. 社区利用一块矩形空地建了一个小型停车场,其布局如图所示.已知 , , 阴影部分设计为停车位,要铺花砖,其余部分均为宽度为米的道路.已知铺花砖的面积为 . (1)、求道路的宽是多少米?(2)、该停车场共有车位个,据调查分析,当每个车位的月租金为元时;可全部租出;若每个车位的月租金每上涨元,就会少租出个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为元。20. 如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 .
(1)、求道路的宽是多少米?(2)、该停车场共有车位个,据调查分析,当每个车位的月租金为元时;可全部租出;若每个车位的月租金每上涨元,就会少租出个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为元。20. 如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 . (1)、求证:四边形ADBE是菱形;(2)、连接OC,若四边形ADBE的周长为20, , 求 O C 的长21. 综合与应用
(1)、求证:四边形ADBE是菱形;(2)、连接OC,若四边形ADBE的周长为20, , 求 O C 的长21. 综合与应用如果将运动员的身体看作一点,则他在跳水过程中运动的轨迹可以看作为抛物线的一部分.建立如图2所示的平面直角坐标系xOy,运动员从点A(0,10)起跳,从起跳到入水的过程中,运动员的竖直高度y (m)与水平距离x (m)满足二次函数的关系.
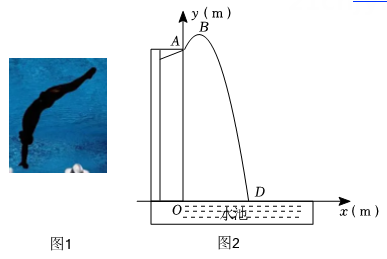 (1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:
(1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:水平距离x(m)
0 1
1.5
竖直高度y(m)
10
10
6.25
根据上述数据,求出y关于x的关系式;
(2)、在(1)的这次训练中,求运动员甲从起点A到入水点的水平距离OD的长;(3)、信息1:记运动员甲起跳后达到最高点B到水面的高度为k(m),从到达到最高点B开始计时,则他到水面的距离h (m)与时间t (s)之间满足h=-5t2+k .信息2:已知运动员甲在达到最高点后需要1.6s的时间才能完成极具难度的270C 动作.
问题解决:
①请通过计算说明,在(1)的这次训练中,运动员甲能否成功完成此动作?
②运动员甲进行第二次跳水训练,此时他的竖直高度y(m)与水平距离x (m)的关系为y =ax2-ax+10(a<0),若选手在达到最高点后要顺利完成270C 动作,则a的取值范围是 ▲ .
22. 综合与实践在一次综合实践活动课上,王老师给每位同学各发了一张正方形纸片,请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点.


【操作探究】
“乘风”小组的同学经过一番思考和讨论交流后,进行了如下操作:
第1步:如图1所示,先将正方形纸片ABCD对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:将BC边沿CE翻折到GC的位置;
第3步:延长EG交AD于点H,则点H为AD边的三等分点.
证明过程如下:连接CH,
∵正方形ABCD沿CE折叠,
∴∠D=∠B=∠CGH=90°, ① ,
又∵CH=CH
∴△CGH≌△CDH,
∴GH=DH.
由题意可知E是AB的中点,设AB=6(个单位),DH=x,则AE=BE=EG=3,
在Rt△AEH中,可列方程: ② , (方程不要求化简)解得:DH= ③ , 即H是AD边的三等分点.
“破浪”小组是这样操作的:
第1步:如图2所示,先将正方形纸片对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:再将正方形纸片对折,使点B与点D重合,再展开铺平,折痕为AC,沿DE翻折得折痕DE交AC于点G;
第3步:过点G折叠正方形纸片ABCD,使折痕MNIIAD.
【过程思考】
(1)、“乘风”小组的证明过程中,三个空的所填的内容分别是: ① , ②: , ③: ;(2)、结合“破浪”小组操作过程,判断点M是否为AB边的三等分点,并证明你的结论;(3)、【拓展提升】如图3,在菱形ABCD中,AB=5,BD=6,E是BD上的一个三等分点,记点D关于AE的对称点为D',射线ED'与菱形ABCD 的边交于点F,请直接写出D'F的长.