2024年人教版中考数学二轮复习专题8 一元二次方程（选填专练）

试卷更新日期：2024-02-23 类型：二轮复习

进入出卷网下载

一、选择题

1. 下列方程是一元二次方程的是（）

A、3x²+y＝2 B、x²﹣ $\frac{1}{x}$ +1＝0 C、x²﹣5x＝3 D、x﹣3y+1＝0

查看试题解析
2. 方程2x²﹣ax+7＝0，有一根是 $\frac{1}{2}$ ，则另一根为（　　）

A、7 B、7.5 C、﹣7 D、15

查看试题解析
3. 若a是关于x的方程3x²﹣x﹣1=0的一个根，则2021﹣6a²＋2a的值是（）

A、2023 B、2022 C、2020 D、2019

查看试题解析
4. 方程. $x^{2} + 4 x + 3 = 0$ 的两个根为（）

A、 $x_{1} - 1 ， x_{2} = 3$ B、 $. x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 1 ， x_{2} = - 3$ D、 $x_{1} = - 1 ， x_{2} = - 3$

查看试题解析
5. 用配方法解一元二次方程 $x^{2} - 6 x + 8 = 0$ ，配方后得到的方程是（）

A、 ${(x + 6)}^{2} = 28$ B、 ${(x - 6)}^{2} = 28$ C、 ${(x + 3)}^{2} = 1$ D、 ${(x - 3)}^{2} = 1$

查看试题解析
6. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛(每支队伍与其他队伍比赛一场)，单循环比赛共进行了45场，参加比赛的队伍有（）

A、7支 B、8支 C、9支 D、10支

查看试题解析
7. 某地2020年人均可支配收入为2.36万元，2022年达到2.7万元.若2020年至2022年间每年人均可支配收入的增长率都为x，则下面所列方程正确的是（）

A、 $2.7 {(1 + x)}^{2} = 2.36$ B、 $2.36 {(1 + x)}^{2} = 2.7$ C、 $2.7 {(1 - x)}^{2} = 2.36$ D、 $2.36 {(1 - x)}^{2} = 2.7$

查看试题解析
8. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
9. 以 $3$ 和 $4$ 为根的一元二次方程是（）

A、 $x^{2} - 7 x + 12 = 0$ B、 $x^{2} + 7 x + 12 = 0$ C、 $x^{2} + 7 x - 12 = 0$ D、 $x^{2} - 7 x - 12 = 0$

查看试题解析
10. 用因式分解法解下列方程，变形正确的是（）

A、(3x-3)(3x-4)=0，于是3x-3=0或3x-4=0 B、(x+3)(x-1)=1，于是x+3=1或x-1=1 C、(x-2)(x-3)=6，于是x-2=2或x-3=3 D、x(x+2)=0，于是x+2=0

查看试题解析
11. 关于 $x$ 的一元二次方程 $x^{2} + 2 x - 2 t + 3 = 0$ 的两个实数根分别是 $m ， n$ ，则 $(m - t) (n^{2} + 3)$ 的最大值是（）

A、 $- 10$ B、 $- 8$ C、 $- 6$ D、 $- 2$

查看试题解析
12. 将二次函数y＝﹣x²+2x+3的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示.当直线y＝x+b与新函数的图象恰有3个公共点时，b的值为（）

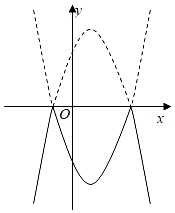A、 $- \frac{21}{4}$ 或﹣3 B、 $- \frac{13}{4}$ 或﹣3 C、 $\frac{21}{4}$ 或﹣3 D、 $\frac{13}{4}$ 或﹣3

查看试题解析
13. 如图，M是△ABC三条角平分线的交点，过M作DE⊥AM ，分别交AB、AC于D ， E两点，设BD=a ， DE=b ， CE=c ，关于x的方程 $a x^{2} + b x + c = 0$ （）

A、一定有两个相等实根 B、一定有两个不相等实根 C、有两个实根，但无法确定是否相等 D、无实根

查看试题解析
14. 将抛物线y＝x²+x﹣6位于y轴左侧的部分沿x轴翻折，其余部分不变，翻折得到的图象和原来不变的部分构成一个新图象，若直线 $y = \frac{1}{2} x + t$ 与新图象有且只有2个公共点，则t的取值范围是（）

A、﹣6<t≤6 B、﹣6<t<6 C、 $t = \frac{97}{16}$ 或﹣6≤t<6 D、 $t = \frac{105}{16}$ 或﹣6≤t≤6

查看试题解析
15. 对于题目“如图，纸片四边形 $A B C D$ ， $A B ⊥ A D ， A B / / B C ， A B = B C = 4 ， A D = 2$ ，点 $E$ 是 $B C$ 上一个动点，过点 $E$ 作直线 $E F ⊥ B C$ ，交AD（或其延长线）于点 $F$ ，以 $E F$ 为折线，将四边形 $A B C D$ 折叠，若重叠的部分的面积为4，确定满足条件的所有 $B E$ 的长”，甲的结果是： $B E = 1$ ，乙的结果是： $B E = 2$ ，则（）

A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确

查看试题解析
16. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴的一个交点为 $A (- 3 ， 0)$ ，与 $y$ 轴交于点 $C$ ，点 $D$ 是抛物线的顶点，对称轴为直线 $x = - 1$ ，其部分图象如图所示，则以下 $4$ 个结论： $① a b c > 0$ ； $② E (x_{1} ， y_{1})$ ， $F (x_{2} ， y_{2})$ 是抛物线 $y = a x^{2} + b x (a \neq 0)$ 上的两个点，若 $x_{1} < x_{2}$ ，且 $x_{1} + x_{2} < - 2$ ，则 $y_{1} < y_{2}$ ； $③$ 在 $x$ 轴上有一动点 $P$ ，当 $P C + P D$ 的值最小时，则点 $P$ 的坐标为 $(- \frac{3}{7} ， 0)$ ； $④$ 若关于 $x$ 的方程 $a x^{2} + b (x - 2) + c = - 4 (a \neq 0)$ 无实数根，则 $b$ 的取值范围是 $b < 1 .$ 其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

17. 若有1个人患了流感，经过2轮传染后共有169人患了流感，则每轮传染中平均1个人传染了个人。

查看试题解析
18. 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排 $28$ 场比赛，比赛组织者应邀请个队参赛．

查看试题解析
19. 《九章算术》中《方田》章有弧田面积计算问题，术曰：以弦乘矢，矢又自乘，并之，二而一．其大意是弧田面积计算公式为：弧田面积 $= \frac{1}{2}$ （弦×矢+矢×矢）．弧田是由圆弧（弧田弧）和以圆弧的端点为端点的线段（弧田弦）围成的平面图形，公式中的“弦”指的是弧田弦的长，“矢”指的是弧田弧所在的圆的半径与圆心到弧田弦的距离之差．现有一弧田，其弧田弦AB等于6米，若用上述弧田面积计算公式算得该弧田的面积为 $\frac{7}{2}$ 平方米，则弧田弧所在的圆的半径为．

查看试题解析
20. 若对任何实数a，关于x的方程x²-2ax-a+2b＝0都有实数根，求实数b的取值范围．

查看试题解析
21. 将二次函数 $y = - x^{2} + 2 x + 3$ 的图象在x轴上方部分沿x轴翻折后，所得新函数的图象如图所示，当直线y=x+b与新函数的图象恰好有3个公共点时，b的值为．

查看试题解析
22. 如图，在平面直角坐标系中，O为坐标原点，四边形 $O A B C$ 是矩形，点A ， C的坐标分别为 $A (9 ， 0)$ ， $C (0 ， 3)$ ，点D以2个单位长度/s的速度从A出发沿A至O方向向终点O运动，点P以1个单位长度/s的速度从C出发沿C至B方向向终点B运动，当 $△ O D P$ 是以 $O P$ 为一腰的等腰三角形时，点P的坐标为．

查看试题解析
23. 对于实数p，q，我们用符号 $m i n {p ， q}$ 表示p，q两数中较小的数，如min ${1 ， 2} =$ $1 ， m i n {- \sqrt{2} ， - \sqrt{3}} = - \sqrt{3}$ .若， $m i n {(x - 1)^{2} ， x^{2}} = 1$ ，则 $x$ 值为.

查看试题解析
24. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，且 $O A = O C .$ 则下列结论： $① b c < 0$ ； $② b^{2} - 4 a c = 0$ ； $③ a c - b + 1 = 0$ ； $④ O A \cdot O B = - \frac{c}{a}$ ；其中正确结论的序号是．

查看试题解析

2024年人教版中考数学二轮复习 专题8 一元二次方程（选填专练）

一、选择题

二、填空题

2024年人教版中考数学二轮复习专题8 一元二次方程（选填专练）