2024年人教版中考数学二轮复习 专题5 一元一次方程
试卷更新日期:2024-02-23 类型:二轮复习
一、选择题
-
1. 若x=2是方程4x+2m﹣14=0的解,则m的值为( )A、10 B、4 C、﹣3 D、32. 若关于 的方程 是一元一次方程,则 的值为( )A、 B、-2 C、2 D、43. 已知 , 下列式子符合等式基本性质的是( )A、 B、 C、 D、4.
《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有个人共同出钱买鸡,则下面所列方程正确的是( )
A、 B、 C、 D、5. 某个体商贩在一次买卖中,同时卖出两件上衣,售价都是135元,若按成本计,其中一件盈利25%,另一件亏本25%,在这次买卖中他( ).A、不赚不赔 B、赚9元 C、赔18元 D、赚18元6. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、7. 下列等式的变形正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么8. 如图,每个圆纸片的面积都是30,圆纸片A与B,B与C,C与A的重叠面积分别为6,8,5,三个圆纸片覆盖的总面积为73,则图中阴影部分的面积为( ) A、54 B、56 C、58 D、699. 如图,平面直角坐标系中,已知点 , , , , 动点从点出发,以每秒个单位的速度按逆时针方向沿四边形的边做环绕运动;另一动点从点出发,以每秒个单位的速度按顺时针方向沿四边形的边做环绕运动,则第次相遇点的坐标是( )
A、54 B、56 C、58 D、699. 如图,平面直角坐标系中,已知点 , , , , 动点从点出发,以每秒个单位的速度按逆时针方向沿四边形的边做环绕运动;另一动点从点出发,以每秒个单位的速度按顺时针方向沿四边形的边做环绕运动,则第次相遇点的坐标是( )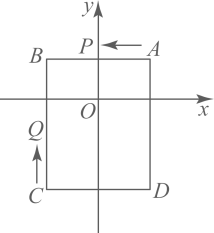 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 在等式的两个方格中分别填入一个数,使这两个数互为相反数且使等式成立,则第一个方格内的数是.11. 由于换季,商场准备对某商品打折出售,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的原售价为元.12. 某工厂生产一批零件,计划20天完成,若每天多生产5个,则16天完成且还多生产8个.设原计划每天生产x个,根据题意可列方程为.13. 把9个数填入3×3方格中,使得每行、每列、每条对角线上的三个数之和都相等,如图是仅可以看到的部分数值,x的值是
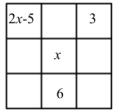 14. 某商场购进一批服装,又恰巧碰到双十一的促销活动,商场决定将这批服装按标价的五折销售,若打折后每件服装可获利润60元,其利润率为;若双十一过后,该商场按这批服装的标价打八折出售,那么获得的利润是元.15. 如图,在长方形ABCD的边上有P , Q两个动点,速度分别为 , , 两个点同时出发,运动过程中,一个点到达终点停止运D动时,另一个点也停止运动,动点P从C点出发,沿折线向终点A运动,动点Q从A点出发,沿射线向终点B运动,运动时间为t秒.若AB=8m, , 当和的面积之和为12平方米时,t的值为 .
14. 某商场购进一批服装,又恰巧碰到双十一的促销活动,商场决定将这批服装按标价的五折销售,若打折后每件服装可获利润60元,其利润率为;若双十一过后,该商场按这批服装的标价打八折出售,那么获得的利润是元.15. 如图,在长方形ABCD的边上有P , Q两个动点,速度分别为 , , 两个点同时出发,运动过程中,一个点到达终点停止运D动时,另一个点也停止运动,动点P从C点出发,沿折线向终点A运动,动点Q从A点出发,沿射线向终点B运动,运动时间为t秒.若AB=8m, , 当和的面积之和为12平方米时,t的值为 .
三、计算题
-
16. 解方程:(1)、2x+3=﹣3x﹣7;(2)、 .17. 解方程:(1)、;(2)、
四、解答题
-
18. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距多少千米.19. 某商场从厂家购进100个整理箱,按进价的1.5倍进行标价.当按标价卖出80个整理箱后,恰逢元旦,剩余的部分以标价的九折出售完毕,所得利润共1880元,求每个整理箱的进价.20. 根据图中情景,解答下列问题:
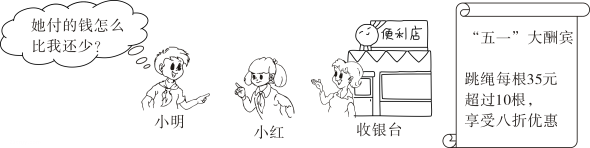 (1)、购买8根跳绳需元;购买12根跳绳需元;(2)、购买m根跳绳需多少元?(请你用含有m的式子表示)(3)、小红比小明多买2根,付款时小红反而比小明少7元,你认为有这种情况有可能吗?请利用方程知识说明理由.21. 已知方程是关于的一元一次方程.(1)、求的值;(2)、若关于的一元一次方程的解与关于的一元一次方程的解互为倒数,求的值.
(1)、购买8根跳绳需元;购买12根跳绳需元;(2)、购买m根跳绳需多少元?(请你用含有m的式子表示)(3)、小红比小明多买2根,付款时小红反而比小明少7元,你认为有这种情况有可能吗?请利用方程知识说明理由.21. 已知方程是关于的一元一次方程.(1)、求的值;(2)、若关于的一元一次方程的解与关于的一元一次方程的解互为倒数,求的值.五、实践探究题
-
22. 在学习“一元一次方程的应用”时.小明和小天在一起讨论下列问题:
某汽车队运送一批援助物资.若每辆车装吨,还剩下吨未装;若每辆车装吨,则最后一辆车还能装吨.这个车队有多少辆车?
(1)、若设这个车队有辆车,根据两种装车方案中援助物资的总量不变,请列出方程并解答.(2)、小明和小天讨论后,觉得也可以设这批援助物资有吨,根据两种装车方案中车辆数不变来列方程,请判断他们的说法是否正确,若正确,按这种方法列出方程并进行解答.六、综合题
-
23. 一列动车匀速行驶,经过某长度为1600 m的大桥用时30 s,桥头一监测仪监测到该动车通过监测仪正前方所用时间为6 s.
 (1)、求该动车的长度;(2)、该动车通过大桥的速度是多少km/h?24. 如图,点A在数轴上表示的数是-9,点D在数轴上表示的数是12,AB=4(单位长度),CD=2 (单位长度)
(1)、求该动车的长度;(2)、该动车通过大桥的速度是多少km/h?24. 如图,点A在数轴上表示的数是-9,点D在数轴上表示的数是12,AB=4(单位长度),CD=2 (单位长度)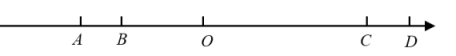 (1)、则点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长= (单位长度);(2)、若点P是线段BC的中点,则P点在数轴上表示的数是:(3)、若点Q是坐标轴上的点,且QC=2QB,则Q点在数轴上表示的数25. 甲、乙两所幼儿园计划在“元旦”一起举办文艺汇演活动,已知甲、乙两所幼儿园一共96人(其中甲幼儿园人数多于乙幼儿园人数,且甲幼儿园人数不足90人).现准备给每位小朋友都购买一套演出服装,服装厂给出如下价目表:
(1)、则点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长= (单位长度);(2)、若点P是线段BC的中点,则P点在数轴上表示的数是:(3)、若点Q是坐标轴上的点,且QC=2QB,则Q点在数轴上表示的数25. 甲、乙两所幼儿园计划在“元旦”一起举办文艺汇演活动,已知甲、乙两所幼儿园一共96人(其中甲幼儿园人数多于乙幼儿园人数,且甲幼儿园人数不足90人).现准备给每位小朋友都购买一套演出服装,服装厂给出如下价目表:购买服装的套数
48套以下
48套至90套
91套及以上
每套服装的价格
65元
55元
45元
如果两所幼儿园分别单独购买服装,一共应付5680元.
(1)、如果甲、乙两所幼儿园联合起来购买服装,那么比各自购买服装共可以节省多少钱?(2)、甲、乙两所幼儿园各有多少名小朋友准备参加演出?(3)、如果甲幼儿园有10名小朋友因为校外活动不能参加演出,那么你有几种购买方案?通过比较,你认为如何购买服装才能最省钱?26. 用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
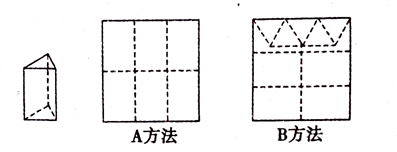
现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)、用x的代数式分别表示裁剪出的侧面和底面的个数;(2)、若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
-