湖北省武汉市洪山区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-23 类型:期末考试
一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
-
1. 下列运算正确的是( )A、 B、 C、 D、2. “致中和,天地位焉,万物育焉”.对称美是我国古人和谐平衡思想的体现,常被运用于建筑,器物,绘画,标识等作品的设计上,使对称之美惊艳了千年.下列大学校徽的主体图案不是轴对称图形的是( )A、武汉理工大学
 B、华中师范大学
B、华中师范大学 C、华中农业大学
C、华中农业大学 D、武汉大学
D、武汉大学 3. 下列式子中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 下列等式成立的是( )A、 B、 C、 D、5. 如果把中的和都扩大为原来的5倍,那么分式的值( )A、扩大为原来的4倍 B、不变 C、缩小为原来的 D、扩大为原来的5倍6. 若且 , 则分式的值是( )A、 B、2 C、 D、7. △ABC的三边a,b,c满足a2+b2+c2=ab+bc+ac,则△ABC是( )A、等边三角形 B、腰底不等的等边三角形 C、直角三角形 D、等腰直角三角形8. 如图,中, , 点D是边上一点,连接 , 将沿所在直线折叠得到 , 点F是点A的对应点,与交于点E,下列结论一定正确的是( )
3. 下列式子中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 下列等式成立的是( )A、 B、 C、 D、5. 如果把中的和都扩大为原来的5倍,那么分式的值( )A、扩大为原来的4倍 B、不变 C、缩小为原来的 D、扩大为原来的5倍6. 若且 , 则分式的值是( )A、 B、2 C、 D、7. △ABC的三边a,b,c满足a2+b2+c2=ab+bc+ac,则△ABC是( )A、等边三角形 B、腰底不等的等边三角形 C、直角三角形 D、等腰直角三角形8. 如图,中, , 点D是边上一点,连接 , 将沿所在直线折叠得到 , 点F是点A的对应点,与交于点E,下列结论一定正确的是( )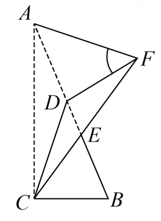 A、 B、 C、 D、9. 已知实数满足 , 则代数式的值为( )A、9 B、7 C、0 D、10. 如图,在中,以 , 为腰作等腰直角和等腰直角 , 其中 , 连接 , 为边上的高,延长交于点 . 有下列结论:①;②;③;④为中点.
A、 B、 C、 D、9. 已知实数满足 , 则代数式的值为( )A、9 B、7 C、0 D、10. 如图,在中,以 , 为腰作等腰直角和等腰直角 , 其中 , 连接 , 为边上的高,延长交于点 . 有下列结论:①;②;③;④为中点.其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(共6小题,每小题3分,共18分)
-
11. 当x时,分式 的值为零.12. 化简: .13. 已知 , 则 的值为 .14. 已知是完全平方式,则常数 .15. 已知关于的分式方程的解是正数,则的取值范围是 .16. 如图,等腰直角中, , , 为中点.点为射线上的一个动点,以为直角边向右上方构造等腰直角 , , 连接 . 在点的运动过程中,长度的最小值是 .

三、解答题(共8小题,共72分)在答题卡指定的位置上写出必要的演算过程或证明过程.
-
17. 因式分解:(1)、(2)、18. 如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 .
 (1)、求证: ;(2)、若 , ,求 的度数.19. 先化简,再求值: ,从 ,1,2,3中选择一个合适的数代入并求值.20. 探索(1)、如果 , 则;(2)、如果 , 则;(3)、总结如果(其中为常数),则;(4)、应用若代数式的值为整数,求满足条件的整数的值.21. 如图,在网格中,每个小正方形边长为1个单位长度,我们把每个小正方形的顶点称为格点,均为格点,请按要求仅用一把无刻度的直尺作图,画图过程用虚线表示,画图结果用实线表示.
(1)、求证: ;(2)、若 , ,求 的度数.19. 先化简,再求值: ,从 ,1,2,3中选择一个合适的数代入并求值.20. 探索(1)、如果 , 则;(2)、如果 , 则;(3)、总结如果(其中为常数),则;(4)、应用若代数式的值为整数,求满足条件的整数的值.21. 如图,在网格中,每个小正方形边长为1个单位长度,我们把每个小正方形的顶点称为格点,均为格点,请按要求仅用一把无刻度的直尺作图,画图过程用虚线表示,画图结果用实线表示. (1)、在图1中,作(D在下方),且;(2)、在图1中;作的中点 , 在线段上作点 , 使得;(3)、在图2中;在线段上作点 , 使得;(4)、在图2中,已知 , 在上作点 , 使得 .22. 有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.(1)、求甲、乙两工程队每天各完成多少米?(2)、如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲、乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可合作施工多少天?(注:工作天数取整数)23. 如图
(1)、在图1中,作(D在下方),且;(2)、在图1中;作的中点 , 在线段上作点 , 使得;(3)、在图2中;在线段上作点 , 使得;(4)、在图2中,已知 , 在上作点 , 使得 .22. 有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.(1)、求甲、乙两工程队每天各完成多少米?(2)、如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲、乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可合作施工多少天?(注:工作天数取整数)23. 如图 (1)、如图1,中, , 平分交于 , 过点作的垂线交的垂直平分线于M,连AM,N在的延长线上.求证:平分;(2)、把(1)中的“平分交手”换成“平分的外角交直线于D”,其他条件不变,请在图2中补全图形,并直接写出的度数 ▲ ;(用含的式子表示)(3)、在(1)的条件下;若(如图3),且 , 作于 , 求的长度.24. 在平面直角坐标系中, , , 且 .
(1)、如图1,中, , 平分交于 , 过点作的垂线交的垂直平分线于M,连AM,N在的延长线上.求证:平分;(2)、把(1)中的“平分交手”换成“平分的外角交直线于D”,其他条件不变,请在图2中补全图形,并直接写出的度数 ▲ ;(用含的式子表示)(3)、在(1)的条件下;若(如图3),且 , 作于 , 求的长度.24. 在平面直角坐标系中, , , 且 . (1)、直接写出两点的坐标;(2)、如图1,点在线段上,且点横坐标为 , 连接 . 在第四象限过点作 , 且 , 连接 , 作于 , 交于点 , 求的面积;(3)、如图2, , 与轴非负半轴重合,在第一象限,将以/秒的速度绕点在第一象限内逆时针旋转, , 分别与线段交于点 , , 在第二象限过点作 , 且 , 问经过多长时间,为等腰三角形?
(1)、直接写出两点的坐标;(2)、如图1,点在线段上,且点横坐标为 , 连接 . 在第四象限过点作 , 且 , 连接 , 作于 , 交于点 , 求的面积;(3)、如图2, , 与轴非负半轴重合,在第一象限,将以/秒的速度绕点在第一象限内逆时针旋转, , 分别与线段交于点 , , 在第二象限过点作 , 且 , 问经过多长时间,为等腰三角形?